So führen sie eine hierarchische regression in stata durch

Die hierarchische Regression ist eine Technik, mit der wir mehrere verschiedene lineare Modelle vergleichen können.

Die Grundidee besteht darin, dass wir zunächst ein lineares Regressionsmodell mit einer einzelnen erklärenden Variablen anpassen. Als nächstes passen wir ein weiteres Regressionsmodell unter Verwendung einer zusätzlichen erklärenden Variablen an. Wenn das R-Quadrat (der Anteil der Varianz in der Antwortvariablen, der durch die erklärenden Variablen erklärt werden kann) im zweiten Modell deutlich höher ist als das R-Quadrat im vorherigen Modell, bedeutet dies, dass das zweite Modell besser ist.

Anschließend wiederholen wir den Prozess der Anpassung zusätzlicher Regressionsmodelle mit mehr erklärenden Variablen und prüfen, ob die neueren Modelle eine Verbesserung gegenüber den vorherigen Modellen bieten.

Dieses Tutorial bietet ein Beispiel für die Durchführung einer hierarchischen Regression in Stata.

Beispiel: hierarchische Regression in Stata

Wir werden einen integrierten Datensatz namens auto verwenden, um zu veranschaulichen, wie eine hierarchische Regression in Stata durchgeführt wird. Laden Sie zunächst den Datensatz, indem Sie Folgendes in das Befehlsfeld eingeben:

automatische Nutzung des Systems

Mit dem folgenden Befehl können wir eine schnelle Zusammenfassung der Daten erhalten:

zusammenfassen

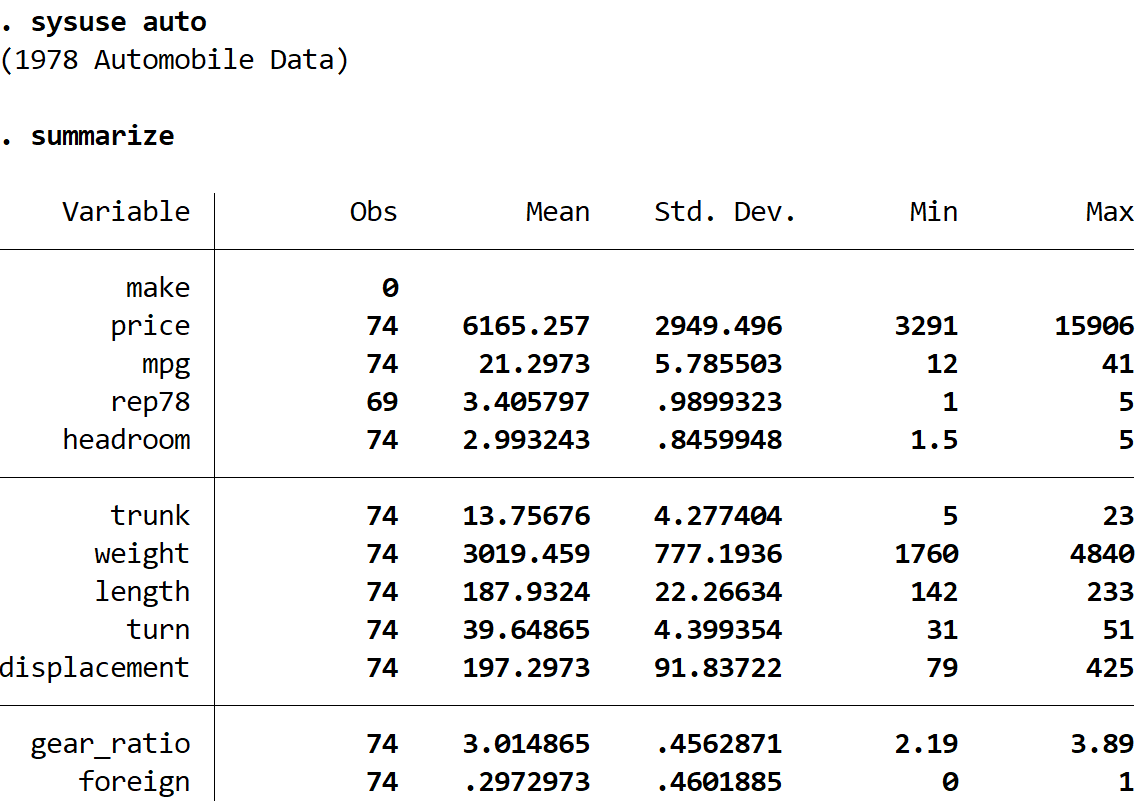
Wir können sehen, dass der Datensatz Informationen zu 12 verschiedenen Variablen für insgesamt 74 Autos enthält.

Wir passen die folgenden drei linearen Regressionsmodelle an und verwenden die hierarchische Regression, um zu sehen, ob jedes nachfolgende Modell eine signifikante Verbesserung gegenüber dem vorherigen Modell bietet oder nicht:

Modell 1: Preis = Intercept + mpg

Modell 2: Preis = Intercept + mpg + Gewicht

Modell 3: Preis = Intercept + mpg + Gewicht + Übersetzungsverhältnis

Um eine hierarchische Regression in Stata durchzuführen, müssen wir zunächst das Hireg- Paket installieren. Geben Sie dazu Folgendes in das Befehlsfeld ein:

Finde Hireg

Klicken Sie im angezeigten Fenster auf Hireg von https://fmwww.bc.edu/RePEc/bocode/h

Klicken Sie im nächsten Fenster auf den Link „Klicken Sie hier, um zu installieren“ .

Das Paket wird in Sekundenschnelle installiert. Um dann eine hierarchische Regression durchzuführen, verwenden wir den folgenden Befehl:

Mietpreis (mpg) (Gewicht) (Getriebeverhältnis)

Folgendes wird von Stata verlangt:

• Führen Sie in jedem Modell eine hierarchische Regression durch, wobei der Preis als Antwortvariable verwendet wird.
• Verwenden Sie für das erste Modell mpg als erklärende Variable.
• Fügen Sie für das zweite Modell Gewicht als zusätzliche erklärende Variable hinzu.
• Fügen Sie für das dritte Modell gear_ratio als weitere erklärende Variable hinzu.

Hier ist das Ergebnis des ersten Modells:

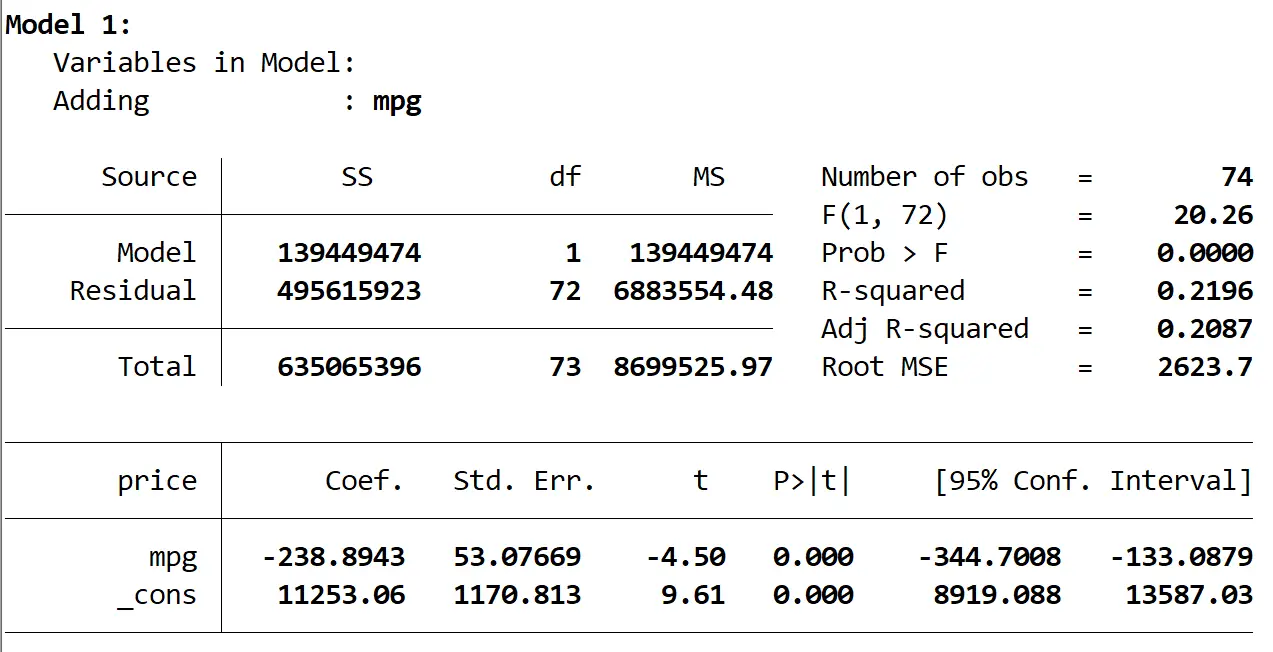
Wir sehen, dass das R-Quadrat des Modells 0,2196 beträgt und der Gesamt-p-Wert (Prob > F) des Modells 0,0000 beträgt, was bei α = 0,05 statistisch signifikant ist.

Als nächstes sehen wir das Ergebnis des zweiten Modells:

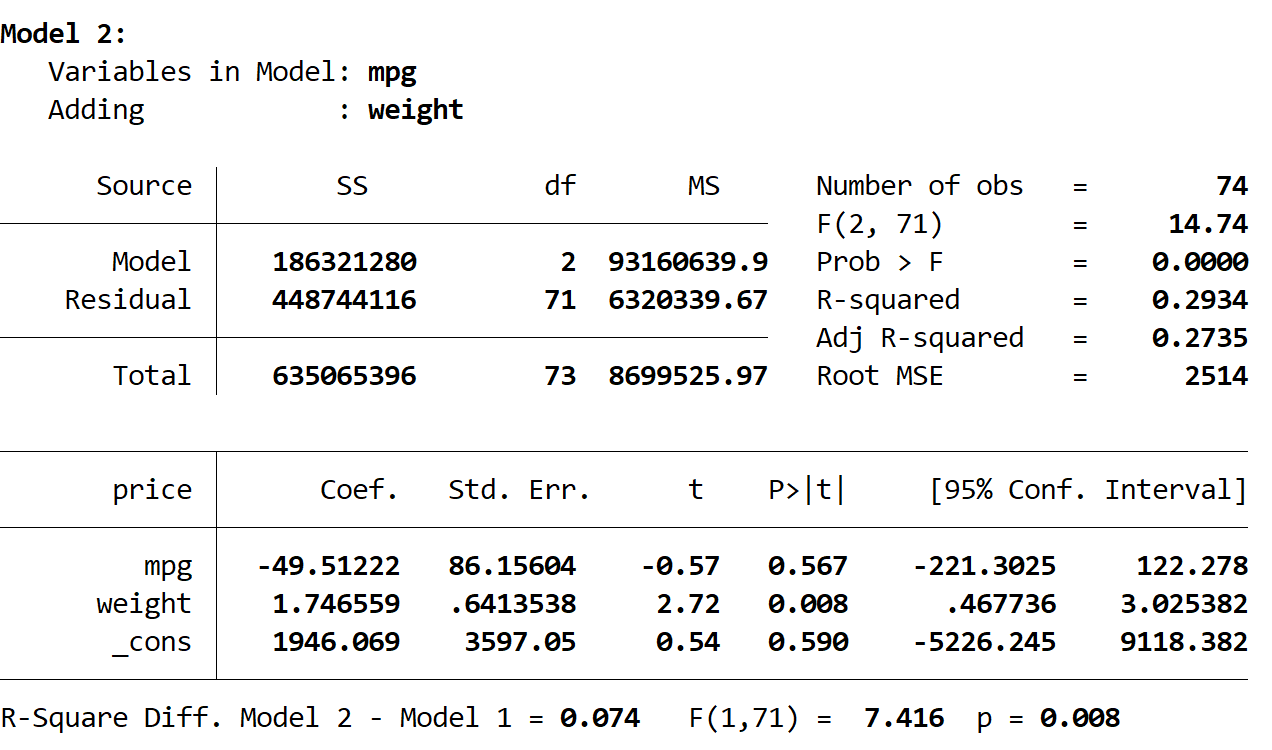
Das R-Quadrat dieses Modells beträgt 0,2934 und ist damit größer als das des ersten Modells. Um festzustellen, ob dieser Unterschied statistisch signifikant ist, führte Stata einen F-Test durch, der am Ende des Ergebnisses die folgenden Zahlen ergab:

• R-Quadrat-Differenz zwischen den beiden Modellen = 0,074
• F-Statistik für Differenz = 7,416
• Entsprechender p-Wert der F-Statistik = 0,008

Da der p-Wert kleiner als 0,05 ist, kommen wir zu dem Schluss, dass das zweite Modell im Vergleich zum ersten Modell eine statistisch signifikante Verbesserung aufweist.

Schließlich können wir das Ergebnis des dritten Modells sehen:

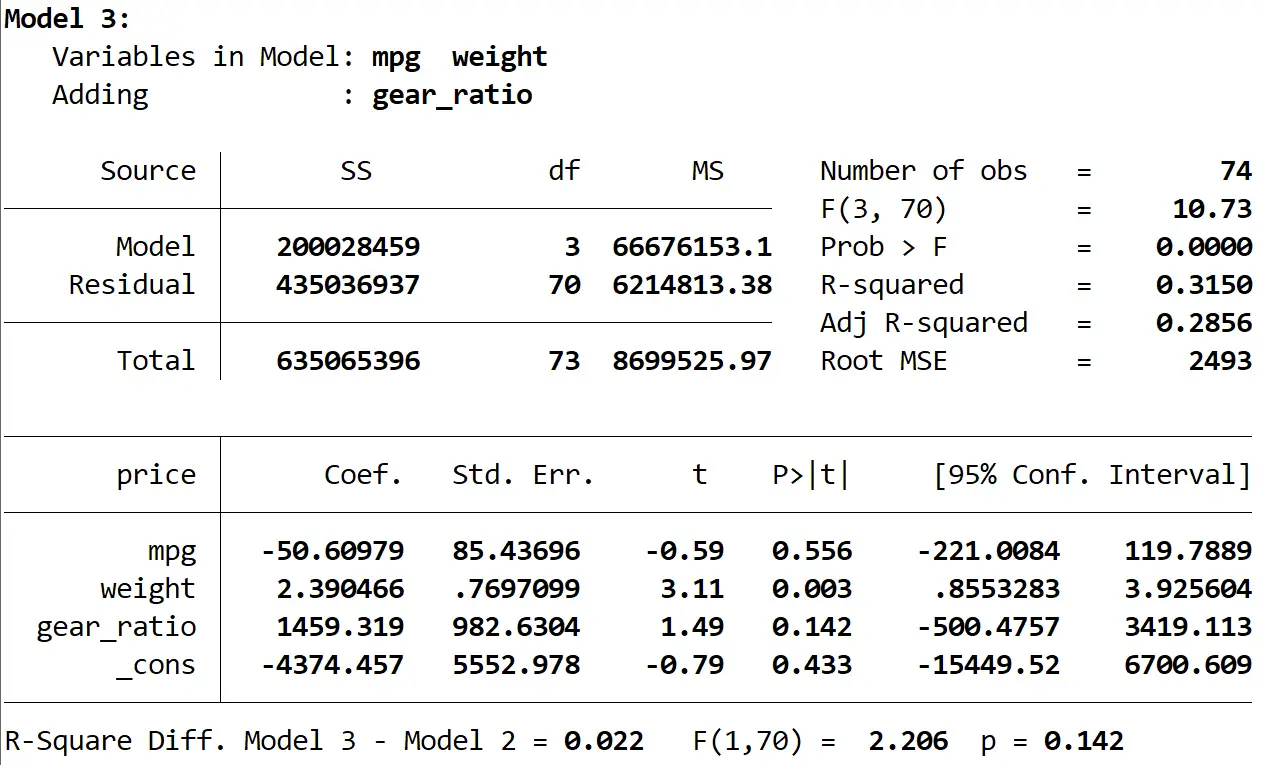
Das R-Quadrat dieses Modells beträgt 0,3150 und ist damit größer als das des zweiten Modells. Um festzustellen, ob dieser Unterschied statistisch signifikant ist, führte Stata einen F-Test durch, der am Ende des Ergebnisses die folgenden Zahlen ergab:

• R-Quadrat-Differenz zwischen den beiden Modellen = 0,022
• F-Statistik für Differenz = 2,206
• Entsprechender p-Wert der F-Statistik = 0,142

Da der p-Wert nicht weniger als 0,05 beträgt, haben wir keine ausreichenden Beweise dafür, dass das dritte Modell eine Verbesserung gegenüber dem zweiten Modell bietet.

Ganz am Ende des Ergebnisses können wir sehen, dass Stata eine Zusammenfassung der Ergebnisse bereitstellt:

In diesem speziellen Beispiel würden wir zu dem Schluss kommen, dass Modell 2 eine signifikante Verbesserung gegenüber Modell 1 bot, Modell 3 jedoch keine signifikante Verbesserung gegenüber Modell 2.