Posterior-wahrscheinlichkeit: definition + beispiel

Die A- posteriori-Wahrscheinlichkeit ist die aktualisierte Wahrscheinlichkeit, dass ein Ereignis unter Berücksichtigung neuer Informationen eintritt.

Beispielsweise könnten wir an der Wahrscheinlichkeit interessiert sein, mit der ein Ereignis „A“ eintritt, nachdem ein Ereignis „B“ berücksichtigt wurde, das gerade eingetreten ist. Wir könnten diese A-posteriori-Wahrscheinlichkeit mit der folgenden Formel berechnen:

P(A|B) = P(A) * P(B|A) / P(B)

Gold:

P(A|B) = die Wahrscheinlichkeit, dass Ereignis A eintritt, vorausgesetzt, Ereignis B ist eingetreten. Beachten Sie, dass „| » bedeutet „gegeben“.

P(A) = die Wahrscheinlichkeit, dass Ereignis A eintritt.

P(B) = die Wahrscheinlichkeit, dass Ereignis B eintritt.

P(B|A) = die Wahrscheinlichkeit, dass Ereignis B eintritt, vorausgesetzt, Ereignis A ist eingetreten.

Beispiel: Berechnung der A-posteriori-Wahrscheinlichkeit

Ein Wald besteht zu 20 % aus Eichen und zu 80 % aus Ahornen. Nehmen wir an, wir wissen, dass 90 % der Eichen gesund sind, während nur 50 % der Ahornbäume gesund sind. Angenommen, Sie können aus der Ferne erkennen, dass ein bestimmter Baum gesund ist. Wie groß ist die Wahrscheinlichkeit, dass es sich bei dem Baum um eine Eiche handelt?

Denken Sie daran, dass die Wahrscheinlichkeit, dass Ereignis A eintritt, wenn Ereignis B eingetreten ist, wie folgt ist:

P(A|B) = P(A) * P(B|A) / P(B)

In diesem Beispiel beträgt die Wahrscheinlichkeit, dass es sich bei dem Baum um eine Eiche handelt, sofern der Baum gesund ist:

P(Eiche|Gesund) = P(Eiche) * P(Gesund|Eiche) / P(Gesund)

P(Eiche) = Die Wahrscheinlichkeit, dass ein gegebener Baum eine Eiche ist, beträgt 0,2 , da 20 % aller Bäume im Wald Eichen sind.

P(Gesund) = Die Wahrscheinlichkeit, dass ein gegebener Baum gesund ist, kann wie folgt berechnet werden: (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Gesund|Eiche) = Die Wahrscheinlichkeit, dass ein Baum gesund ist, wenn man davon ausgeht, dass es sich um eine Eiche handelt, beträgt 0,9 , da uns gesagt wurde, dass 90 % der Eichen gesund sind.

Mithilfe dieser drei Zahlen können wir die Wahrscheinlichkeit ermitteln, dass es sich bei dem Baum um eine Eiche handelt, sofern er gesund ist:

P(Eiche|Gesund) = P(Eiche) * P(Gesund|Eiche) / P(Gesund) = (0,2) * (0,9) / (0,58) = 0,3103 .

Für ein intuitives Verständnis dieser Wahrscheinlichkeit nehmen wir an, dass das folgende Raster diesen Wald aus 100 Bäumen darstellt. Genau 20 der Bäume sind Eichen und 18 davon sind gesund. Die anderen 80 Bäume sind Ahornbäume und 40 davon sind gesund.

(O = Eiche, M = Ahorn, Grün = Gesund, Rot = Ungesund)

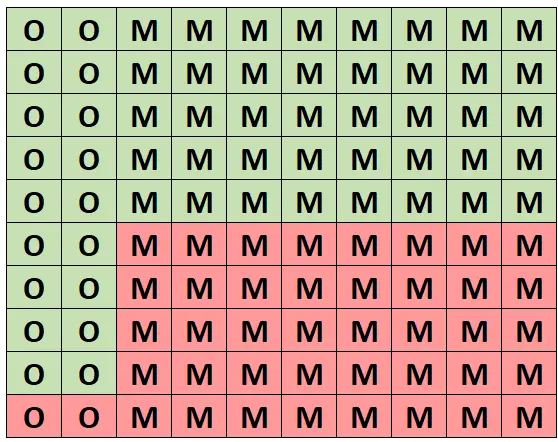
Von allen Bäumen sind genau 58 gesund und 18 dieser gesunden Bäume sind Eichen. Wenn wir also wissen, dass wir einen gesunden Baum ausgewählt haben, beträgt die Wahrscheinlichkeit, dass es sich um eine Eiche handelt, 18/58 = 0,3103 .

Wann sollten Sie die Posterior-Wahrscheinlichkeit verwenden?

Die Posterior-Wahrscheinlichkeit wird in einer Vielzahl von Bereichen verwendet, darunter im Finanzwesen, in der Medizin, in der Wirtschaft und in der Wettervorhersage.

Der Zweck der Verwendung von Posterior-Wahrscheinlichkeiten besteht darin, eine frühere Überzeugung, die wir über etwas hatten, zu aktualisieren, sobald wir neue Informationen erhalten.

Erinnern Sie sich an das vorherige Beispiel: Wir wussten, dass die Wahrscheinlichkeit, dass es sich bei einem bestimmten Baum im Wald um eine Eiche handelte, 20 % betrug. Dies wird als A- priori-Wahrscheinlichkeit bezeichnet. Wenn wir einfach einen Baum zufällig auswählen würden, wüssten wir, dass die Wahrscheinlichkeit, dass es sich um eine Eiche handelt, 0,20 beträgt.

Als wir jedoch die neue Information erhielten, dass der von uns ausgewählte Baum gesund war, konnten wir anhand dieser neuen Informationen ermitteln, dass die A-posteriori-Wahrscheinlichkeit , dass es sich bei diesem Baum um eine Eiche handelt, stattdessen bei 0,3103 lag.

In der realen Welt entdecken Menschen ständig neue Informationen. Diese neuen Informationen helfen uns, unsere bisherigen Überzeugungen zu aktualisieren. Statistisch gesehen bedeutet dies, dass wir in der Lage sind, A-Posteriori-Wahrscheinlichkeiten für eintretende Ereignisse zu generieren, was uns hilft, ein genaueres Verständnis der Welt zu erlangen und genauere Vorhersagen über zukünftige Ereignisse zu treffen.