So vergleichen sie histogramme (mit beispielen)

Ein Histogramm ist eine Art Diagramm, mit dem wir die Verteilung von Werten in einem Datensatz visualisieren können.

Die X-Achse zeigt die Werte des Datensatzes und die Y-Achse zeigt die Häufigkeit jedes Werts.

Histogramme sind nützlich, weil sie es uns ermöglichen, die Verteilung von Werten in einem Datensatz schnell zu verstehen. Sie eignen sich auch zum Vergleich zweier unterschiedlicher Datensätze.

Wenn wir zwei oder mehr Histogramme vergleichen, können wir drei verschiedene Fragen beantworten:

1. Wie vergleichen sich die Medianwerte?

Wir können grob abschätzen, dass der Median in der Nähe der Mitte jedes Histogramms liegt, sodass wir die Medianwerte der Verteilungen vergleichen können.

2. Wie ist die Streuung im Vergleich?

Wir können visuell erkennen, welches Histogramm stärker gestreut ist, was uns eine Vorstellung davon gibt, welche Verteilung stärker gestreute Werte aufweist.

3. Wie lässt sich Asymmetrie vergleichen?

Wenn ein Histogramm auf der linken Seite des Diagramms einen „Schwanz“ aufweist, spricht man von einer negativen Schiefe. Wenn umgekehrt ein Histogramm einen „Schwanz“ auf der rechten Seite des Diagramms aufweist, spricht man von einer positiven Schiefe. Wir können jedes Histogramm visuell überprüfen, um die Schiefe zu vergleichen.

Das folgende Beispiel zeigt, wie man zwei verschiedene Histogramme vergleicht und diese drei Fragen beantwortet.

Beispiel: Vergleich von Histogrammen

Angenommen, 200 Studenten verwenden eine Lernmethode, um sich auf eine Prüfung vorzubereiten, und weitere 200 Studenten verwenden eine andere Lernmethode, um sich auf dieselbe Prüfung vorzubereiten.

Angenommen, wir erstellen die folgenden Histogramme, um die Prüfungsergebnisse jeder Studentengruppe zu vergleichen:

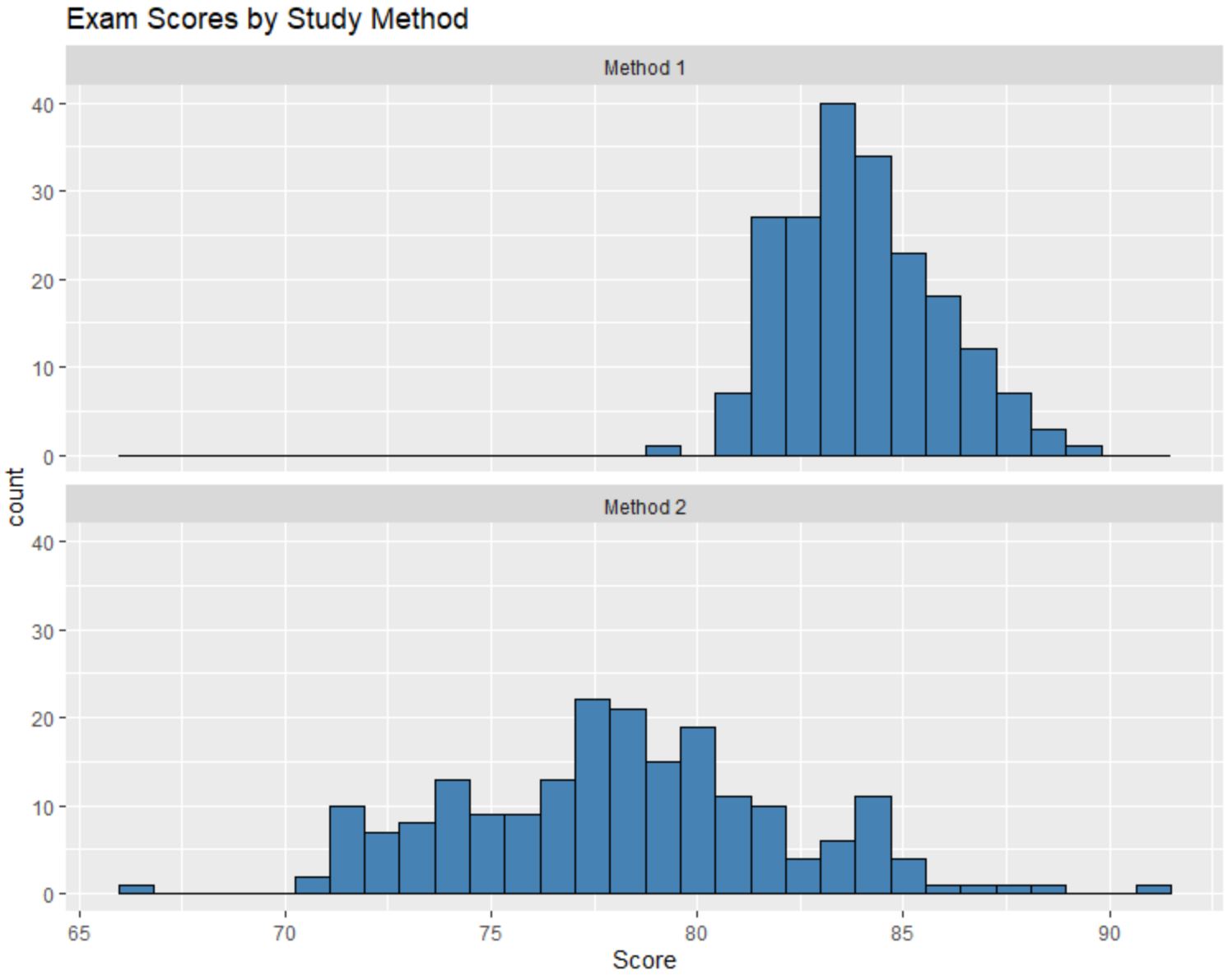
Wir können diese Histogramme vergleichen und die folgenden drei Fragen beantworten:

1. Wie vergleichen sich die Medianwerte?

Obwohl wir die genauen Medianwerte jeder Verteilung nicht allein durch die Betrachtung der Histogramme kennen, ist es offensichtlich, dass die mittlere Prüfungspunktzahl der Schüler, die Methode 1 verwendet haben, höher ist als die mittlere Prüfungspunktzahl der Schüler, die Methode 1 verwendet haben Methode 2 .

Wir könnten schätzen, dass der Medianwert für Methode 1 bei etwa 84 und der Medianwert für Methode 2 bei etwa 78 liegt.

2. Wie ist die Streuung im Vergleich?

Die Histogrammwerte für Methode 2 sind viel stärker gestreut als die für Methode 1, was uns zeigt, dass die Prüfungsergebnisse für Studenten, die Methode 2 verwendet haben, viel stärker gestreut sind.

3. Wie lässt sich Asymmetrie vergleichen?

Ein Blick auf die Histogramme zeigt, dass die Verteilung der Testergebnisse für Methode 1 leicht nach rechts verschoben ist, was durch den „Schwanz“ angezeigt wird, der sich rechts vom Histogramm erstreckt.

Es scheint jedoch keinen „Schwanz“ in der Verteilung der Prüfungsergebnisse für Methode 2 zu geben, was darauf hindeutet, dass die Verteilung wenig oder nicht schief ist.

Bonus : Hier ist der Code, den wir in R verwendet haben, um diese beiden Histogramme zu erstellen:

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben mit Histogrammen ausführen:

So schätzen Sie den Mittelwert und den Median eines beliebigen Histogramms
So schätzen Sie die Standardabweichung eines beliebigen Histogramms ein
So beschreiben Sie die Form von Histogrammen