Homoskedastizität

Dieser Artikel erklärt, was Homoskedastizität in der Statistik ist. Sie finden also die Definition von Homoskedastizität, die Ursachen dafür, dass ein Regressionsmodell keine Homoskedastizität aufweist, und darüber hinaus, wie man das Problem beheben kann.

Was ist Homoskedastizität?

Homoskedastizität ist ein Merkmal eines Regressionsmodells, dessen Fehler der erklärenden Variablen eine konstante Varianz aufweisen. Das heißt, wenn die Fehlervarianz eines Regressionsmodells konstant ist, weist das besagte Modell Homoskedastizität auf und ist daher ein homoskedastisches Modell.

Denken Sie daran, dass der Fehler (oder das Residuum) als die Differenz zwischen dem tatsächlichen Wert und dem vom Regressionsmodell geschätzten Wert definiert ist.

Wenn wir ein Regressionsmodell ausführen, erhalten wir für jede Beobachtung einen anderen Wert als im vorherigen Ausdruck. Ein homoskedastisches statistisches Modell ist also ein Modell, bei dem die Varianz der berechneten Fehler über die gesamten Beobachtungen hinweg konstant ist.

Es ist wichtig, dass ein Regressionsmodell Homoskedastizität aufweist; Tatsächlich ist dies eine der vorherigen Annahmen von Regressionsmodellen. Wenn die Residuen nicht homoskedastisch sind, ist es besser, das Modell auf andere Weise zu wiederholen, um Homoskedastizität zu erhalten. Andernfalls ist es wahrscheinlich, dass die Schätzung der Regressionskoeffizienten fehlerhaft ist, und es kommt auch zu Fehlern beim Hypothesentest, wenn Nullhypothesen akzeptiert werden, die eigentlich verworfen werden sollten.

Ursachen für mangelnde Homoskedastizität

Die häufigsten Ursachen dafür, dass ein Modell keine Homoskedastizität aufweist, sind:

• Wenn der Datenbereich im Vergleich zum Durchschnitt sehr groß ist. Wenn in derselben statistischen Stichprobe sehr große und sehr kleine Werte vorhanden sind, ist das erhaltene Regressionsmodell wahrscheinlich nicht homoskedastisch.
• Auch das Weglassen von Variablen im Regressionsmodell führt zu einem Mangel an Homoskedastizität. Wenn eine relevante Variable nicht im Modell enthalten ist, wird ihre Variation logischerweise in die Residuen einbezogen und nicht unbedingt behoben.
• Eine Änderung der Struktur kann zu einer schlechten Anpassung des Modells an den Datensatz führen und daher ist die Varianz der Residuen nicht konstant.
• Wenn einige Variablen viel größere Werte als die anderen erklärenden Variablen haben, weist das Modell möglicherweise keine Homoskedastizität auf. In diesem Fall können die Variablen relativiert werden, um das Problem zu lösen.

Es gibt jedoch einige Fälle, die von Natur aus schwer als Homoskedastizität darzustellen sind. Wenn wir beispielsweise das Einkommen einer Person anhand ihrer Lebensmittelausgaben modellieren, weisen wohlhabendere Menschen eine viel größere Variabilität ihrer Lebensmittelausgaben auf als ärmere Menschen. Denn ein reicher Mensch isst manchmal in teuren Restaurants und ein anderes Mal in billigen Restaurants, im Gegensatz zu einem armen Menschen, der immer in billigen Restaurants isst. Daher ist es schwierig, im Regressionsmodell Homoskedastizität zu erreichen.

Daten korrigieren, um Homoskedastizität zu erreichen

Wenn das erhaltene Regressionsmodell nicht homoskedastisch ist, können die folgenden Korrekturen versucht werden, um Homoskedastizität zu erreichen:

• Berechnen Sie den natürlichen Logarithmus der unabhängigen Variablen. Dies ist im Allgemeinen nützlich, wenn die Varianz der Residuen im Diagramm zunimmt.
• Abhängig vom Residuendiagramm kann eine andere Art der Transformation der unabhängigen Variablen praktischer sein. Wenn der Graph beispielsweise die Form einer Parabel hat, können wir das Quadrat der unabhängigen Variablen berechnen und diese Variable zum Modell hinzufügen.
• Für das Modell können auch andere Variablen verwendet werden; Durch Entfernen oder Hinzufügen einer Variablen kann die Varianz der Residuen geändert werden.
• Anstelle des Kriteriums der kleinsten Quadrate kann auch das gewichtete Kriterium der kleinsten Quadrate verwendet werden.

Homoskedastizität und Heteroskedastizität

Abschließend werden wir sehen, was der Unterschied zwischen Homoskedastizität und Heteroskedastizität ist, da es sich um zwei wichtige statistische Konzepte von Regressionsmodellen handelt.

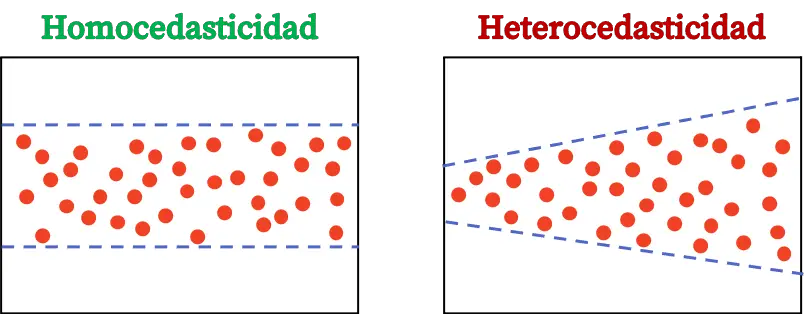
Heteroskedastizität ist ein statistisches Merkmal, das impliziert, dass die Residuen des Regressionsmodells keine konstante Varianz aufweisen, sodass die Variabilität der Fehler im gesamten Diagramm nicht gleich ist.

Der Unterschied zwischen Homoskedastizität und Heteroskedastizität ist die Konstanz der Fehlervarianz. Homoskedastizität impliziert, dass die Fehlervarianz konstant ist, während Heteroskedastizität impliziert, dass die Fehlervarianz nicht konstant ist.