So verwenden sie die hypergeometrische verteilung in excel

Die hypergeometrische Verteilung beschreibt die Wahrscheinlichkeit, aus einer endlichen Population der Größe N , die K Objekte mit dieser Eigenschaft enthält, k Objekte mit einer bestimmten Eigenschaft in n Ziehungen ohne Ersatz auszuwählen.

Wenn eine Zufallsvariable X einer hypergeometrischen Verteilung folgt, kann die Wahrscheinlichkeit, k Objekte mit einem bestimmten Merkmal auszuwählen, mit der folgenden Formel ermittelt werden:

P(X=k) = _K C _k ( _NK C _nk ) / _N C _n

Gold:

• N: Bevölkerungsgröße
• K: Anzahl der Objekte in der Population mit einem bestimmten Merkmal
• n: Stichprobengröße
• k: Anzahl der Objekte im Beispiel mit einer bestimmten Funktionalität
• _K C _k : Anzahl der Kombinationen von K Dingen, die k gleichzeitig genommen werden

Um die Wahrscheinlichkeiten zu berechnen, die mit der hypergeometrischen Verteilung in Excel verknüpft sind, können wir die folgende Formel verwenden:

 =HYPGEOM.DIST(sample_s, number_sample, population_s, number_pop, cumulative)

Gold:

• sample_s : Anzahl der Erfolge in der Stichprobe
• number_sample : Stichprobengröße
• Population_s : Anzahl der Erfolge in der Population
• number_pop : Bevölkerungsgröße
• kumulativ : Ob die kumulative Verteilungsfunktion berechnet werden soll

Die folgenden Beispiele zeigen, wie diese Formel in der Praxis angewendet werden kann.

Beispiel 1: Karten aus einem Stapel auswählen

Es gibt 4 Damen in einem Standardkartenspiel mit 52 Karten. Angenommen, wir wählen zufällig eine Karte aus einem Stapel aus und wählen dann ohne Ersatz zufällig eine andere Karte aus dem Stapel aus. Wie groß ist die Wahrscheinlichkeit, dass beide Karten Damen sind?

Wir können die folgende Formel in Excel verwenden, um die Wahrscheinlichkeit zu berechnen, dass Karten Damen sind:

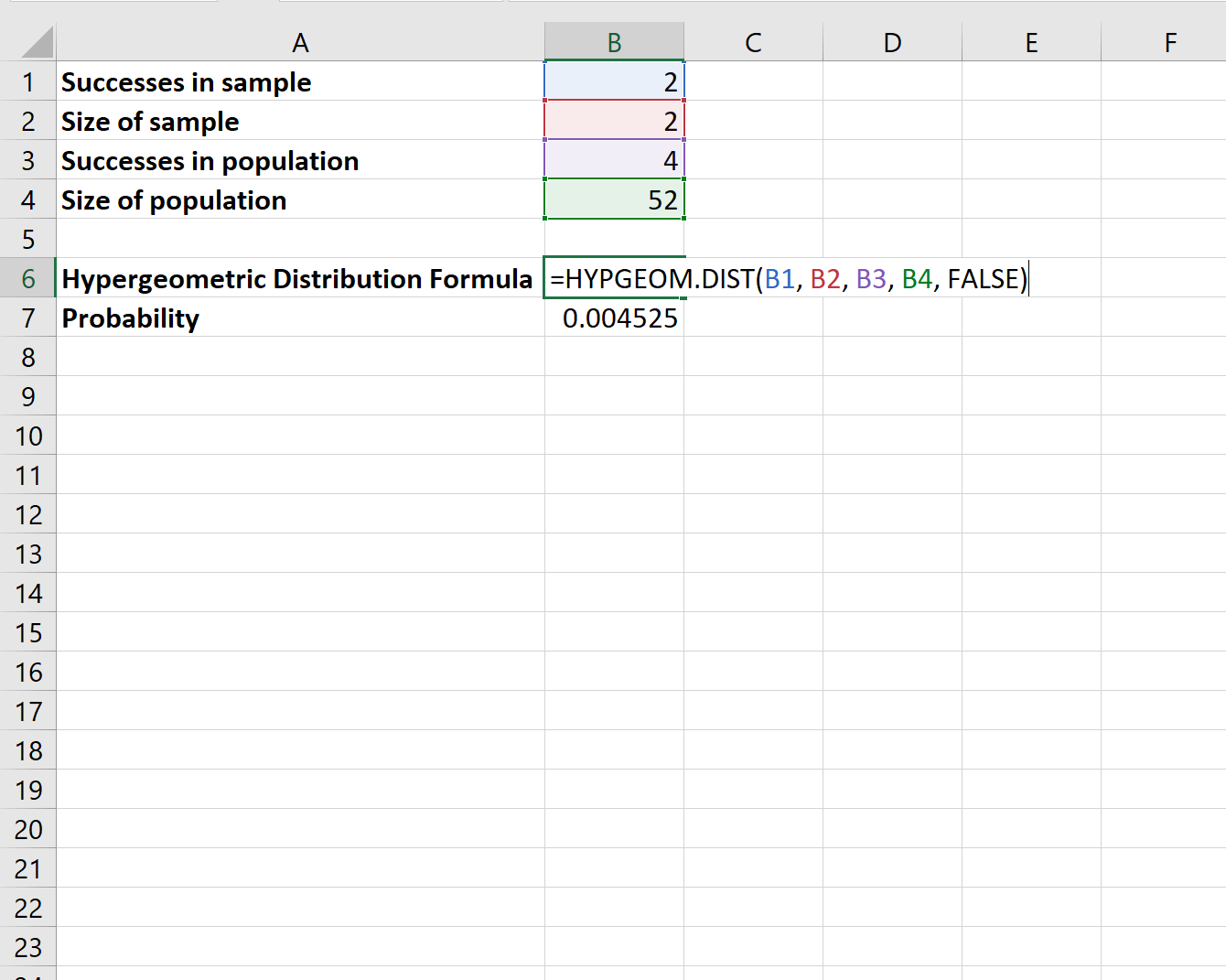
Die Wahrscheinlichkeit, dass beide Karten Damen sind, beträgt . 00452 .

Beispiel 2: Kugeln aus einer Urne sammeln

Eine Urne enthält 3 rote Kugeln und 5 grüne Kugeln. Sie wählen zufällig 4 Bälle aus. Wie groß ist die Wahrscheinlichkeit, dass Sie genau 2 rote Kugeln auswählen?

Um diese Wahrscheinlichkeit zu ermitteln, können wir in Excel die folgende Formel verwenden:

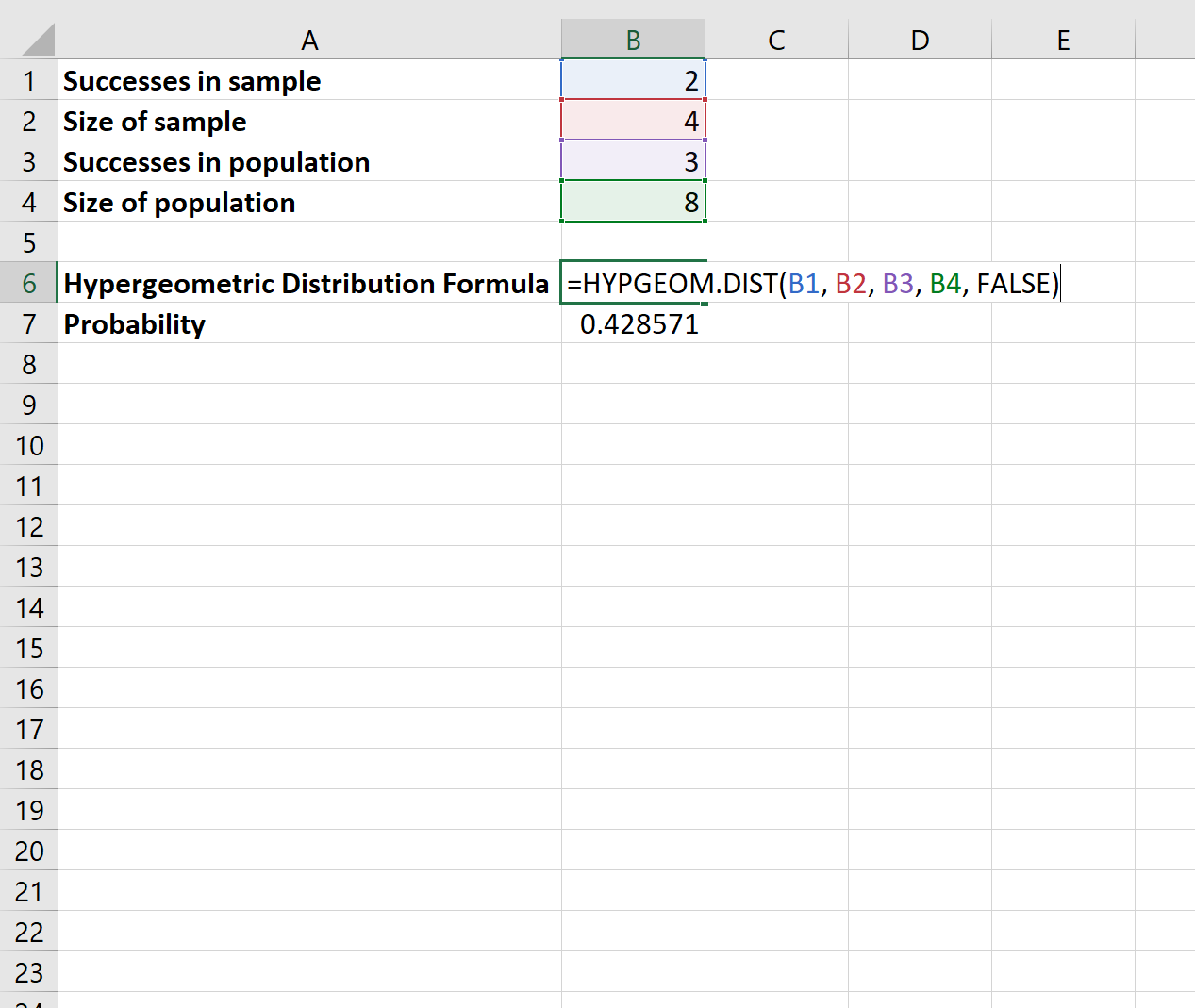
Die Wahrscheinlichkeit, dass Sie genau 2 rote Kugeln auswählen, beträgt . 428571 .

Beispiel 3: Murmeln aus einem Korb auswählen

Ein Korb enthält 7 lila Murmeln und 3 rosa Murmeln. Sie wählen zufällig 6 Murmeln aus. Wie groß ist die Wahrscheinlichkeit, dass Sie genau 3 rosa Murmeln auswählen?

Um diese Wahrscheinlichkeit zu ermitteln, können wir in Excel die folgende Formel verwenden:

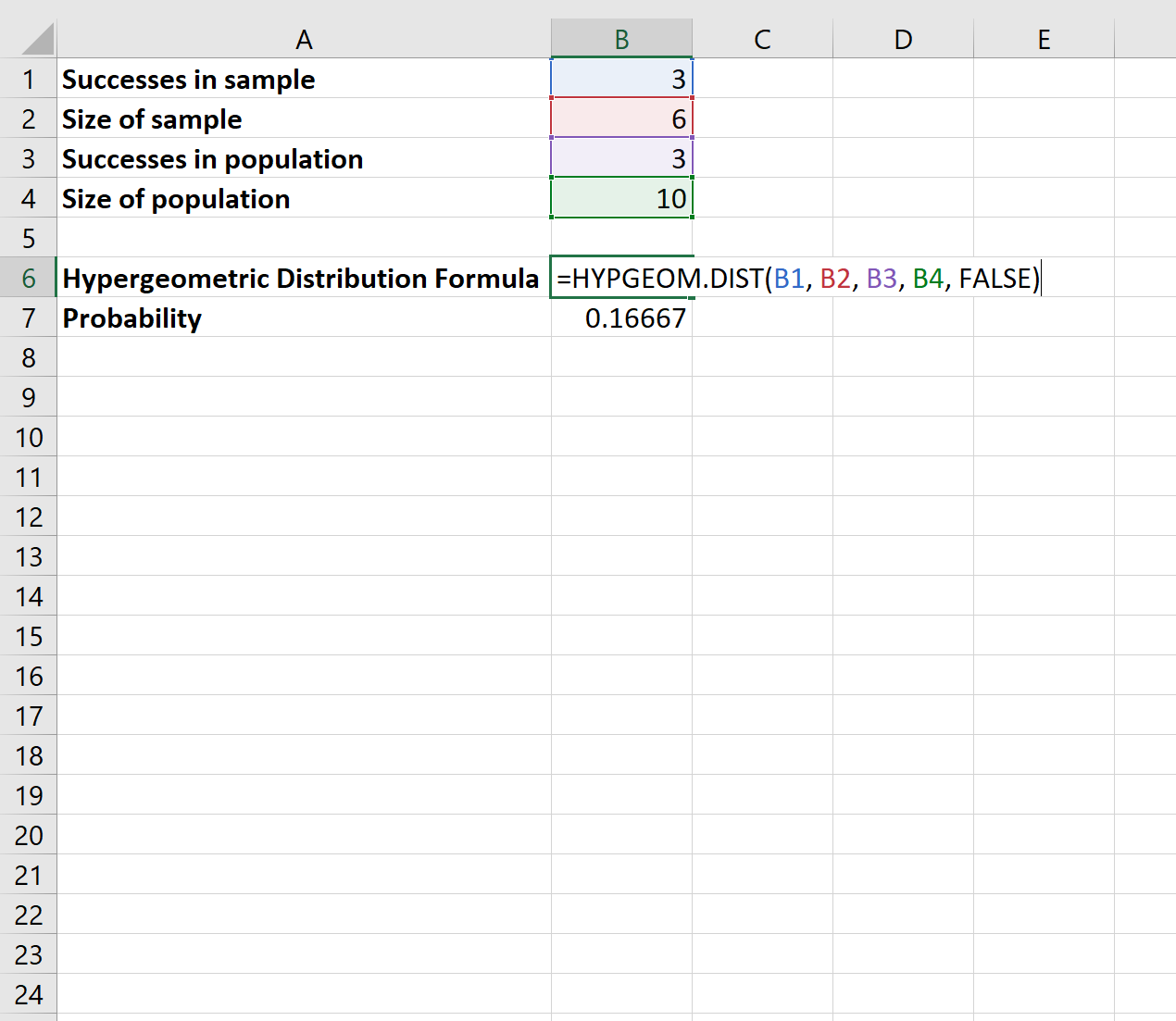
Die Wahrscheinlichkeit, dass Sie genau 3 rosa Murmeln auswählen, beträgt . 16667 .

Zusätzliche Ressourcen

Eine Einführung in die hypergeometrische Verteilung
Online-Rechner für hypergeometrische Verteilung