Hypothesentest auf varianz

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was ein Hypothesentest auf Varianz ist. So finden Sie die Formel zum Testen von Varianzhypothesen und zusätzlich eine Schritt-für-Schritt-Lösung.

Was ist ein Hypothesentest auf Varianz?

Der Hypothesentest auf Varianz ist eine statistische Methode, mit der bestimmt wird, ob die Nullhypothese einer Populationsvarianz abgelehnt werden soll oder nicht. Mit anderen Worten: Varianzhypothesentests werden verwendet, um die Hypothese über den Wert der Varianz einer Grundgesamtheit abzulehnen oder zu akzeptieren.

Konkret wird die Nullhypothese je nach Wert der Hypothesenteststatistik für Varianz und gewähltem Signifikanzniveau abgelehnt oder akzeptiert.

Bedenken Sie, dass Hypothesentests viele Namen haben. Man kann sie auch als Hypothesenkontraste, Hypothesentests oder Signifikanztests bezeichnen.

Hypothesentestformel für Varianz

Die Hypothesenteststatistik für die Varianz entspricht der Differenz zwischen der Stichprobengröße minus dem Einfachen der Stichprobenvarianz und dividiert durch den vorgeschlagenen Wert der Grundgesamtheitsvarianz. Die Hypothesenteststatistik für Varianz weist eine Chi-Quadrat-Verteilung auf.

Somit lautet die Formel zur Berechnung der Hypothesenteststatistik für die Varianz wie folgt:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Gold:

$\chi^2$

ist die Hypothesenteststatistik für Varianz, die eine Chi-Quadrat-Verteilung aufweist.
$n$

ist die Stichprobengröße.
$s^2$

ist die Stichprobenvarianz.
$\sigma^2$

ist die vorgeschlagene Populationsvarianz.

Um das Ergebnis der Statistik zu interpretieren, muss der erhaltene Wert mit dem kritischen Wert des Tests verglichen werden.

Wenn der Hypothesentest auf Varianz zweiseitig ist, wird die Nullhypothese abgelehnt, wenn die Statistik größer als der kritische Wert ist.
$\chi_{1-\alpha/2|n-1}^2$

oder wenn der kritische Wert kleiner ist als

$\chi_{\alpha/2|n-1}$

.
Wenn der Hypothesentest für die Varianz mit dem rechten Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn die Statistik größer als der kritische Wert ist
$\chi_{1-\alpha|n-1}^2$

.
Wenn der Hypothesentest auf Varianz mit dem linken Ende übereinstimmt, wird die Nullhypothese abgelehnt, wenn die Statistik kleiner als der kritische Wert ist
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Die kritischen Hypothesentestwerte für die Varianz werden aus der Chi-Quadrat-Verteilungstabelle ermittelt. Beachten Sie, dass die Freiheitsgrade für die Chi-Quadrat-Verteilung der Stichprobengröße minus 1 entsprechen.

Beispiel aus der Praxis für das Testen von Hypothesen auf Varianz

Nachdem wir die Definition des Varianzhypothesentests und seine Formel kennengelernt haben, sehen wir uns ein konkretes Beispiel an, um die Verinnerlichung des Konzepts abzuschließen.

Eine Fabrik verfügt über eine Maschine, die mit hoher Präzision Teile für ein Auto herstellt. Es besteht jedoch der Verdacht, dass man sich abgewandert hat und nun Teile mit einem Spalt von mehr als 8 mm ² fertigt. Um diese Hypothese zu widerlegen, wird eine Stichprobe von 25 Stück analysiert, deren Stichprobenvarianz 9,1 mm ² beträgt. Kann die Ausgangshypothese mit einem Signifikanzniveau α=0,05 verworfen werden?

Die Nullhypothese und die Alternativhypothese für diesen Varianzhypothesetest lauten wie folgt:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}“ title=“Rendered by QuickLaTeX.com“ height=“65″ width=“101″ style=“vertical-align: 0px;“> Um festzustellen, ob die Nullhypothese abgelehnt werden kann oder nicht, berechnen wir die Hypothesenteststatistik für die Varianz mithilfe der oben gezeigten Formel: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Wir suchen nun in der Chi-Quadrat-Verteilungstabelle nach dem kritischen Wert, der dem rechten Ende für 24 Freiheitsgrade und einem Signifikanzniveau α=0,05 entspricht:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Somit liegt die berechnete Statistik unter dem kritischen Wert des Tests und daher wird nicht die Nullhypothese des Varianzhypothesetests, sondern die Alternativhypothese abgelehnt.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Siehe: Hypothesentests für den Grundgesamtheitsmittelwert
➤ Siehe: Hypothesentest zum Bevölkerungsanteil

Hypothesentest auf Varianz zweier Populationen

Das Testen der Zwei-Population-Varianzhypothese wird verwendet, um die Hypothese abzulehnen oder zu akzeptieren, dass die Varianzen zweier verschiedener Populationen gleich sind.

Somit lautet die Nullhypothese eines Hypothesentests zur Varianz zweier Grundgesamtheiten immer wie folgt:

$H_0: \sigma^2_1=\sigma^2_2$

Und die Alternativhypothese kann eine von drei Optionen sein:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

In diesem Fall lautet die Formel zur Berechnung der Hypothesenteststatistik für die Varianz zweier Grundgesamtheiten:

$F=\cfrac{s_1^2}{s_2^2}$

Gold:

$F$

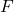
ist die Hypothesenteststatistik für die Varianz zweier Populationen, die einer F-Verteilung folgt.
$\sigma_1^2$

ist die Varianz der Grundgesamtheit 1.
$\sigma_2^2$

ist die Varianz der Grundgesamtheit 2.
$s_1^2$

ist die Varianz von Stichprobe 1.
$s_2^2$

ist die Varianz von Stichprobe 2.
$n_1$

ist Stichprobengröße 1.
$n_2$

ist Stichprobengröße 2.

Da die Snedecor-F-Verteilung nicht symmetrisch ist, wird die Nullhypothese basierend auf den folgenden Kriterien abgelehnt:

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{schwarz} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{schwarz} \ \text{If }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{schwarz} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{schwarz} \ \text{Si } F

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen