Hypothesentest auf mittelwertunterschiede

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was der Unterschied zwischen Mittelwerthypothesetests in der Statistik ist und wofür er verwendet wird. Ebenso erfahren Sie, wie Sie einen Hypothesentest zum Mittelwertunterschied durchführen und eine Schritt-für-Schritt-Übung lösen.

Was ist ein Hypothesentest für die Mittelwertdifferenz?

Der Hypothesentest auf Mittelwertunterschiede ist ein statistischer Test, der verwendet wird, um die Hypothese abzulehnen oder zu akzeptieren, dass die Mittelwerte zweier Grundgesamtheiten unterschiedlich sind. Das heißt, der Mittelwertdifferenz-Hypothesetest wird verwendet, um zu bestimmen, ob die Mittelwerte zweier Grundgesamtheiten gleich oder unterschiedlich sind.

Bedenken Sie, dass bei Hypothesentests getroffene Entscheidungen auf einem zuvor festgelegten Vertrauensniveau basieren. Daher kann nicht garantiert werden, dass das Ergebnis eines Hypothesentests immer korrekt ist, sondern vielmehr, dass das wahrscheinlichste Ergebnis wahr ist.

Beim Hypothesentest auf die Differenz zweier Mittelwerte wird die Teststatistik berechnet und mit dem kritischen Wert verglichen, um die Nullhypothese abzulehnen oder nicht. Im Folgenden erfahren Sie, wie Sie einen Hypothesentest für die Mittelwertdifferenz durchführen.

Denken Sie schließlich daran, dass Hypothesentests in der Statistik auch als Hypothesenkontraste, Hypothesentests oder Signifikanztests bezeichnet werden können.

➤ Siehe: Stichprobenverteilung der Mittelwertdifferenz

Hypothesentestformel für Mittelwertunterschiede

Die Formel, die zum Testen von Hypothesen über die Differenz der Mittelwerte verwendet werden sollte, hängt davon ab, ob die Populationsvarianzen bekannt sind und, falls nicht, davon ausgegangen werden kann, dass sie gleich oder unterschiedlich sind. In diesem Abschnitt werden wir sehen, welche Formel wir je nach Fall verwenden sollten.

Bekannte Variationen

Die Formel zur Berechnung der Hypothesenteststatistik für die Differenz der Mittelwerte bei bekannten Varianzen lautet wie folgt:

$\displaystyle Z=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Gold:

$Z$

ist die Hypothesenteststatistik für die Differenz zweier Mittelwerte mit bekannter Varianz, die einer Standardnormalverteilung folgt.
$\mu_1$

ist der Mittelwert der Bevölkerung 1.
$\mu_2$

ist der Mittelwert der Bevölkerung 2.
$\overline{x_1}$

ist der Mittelwert von Stichprobe 1.
$\overline{x_2}$

ist der Mittelwert von Stichprobe 2.
$\sigma_1$

ist die Standardabweichung der Grundgesamtheit 1.
$\sigma_2$

ist die Standardabweichung der Grundgesamtheit 2.
$n_1$

ist Stichprobengröße 1.
$n_2$

ist Stichprobengröße 2.

Beachten Sie, dass dies der seltenste Fall ist und diese Formel daher nur in bestimmten Fällen verwendet wird.

Unbekannte und gleiche Abweichungen

Die Formel zur Berechnung der Hypothesenteststatistik für die Mittelwertdifferenz, wenn die Populationsvarianzen unbekannt sind, aber als gleich angenommen werden, lautet:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Gold:

$t$

ist die Hypothesenteststatistik für die Mittelwertdifferenz mit unbekannten Varianzen, die einer Student-t-Verteilung mit n ₁ + n ₂ -2 Freiheitsgraden folgt.
$\mu_1$

ist der Mittelwert der Bevölkerung 1.
$\mu_2$

ist der Mittelwert der Bevölkerung 2.
$\overline{x_1}$

ist der Mittelwert von Stichprobe 1.
$\overline{x_2}$

ist der Mittelwert von Stichprobe 2.
$s_p$

ist die kombinierte Standardabweichung.
$n_1$

ist Stichprobengröße 1.
$n_2$

ist Stichprobengröße 2.

Die kombinierte Standardabweichung der beiden Stichproben wird mit der folgenden Formel berechnet:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Unbekannte und unterschiedliche Variationen

Wenn die Populationsvarianzen unbekannt sind und darüber hinaus davon ausgegangen wird, dass sie unterschiedlich sind, lautet die Formel zur Berechnung der Hypothesenteststatistik für die Mittelwertdifferenz wie folgt:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Gold:

$t$

ist die Hypothesenteststatistik für die Mittelwertdifferenz mit unbekannten Varianzen, die der Student-t-Verteilung folgt.
$\mu_1$

ist der Mittelwert der Bevölkerung 1.
$\mu_2$

ist der Mittelwert der Bevölkerung 2.
$\overline{x_1}$

ist der Mittelwert von Stichprobe 1.
$\overline{x_2}$

ist der Mittelwert von Stichprobe 2.
$\sigma_1$

ist die Standardabweichung der Grundgesamtheit 1.
$\sigma_2$

ist die Standardabweichung der Grundgesamtheit 2.
$n_1$

ist Stichprobengröße 1.
$n_2$

ist Stichprobengröße 2.

In diesem Fall werden die Freiheitsgrade der Student-t-Verteilung jedoch anhand der folgenden Formel berechnet:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Siehe: Konfidenzintervallformel für Mittelwertunterschiede

Konkretes Beispiel für die Hypothesenprüfung der Mittelwertdifferenz

Um das Konzept des Hypothesentests auf der Grundlage der Mittelwertdifferenz zu verinnerlichen, sehen wir uns ein konkretes Beispiel für diese Art des Hypothesentests an.

Sie möchten eine statistische Studie zum Gehalt zweier konkurrierender Unternehmen durchführen, genauer gesagt, Sie möchten feststellen, ob das Durchschnittsgehalt der beiden Unternehmen unterschiedlich ist. Hierzu wird eine Stichprobe von 47 Arbeitnehmern des einen Unternehmens und eine weitere Stichprobe von 55 Arbeitnehmern des anderen Unternehmens gezogen. Aus der ersten Stichprobe ergibt sich ein Durchschnittsgehalt von 40.000 US-Dollar und eine Standardabweichung von 12.000 US-Dollar, während aus der zweiten Stichprobe ein Durchschnittsgehalt von 46.000 US-Dollar und eine Standardabweichung von 18.000 US-Dollar ermittelt werden. Führen Sie einen Hypothesentest mit einem Signifikanzniveau von 5 % durch, um festzustellen, ob die Durchschnittsgehälter unterschiedlich sind oder nicht.

In diesem Fall lauten die Nullhypothese und die Alternativhypothese des Hypothesentests für die Differenz der beiden Mittelwerte wie folgt:

$\begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}$

In diesem Fall sind die Bevölkerungsunterschiede nicht bekannt, es kann jedoch davon ausgegangen werden, dass sie gleich sind, da es sich um konkurrierende Unternehmen handelt und die Arbeitsbedingungen auf dem Markt, in dem sie tätig sind, sehr ähnlich sind. Daher lautet die Formel für die Hypothesenteststatistik für die Mittelwertdifferenz, die wir verwenden sollten:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Wir berechnen daher die gepoolte Standardabweichung der beiden Stichproben:

$\begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}$

Wir wenden nun die Hypothesentestformel für die Mittelwertdifferenz an:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\cfrac{(40000-46000)-0}{\displaystyle 15530,61\sqrt{\frac{1}{47}+\frac{1}{55}}}=-1,94$

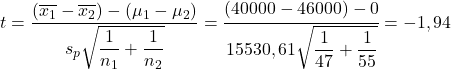
Andererseits suchen wir nach dem kritischen Wert des Hypothesentests für die Mittelwertdifferenz in der Student-t-Tabelle :

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}$

Da der absolute Wert der Teststatistik dann kleiner als der kritische Testwert ist, wird die Nullhypothese akzeptiert und die Alternativhypothese abgelehnt.

$|-1,94|=1,94<1,984 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Was ist ein Hypothesentest für die Mittelwertdifferenz?

Hypothesentestformel für Mittelwertunterschiede

Bekannte Variationen

Unbekannte und gleiche Abweichungen

Unbekannte und unterschiedliche Variationen

Konkretes Beispiel für die Hypothesenprüfung der Mittelwertdifferenz

Über den Autor

Dr. Benjamin Anderson

Einen Kommentar hinzufügen