Variation innerhalb der gruppe oder zwischen gruppen in der anova
Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob die Mittelwerte von drei oder mehr unabhängigen Gruppen gleich sind oder nicht.
Eine einfaktorielle ANOVA verwendet die folgenden Null- und Alternativhypothesen :
- H 0 : Alle Gruppenmittelwerte sind gleich.
- H A : Mindestens ein Gruppendurchschnitt unterscheidet sich von den anderen.
Jedes Mal, wenn Sie eine einfaktorielle ANOVA durchführen, erhalten Sie eine Übersichtstabelle, die wie folgt aussieht:
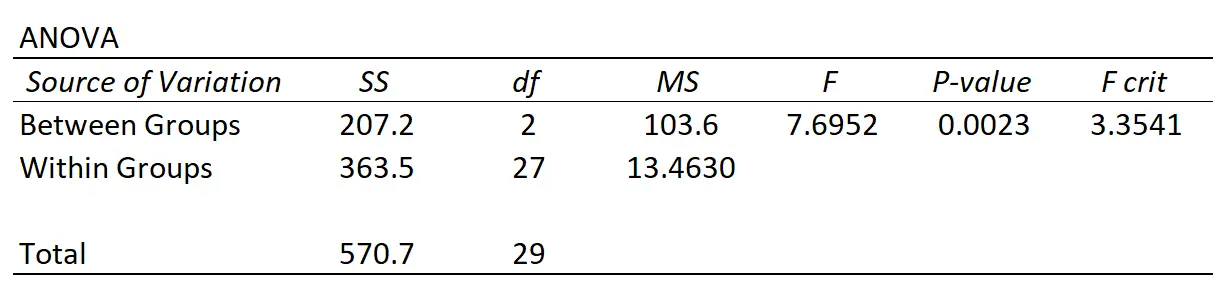
Wir können sehen, dass es zwei verschiedene Variationsquellen gibt, die eine ANOVA misst:
Variation zwischen Gruppen : die Gesamtvariation zwischen dem Durchschnitt jeder Gruppe und dem Gesamtdurchschnitt.
Variation innerhalb der Gruppe : die Gesamtvariation einzelner Werte in jeder Gruppe und ihr Gruppendurchschnitt.
Wenn die Variation zwischen Gruppen im Verhältnis zur Variation innerhalb der Gruppe hoch ist, ist die F-Statistik der ANOVA höher und der entsprechende p-Wert niedriger, wodurch es wahrscheinlicher wird, dass die Nullhypothese abgelehnt wird, nach der die Gruppenmittelwerte sind gleich.
Das folgende Beispiel zeigt, wie die Variation zwischen Gruppen und innerhalb der Gruppe für eine einfaktorielle ANOVA in der Praxis berechnet wird.
Beispiel: Berechnung der Variation innerhalb einer Gruppe und zwischen Gruppen in der ANOVA
Angenommen, wir möchten feststellen, ob drei verschiedene Lernmethoden zu unterschiedlichen durchschnittlichen Prüfungsergebnissen führen. Um dies zu testen, rekrutieren wir 30 Studenten und weisen jedem nach dem Zufallsprinzip 10 zu, eine andere Lernmethode anzuwenden.
Nachfolgend sind die Prüfungsergebnisse der Studierenden jeder Gruppe aufgeführt:
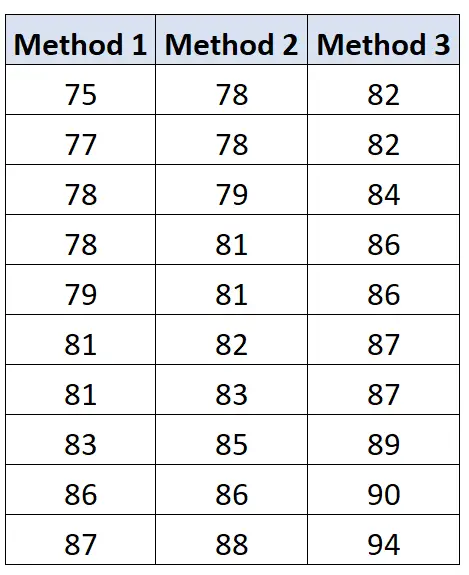
Wir können die folgende Formel verwenden, um die Variation zwischen Gruppen zu berechnen:
Variation zwischen Gruppen = Σn j (X j – X ..) 2
Gold:
- nj : die Stichprobengröße der Gruppe j
- Σ : ein Symbol, das „Summe“ bedeutet
- X j : der Durchschnitt der Gruppe j
- X .. : der Gesamtdurchschnitt
Um diesen Wert zu berechnen, berechnen wir zunächst den Durchschnitt jeder Gruppe und den Gesamtdurchschnitt:
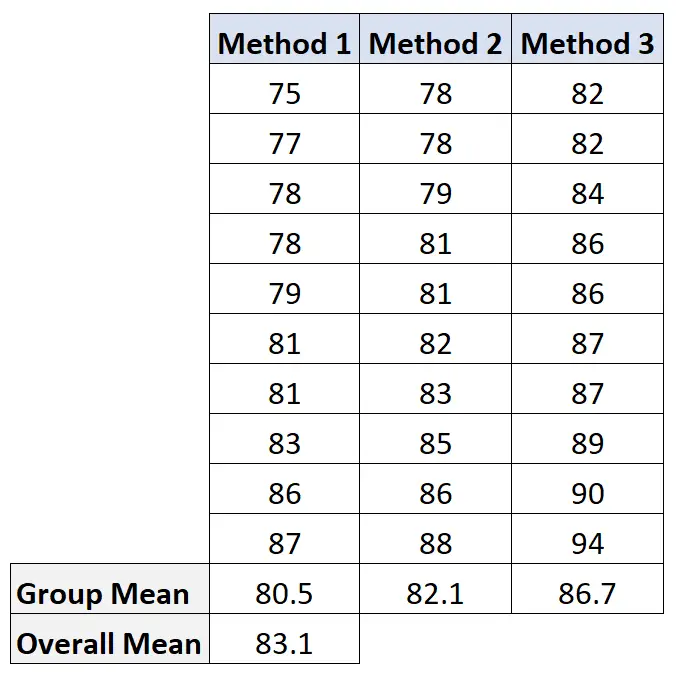
Dann berechnen wir die Variation zwischen den Gruppen wie folgt: 10(80,5-83,1) 2 + 10(82,1-83,1) 2 + 10(86,7-83,1) 2 = 207,2 .
Dann können wir die folgende Formel verwenden, um die Variation innerhalb der Gruppe zu berechnen:
Variation innerhalb der Gruppe : Σ(X ij – X j ) 2
Gold:
- Σ : ein Symbol, das „Summe“ bedeutet
- X ij : die i-te Beobachtung der Gruppe j
- X j : der Durchschnitt der Gruppe j
In unserem Beispiel berechnen wir die Variation innerhalb der Gruppe wie folgt:
Gruppe 1: (75-80,5) 2 + (77-80,5) 2 + (78-80,5) 2 + (78-80,5) 2 + (79-80,5) 2 + (81-80,5) 2 + (81-80,5) 2 + (83-80,5) 2 + (86-80,5) 2 + (87-80,5) 2 = 136,5
Gruppe 2: (78-82,1) 2 + (78-82,1) 2 + (79-82.1) 2 + (81-82.1) 2 + (81-82.1) 2 + (82-82.1) 2 + (83-82.1) 2 + (85-82,1) 2 + (86-82,1) 2 + (88-82,1) 2 = 104,9
Gruppe 3: (82-86,7) 2 + (82-86,7) 2 + (84-86,7) 2 + (86-86,7) 2 + (86-86,7) 2 + (87-86,7) 2 + (87-86,7) 2 + (89-86,7) 2 + (90-86,7) 2 + (94-86,7) 2 = 122,1
Variation innerhalb der Gruppe: 136,5 + 104,9 + 122,1 = 363,5
Wenn wir Statistiksoftware verwenden, um anhand dieses Datensatzes eine einfaktorielle ANOVA durchzuführen, erhalten wir die folgende ANOVA-Tabelle:
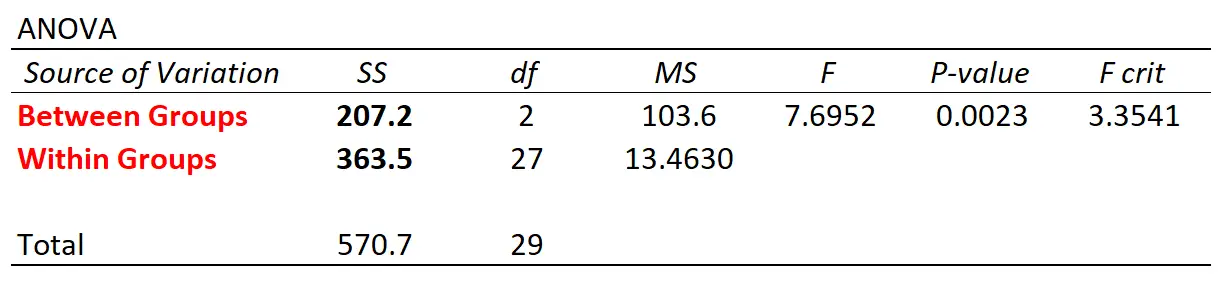
Beachten Sie, dass die Variationswerte zwischen Gruppen und innerhalb der Gruppe mit denen übereinstimmen, die wir manuell berechnet haben.
Die Gesamt-F-Statistik in der Tabelle ist eine Möglichkeit, die Beziehung zwischen der Variation zwischen Gruppen und der Variation innerhalb der Gruppe zu quantifizieren.
Je größer die F-Statistik, desto größer ist die Variation zwischen den Gruppenmitteln im Verhältnis zur Variation innerhalb der Gruppen.
Je größer also die F-Statistik ist, desto offensichtlicher ist es, dass es einen Unterschied zwischen den Gruppenmittelwerten gibt.
In diesem Beispiel können wir sehen, dass der p-Wert, der einer F-Statistik von 7,6952 entspricht, .0023 ist.
Da dieser Wert kleiner als α = 0,05 ist, lehnen wir die Nullhypothese der ANOVA ab und kommen zu dem Schluss, dass die drei Untersuchungstechniken nicht zu derselben Punktzahl in der Prüfung führen.
Zusätzliche Ressourcen
Die folgenden Tutorials bieten zusätzliche Informationen zu ANOVA-Modellen:
Einführung in die einfaktorielle ANOVA
So interpretieren Sie den F-Wert und den P-Wert in der ANOVA
Der vollständige Leitfaden: So melden Sie ANOVA-Ergebnisse
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen