So interpretieren sie asymmetrie in der statistik: mit beispielen

In der Statistik verwenden wir Schiefe , um die Symmetrie einer Verteilung zu beschreiben.

Wir sagen, dass eine Verteilung von Datenwerten schief ist, wenn sie auf der linken Seite der Verteilung einen „Schwanz“ hat:

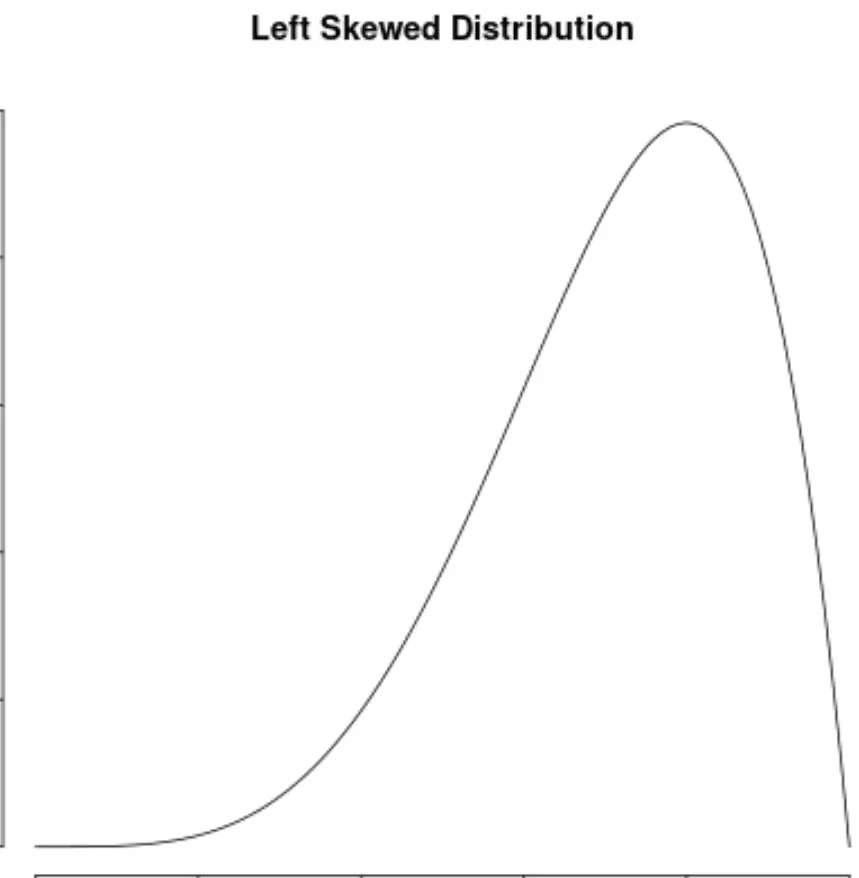
Eine Verteilung heißt rechtsschief , wenn sie auf der rechten Seite der Verteilung einen „Schwanz“ hat:

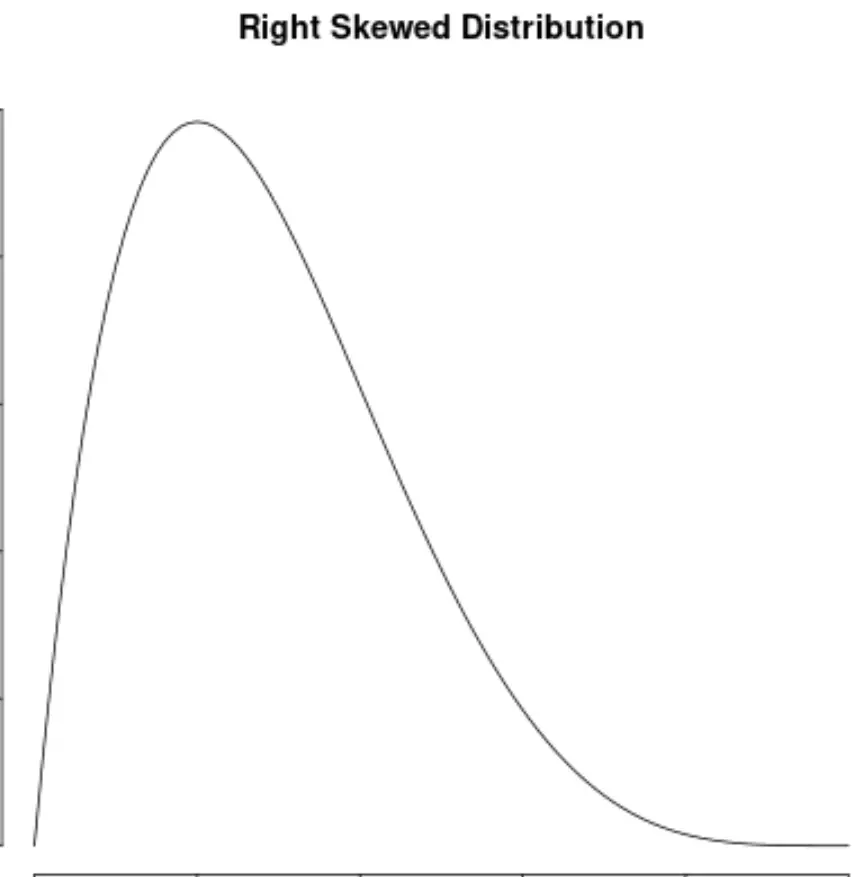
Und wir sagen, dass eine Verteilung keine Asymmetrie hat, wenn sie auf beiden Seiten symmetrisch ist:

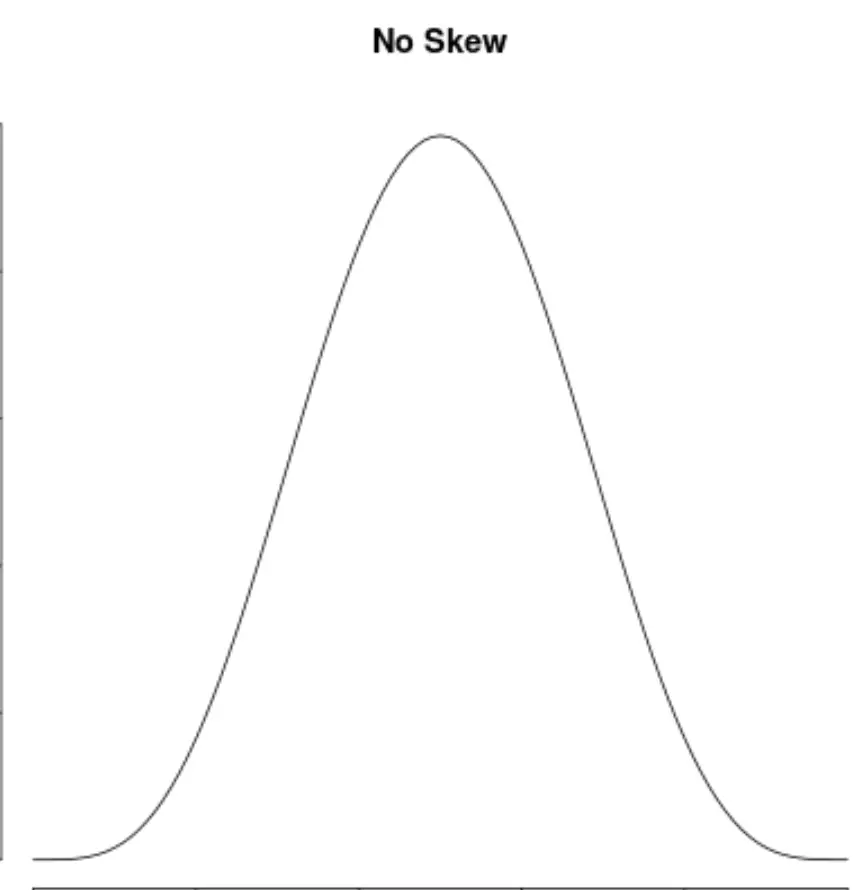
Wie man Asymmetrie interpretiert

Der Wert der Asymmetrie kann von negativ unendlich bis positiv unendlich reichen.

So interpretieren Sie die Asymmetriewerte:

• Ein negativer Wert für die Schiefe zeigt an, dass sich das Ende auf der linken Seite der Verteilung befindet, die sich in Richtung negativerer Werte erstreckt.
• Ein positiver Wert für die Schiefe zeigt an, dass sich das Ende auf der rechten Seite der Verteilung befindet, die sich in Richtung positiverer Werte erstreckt.
• Ein Wert von Null zeigt an, dass die Verteilung keine Asymmetrie aufweist, was bedeutet, dass die Verteilung vollkommen symmetrisch ist.

Die folgenden Beispiele zeigen, wie man Asymmetriewerte in der Praxis interpretiert.

Beispiel 1: linksschiefe Verteilung

Die Altersverteilung der Todesfälle ist in den meisten Bevölkerungsgruppen linksschief. Die meisten Menschen leben zwischen 70 und 80 Jahren, und immer weniger leben darunter.

Wenn wir ein Dichtediagramm erstellen würden, um die Verteilung der Werte für das Sterbealter zu visualisieren, könnte es so aussehen:

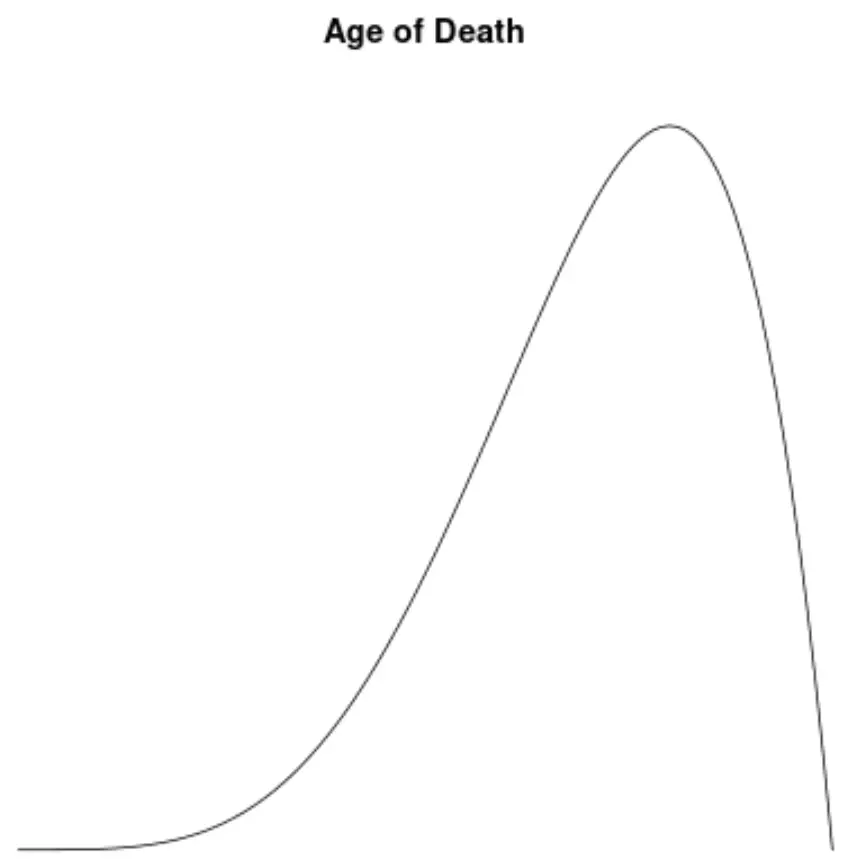
Angenommen, wir berechnen die Schiefe dieser Verteilung und stellen fest, dass sie -1,3225 beträgt.

Da dieser Wert negativ ist, interpretieren wir dies so, dass die Verteilung linksschief ist, was bedeutet, dass sich das Ende zur linken Seite der Verteilung hin erstreckt.

Beispiel 2: rechtsschiefe Verteilung

Die Verteilung des Haushaltseinkommens in den Vereinigten Staaten ist nach rechts verzerrt, wobei die meisten Haushalte zwischen 30.000 und 70.000 US-Dollar pro Jahr verdienen, es gibt aber einen langen rechten Teil der Haushalte, die viel mehr verdienen.

Wenn wir ein Dichtediagramm erstellen, um die Verteilung der Haushaltseinkommenswerte zu visualisieren, könnte es so aussehen:

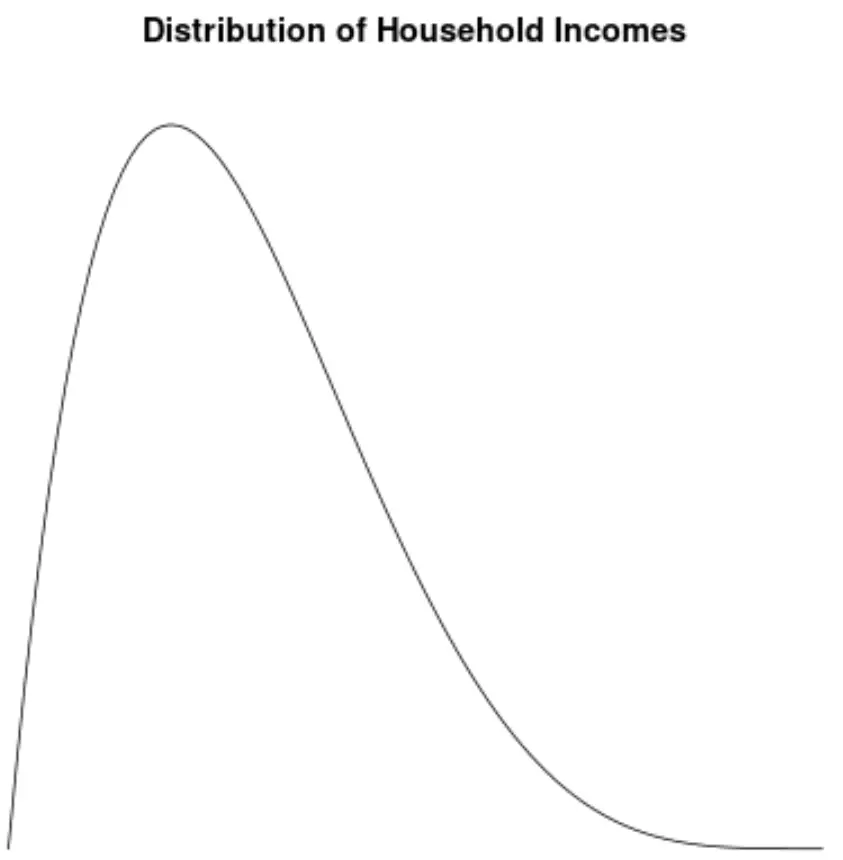
Angenommen, wir berechnen die Schiefe dieser Verteilung und stellen fest, dass sie 2,0043 beträgt.

Da dieser Wert positiv ist, interpretieren wir dies so, dass die Verteilung rechtsschief ist, was bedeutet, dass sich das Ende zur rechten Seite der Verteilung hin erstreckt.

Beispiel 3: Keine Voreingenommenheit

Die Größe der Männchen ist annähernd normal verteilt und weist keine Asymmetrie auf. Beispielsweise beträgt die durchschnittliche Größe eines Mannes in den Vereinigten Staaten etwa 69,1 Zoll. Die Höhenverteilung ist ungefähr symmetrisch, wobei einige kürzer und andere höher sind.

Wenn wir ein Dichtediagramm erstellen würden, um die Verteilung der männlichen Körpergröße in den Vereinigten Staaten zu visualisieren, könnte es so aussehen:

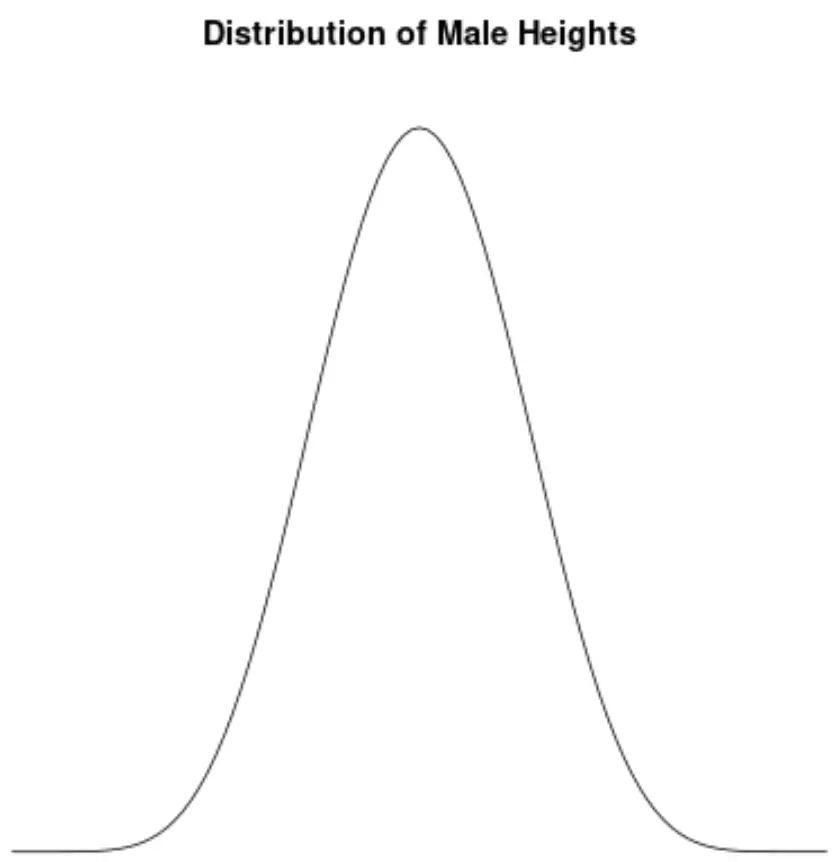
Angenommen, wir berechnen die Schiefe dieser Verteilung und stellen fest, dass sie 0,0013 beträgt.

Da dieser Wert nahe Null liegt, interpretieren wir dies so, dass die Verteilung praktisch keine Schiefe aufweist, was bedeutet, dass die Enden auf beiden Seiten der Verteilung ungefähr gleich sind.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zum Verzerren von Statistiken:

5 Beispiele für positiv verzerrte Verteilungen
5 Beispiele für negativ verzerrte Verteilungen
So berechnen Sie die Schiefe in Excel
So identifizieren Sie Asymmetrie in Boxplots