Wie man cramers v interpretiert (mit beispielen)
Cramers V ist ein Maß für die Stärke der Assoziation zwischen zwei nominalen Variablen.
Es geht von 0 auf 1, wobei:
- 0 bedeutet, dass zwischen den beiden Variablen kein Zusammenhang besteht.
- 1 zeigt eine perfekte Assoziation zwischen den beiden Variablen an.
Es wird wie folgt berechnet:
Cramers V = √ (X 2 /n) / min(c-1, r-1)
Gold:
- X 2 : Die Chi-Quadrat-Statistik
- n: Gesamtstichprobengröße
- r: Anzahl der Zeilen
- c: Anzahl der Spalten
Wie ist Cramers V zu interpretieren?
Die folgende Tabelle zeigt, wie Cramers V entsprechend den Freiheitsgraden zu interpretieren ist:
| Freiheitsgrade | Wenig | DURCHSCHNITT | groß |
|---|---|---|---|
| 1 | 0,10 | 0,30 | 0,50 |
| 2 | 0,07 | 0,21 | 0,35 |
| 3 | 0,06 | 0,17 | 0,29 |
| 4 | 0,05 | 0,15 | 0,25 |
| 5 | 0,04 | 0,13 | 0,22 |
Die folgenden Beispiele zeigen, wie Cramers V in verschiedenen Situationen interpretiert werden kann.
Beispiel 1: Interpretation von Cramers V für ein 2×3-Array
Angenommen, wir möchten wissen, ob ein Zusammenhang zwischen Augenfarbe und Geschlecht besteht. Wir befragen daher 50 Personen und kommen zu folgenden Ergebnissen:
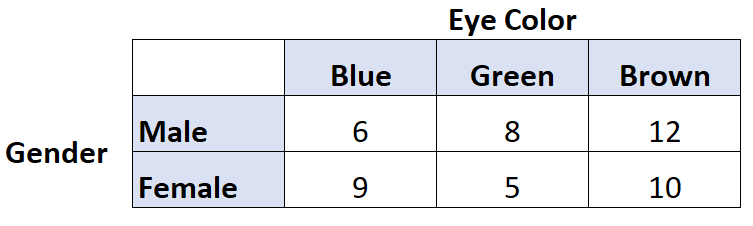
Wir können den folgenden Code in R verwenden, um Cramers V für diese beiden Variablen zu berechnen:
library (rcompanion) #create table data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 ) #view table data [,1] [,2] [,3] [1,] 6 8 12 [2,] 9 5 10 #calculate Cramer's V cramerV(data) Cramer V 0.1671
Es stellt sich heraus, dass Cramers V 0,1671 beträgt.
Die Freiheitsgrade würden wie folgt berechnet:
- df = min(#Zeilen-1, #Spalten-1)
- df = min(1, 2)
- df = 1
Anhand der obigen Tabelle können wir erkennen, dass ein Cramer-V von 0,1671 und Freiheitsgrade = 1 auf einen kleinen (oder „schwachen“) Zusammenhang zwischen Augenfarbe und Geschlecht hinweisen.
Beispiel 2: Interpretation von Cramers V für eine 3×3-Tabelle
Angenommen, wir möchten wissen, ob ein Zusammenhang zwischen der Augenfarbe und der Präferenz für eine politische Partei besteht. Wir befragen daher 50 Personen und kommen zu folgenden Ergebnissen:
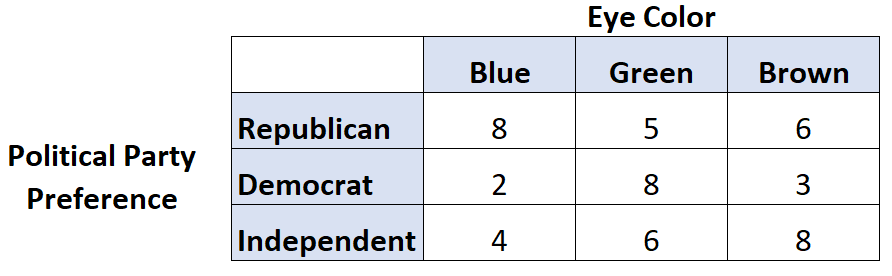
Wir können den folgenden Code in R verwenden, um Cramers V für diese beiden Variablen zu berechnen:
library (rcompanion) #create table data = matrix(c(8, 2, 4, 5, 8, 6, 6, 3, 8), nrow= 3 ) #view table data [,1] [,2] [,3] [1,] 8 5 6 [2,] 2 8 3 [3,] 4 6 8 #calculate Cramer's V cramerV(data) Cramer V 0.246
Es stellt sich heraus, dass Cramers V 0,246 beträgt.
Die Freiheitsgrade würden wie folgt berechnet:
- df = min(#Zeilen-1, #Spalten-1)
- df = min(2, 2)
- df = 2
Anhand der obigen Tabelle können wir erkennen, dass ein Cramer-V von 0,246 und Freiheitsgrade = 2 auf einen mittleren (oder „moderaten“) Zusammenhang zwischen Augenfarbe und Parteipräferenz hinweisen.
Zusätzliche Ressourcen
Die folgenden Tutorials erklären, wie man Cramer’s V in verschiedenen Statistikprogrammen berechnet:
So berechnen Sie Cramers V in Excel
So berechnen Sie Cramers V in R
So berechnen Sie Cramers V in Python