So interpretieren sie log-likelihood-werte (mit beispielen)

Der Log-Likelihood-Wert eines Regressionsmodells ist eine Möglichkeit, die Anpassungsgüte eines Modells zu messen. Je höher der Log-Likelihood-Wert, desto besser passt das Modell zu einem Datensatz.

Der Wert der Log-Likelihood für ein bestimmtes Modell kann von negativ unendlich bis positiv unendlich reichen. Der tatsächliche Log-Likelihood-Wert für ein bestimmtes Modell ist im Allgemeinen bedeutungslos, aber für den Vergleich von zwei oder mehr Modellen nützlich .

In der Praxis passen wir häufig mehrere Regressionsmodelle an einen Datensatz an und wählen das Modell mit dem höchsten Log-Likelihood-Wert als das Modell aus, das am besten zu den Daten passt.

Das folgende Beispiel zeigt, wie Log-Likelihood-Werte für verschiedene Regressionsmodelle in der Praxis interpretiert werden.

Beispiel: Interpretieren von Log-Likelihood-Werten

Nehmen wir an, wir haben den folgenden Datensatz, der die Anzahl der Schlafzimmer, die Anzahl der Badezimmer und die Verkaufspreise von 20 verschiedenen Häusern in einer bestimmten Nachbarschaft zeigt:

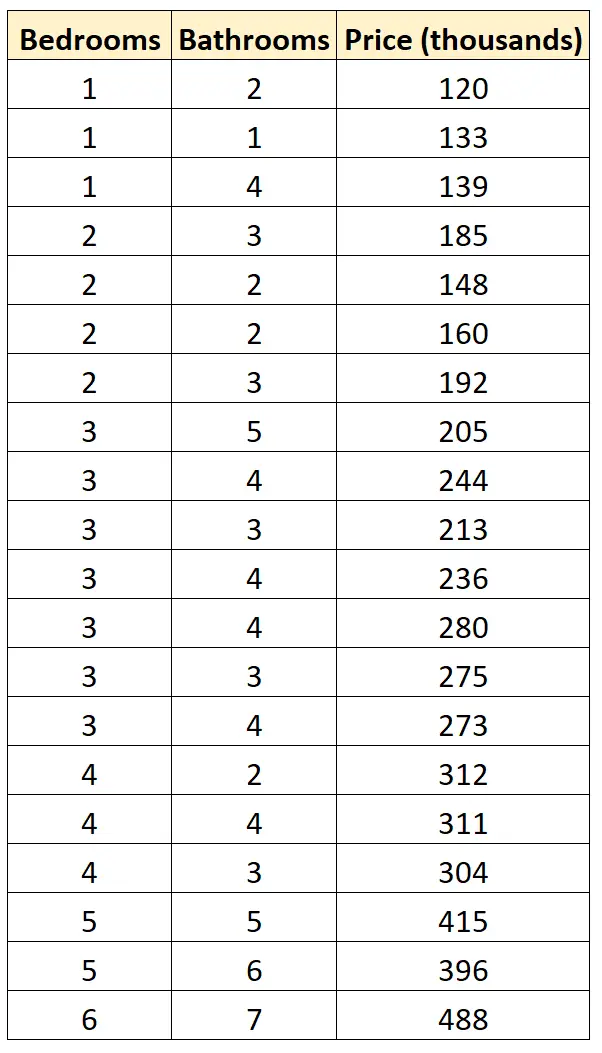
Angenommen, wir möchten die folgenden zwei Regressionsmodelle anpassen und bestimmen, welches die beste Anpassung an die Daten bietet:

Modell 1 : Preis = β ₀ + β ₁ (Anzahl der Zimmer)

Modell 2 : Preis = β ₀ + β ₁ (Anzahl Badezimmer)

Der folgende Code zeigt, wie jedes Regressionsmodell angepasst und der Log-Likelihood-Wert jedes Modells in R berechnet wird:

 #define data
df <- data. frame (beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
                        3, 3, 3, 3, 4, 4, 4, 5, 5, 6),
                 baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3,
                         4, 4, 3, 4, 2, 4, 3, 5, 6, 7),
                 price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213,
                         236, 280, 275, 273, 312, 311, 304, 415, 396, 488))

#fitmodels
model1 <- lm(price~beds, data=df)
model2 <- lm(price~baths, data=df)

#calculate log-likelihood value of each model
logLik(model1)

'log Lik.' -91.04219 (df=3)

logLik(model2)

'log Lik.' -111.7511 (df=3)

Das erste Modell hat einen höheren Log-Likelihood-Wert ( -91,04 ) als das zweite Modell ( -111,75 ), was bedeutet, dass das erste Modell eine bessere Anpassung an die Daten bietet.

Vorsichtsmaßnahmen für die Verwendung von Log-Likelihood-Werten

Bei der Berechnung von Log-Likelihood-Werten ist zu beachten, dass das Hinzufügen zusätzlicher Prädiktorvariablen zu einem Modell fast immer zu einer Erhöhung des Log-Likelihood-Werts führt, selbst wenn die zusätzlichen Prädiktorvariablen statistisch nicht signifikant sind.

Das bedeutet, dass Sie Log-Likelihood-Werte zwischen zwei Regressionsmodellen nur dann vergleichen sollten, wenn jedes Modell über die gleiche Anzahl an Prädiktorvariablen verfügt.

Um Modelle mit einer unterschiedlichen Anzahl von Prädiktorvariablen zu vergleichen, können Sie einen Likelihood-Ratio-Test durchführen, um die Anpassungsgüte zweier verschachtelter Regressionsmodelle zu vergleichen.

Zusätzliche Ressourcen

So verwenden Sie die Funktion lm(), um lineare Modelle in R anzupassen
So führen Sie einen Likelihood-Ratio-Test in R durch