Interquartilbereich (oder interquartilbereich)
In diesem Artikel wird erläutert, was der Interquartilbereich, auch Interquartilbereich genannt, ist. Außerdem können Sie anhand eines konkreten Beispiels sehen, wie der Interquartilbereich berechnet wird. Sie erfahren, wozu der Interquartilbereich dient und welchen Unterschied er zum Intervall macht. Darüber hinaus können Sie den Interquartilbereich jedes Datensatzes mit einem Online-Rechner berechnen.
Was ist der Interquartilbereich (oder Interquartilbereich)?
Der Interquartilabstand, auch Interquartilabstand genannt, ist ein Maß für die statistische Streuung, das den Unterschied zwischen dem dritten und dem ersten Quartil angibt. Um den Interquartilbereich eines statistischen Datensatzes zu berechnen, müssen Sie daher zunächst das dritte und erste Quartil ermitteln und diese dann subtrahieren.
Kurz gesagt wird der Interquartilbereich durch das Akronym IQR ausgedrückt.
Eine der vorteilhaftesten Eigenschaften des Interquartilbereichs besteht darin, dass es sich um eine robuste Statistik handelt, das heißt, sie weist eine hohe Robustheit gegenüber Ausreißern auf. Da Extremwerte bei der Berechnung des Interquartilbereichs nicht berücksichtigt werden, ändert sich sein Wert kaum, wenn neue Ausreißer auftreten.
Offensichtlich gibt es neben dem Interquartilbereich noch andere Streuungsmaße. Die bekanntesten Maßstäbe sind die Spanne, die Varianz, die Standardabweichung (oder Standardabweichung), die mittlere Abweichung und der Variationskoeffizient.
So berechnen Sie den Interquartil- (oder Interquartil-)Bereich
Um in der Statistik den Interquartilbereich (oder Interquartilbereich) eines Datensatzes zu berechnen, müssen Sie zunächst das erste und dritte Quartil des Datensatzes ermitteln und dann die Subtraktion des dritten Quartils minus dem ersten Quartil berechnen.
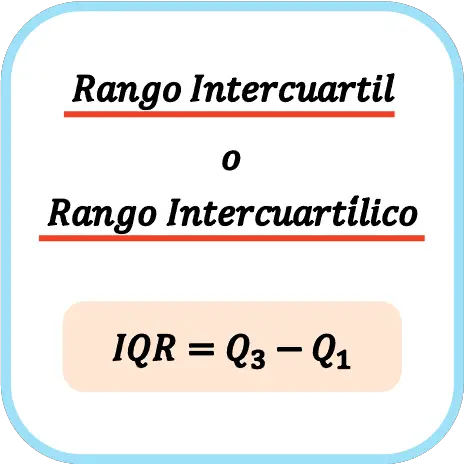
Daher lautet die Formel zur Berechnung des Interquartilbereichs oder Interquartilbereichs:
👉 Mit dem Rechner unten können Sie den Interquartilbereich für jeden Datensatz berechnen.
Daher ist es wichtig, dass Sie wissen, wie die Quartile einer statistischen Stichprobe berechnet werden. Aus diesem Grund empfehle ich Ihnen, bevor Sie fortfahren, den folgenden Artikel zu lesen und dann mit der Erklärung fortzufahren.
Beispiel für einen Interquartil- (oder Interquartil-)Bereich
Anhand der Definition und Formel für den Interquartilbereich (oder Interquartilbereich) finden Sie unten eine gelöste Übung, damit Sie genau sehen können, wie diese Art von Streuungsmaß berechnet wird.
- Wir wollen statistisch analysieren, ob es sinnvoll ist, in ein Unternehmen zu investieren. Dazu haben wir Daten zum Aktienkurs dieses Unternehmens in den letzten 15 Monaten gesammelt. In der folgenden Tabelle sehen Sie die beobachteten Daten, sortiert vom niedrigsten zum höchsten Wert. Berechnen Sie den Interquartilbereich für diesen Datensatz.

Wie wir im vorherigen Abschnitt gesehen haben, müssen wir zunächst das erste und dritte Quartil berechnen, um den Interquartilbereich (oder Interquartilbereich) der Stichprobe zu erhalten.
Das erste Quartil ist der Median der ersten Hälfte der Werte, was 8,95 €/Aktie entspricht.
![]()
Das dritte Quartil hingegen ist der Zwischenwert der zweiten Hälfte der Werte, es liegt also bei 9,83 €/Aktie.
![]()
Um den Interquartilbereich zu ermitteln, wenden Sie einfach die Formel an und subtrahieren Sie das dritte Quartil minus das erste Quartil.
![]()
Interquartil- (oder Interquartil-)Bereichsrechner
Geben Sie einen statistischen Datensatz in den folgenden Rechner ein, um seinen Interquartilsabstand oder Interquartilsabstand zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.
Unterschied zwischen Interquartilbereich und Bereich
In der Statistik sind die Differenz zwischen dem Interquartilbereich (oder Interquartilbereich) und dem Intervall die Werte, die zur Durchführung der Berechnung herangezogen werden. Der Interquartilbereich ist die Differenz zwischen dem dritten und dem ersten Quartil, während der Bereich die Differenz zwischen den Extremwerten der Stichprobe ist.
Somit misst der Interquartilbereich die Streuung einer Stichprobe anhand der zentralen Daten, während das Intervall die Streuung der Stichprobe anhand der Extremdaten quantifiziert.
Daher wird der statistische Bereich viel stärker von Ausreißern beeinflusst, da sie normalerweise das Minimum oder Maximum des Datensatzes darstellen. Einer der Vorteile des Interquartilbereichs gegenüber dem Intervall besteht daher darin, dass er eine größere Robustheit aufweist.
Wofür wird der Interquartilbereich (oder Interquartilbereich) verwendet?
In erster Linie wird der Interquartilabstand (oder auch Interquartilabstand) verwendet, um die Verteilung eines Datensatzes zu messen . Obwohl die Analyse der Streuung einer Stichprobe die Berechnung weiterer statistischer Maße erfordert, liefert der Interquartilbereich eine Vorstellung davon, wie gestreut die Stichprobe ist, zumindest in Bezug auf die zentralen Werte.
Die Interpretation des Interquartilbereichs ist daher relativ einfach. Je höher der Wert des Interquartilbereichs ist, desto stärker sind die mittleren Daten in der Stichprobe verteilt, und je kleiner der Interquartilbereich, desto näher liegen die mittleren Daten beieinander.
Darüber hinaus eignet sich der Interquartilbereich auch zur Erstellung eines Box-and-Whisker-Diagramms, einem häufig verwendeten Diagramm zur Analyse des Aktienkursverhaltens an der Börse.