So berechnen sie den interquartilbereich (iqr) in excel

In diesem Tutorial wird erläutert, wie Sie den Interquartilbereich eines Datensatzes in Excel berechnen.

Was ist der Interquartilbereich?

Der Interquartilbereich , oft IQR genannt, ist eine Möglichkeit , die Verteilung der mittleren 50 % eines Datensatzes zu messen. Sie wird als Differenz zwischen dem ersten Quartil* (Q1) und dem dritten Quartil (Q3) eines Datensatzes berechnet.

*Quartile sind einfach Werte, die einen Datensatz in vier gleiche Teile teilen.

Angenommen, wir haben den folgenden Datensatz:

[58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98]

Das dritte Quartil beträgt 91 und das erste Quartil 75,5 . Der Interquartilbereich (IQR) für diesen Datensatz beträgt also 91 – 75,5 = 15 . Dies verrät uns die Verteilung der mittleren 50 % der Werte in diesem Datensatz.

So berechnen Sie den Interquartilbereich in Excel

Microsoft Excel verfügt nicht über eine integrierte Funktion zur Berechnung des IQR eines Datensatzes, aber wir können sie leicht mit der Funktion QUARTILE() finden, die die folgenden Argumente akzeptiert:

QUARTIL(Array, Viertel)

• Array: das Datenarray, an dem Sie interessiert sind.
• Quart: das Quartil, das Sie berechnen möchten.

Beispiel: Suche nach IQR in Excel

Angenommen, wir möchten den IQR für den folgenden Datensatz ermitteln:

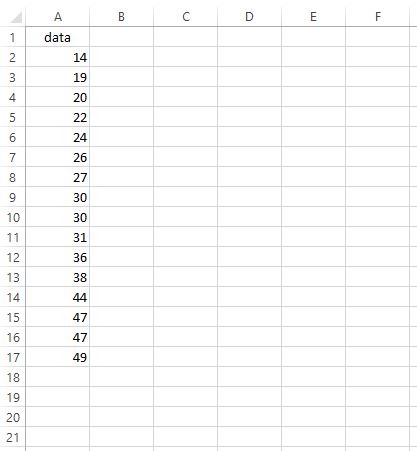
Um den IQR zu ermitteln, können wir die folgenden Schritte ausführen:

Schritt 1: Suchen Sie nach Q1 .

Um das erste Quartil zu finden, geben wir einfach =QUARTILE(A2:A17, 1) in eine beliebige Zelle ein:

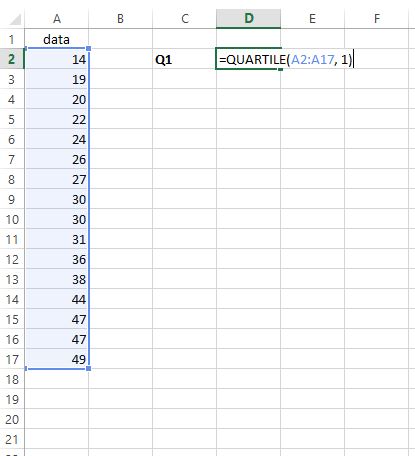
Schritt 2: Suchen Sie nach Q3 .

Um das dritte Quartil zu finden, geben wir =QUARTILE(A2:A17, 3) in eine beliebige Zelle ein:

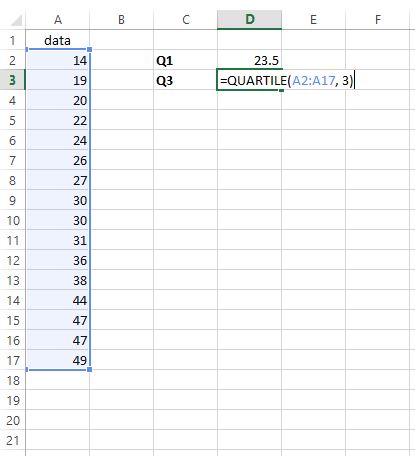
Schritt 3: IQR finden .

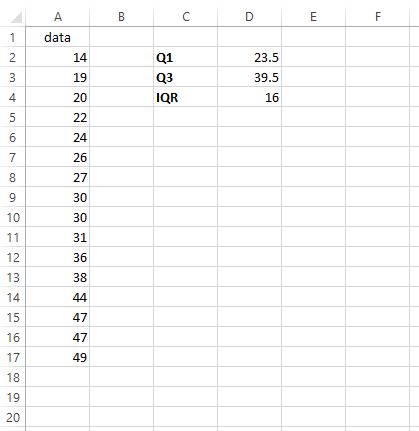
Um den Interquartilbereich (IQR) zu ermitteln, subtrahieren wir einfach Q1 von Q3:

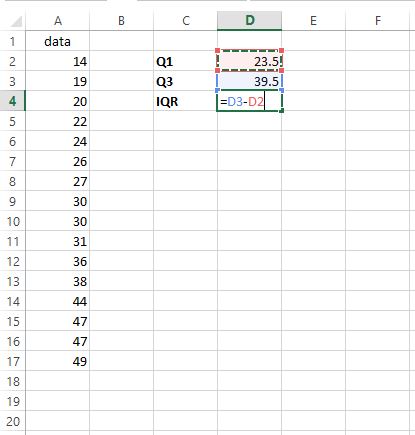
Der IQR beträgt 39,5 – 23,5 = 16 . Dies sagt uns, wie verteilt die mittleren 50 % der Werte in diesem bestimmten Datensatz sind.

Ein kürzerer Ansatz

Beachten Sie, dass wir den Interquartilbereich des Datensatzes im vorherigen Beispiel auch mithilfe einer Formel hätten ermitteln können:

=QUARTIL(A2:A17, 3) – QUARTIL(A2:A17, 1)

Dies würde ebenfalls den Wert 16 ergeben.

Abschluss

Der Interquartilbereich ist nur eine Möglichkeit, die „Spreizung“ eines Datensatzes zu messen. Andere Methoden zur Messung der Streuung sind Spanne, Standardabweichung und Varianz.

Der Vorteil der Verwendung von IQR zur Messung der Ausbreitung besteht darin, dass es robust gegenüber Ausreißern ist . Da es uns nur die Verteilung der mittleren 50 % des Datensatzes mitteilt, wird es nicht durch ungewöhnlich kleine oder ungewöhnlich große Ausreißer beeinflusst.

Dies macht es zu einer bevorzugten Methode zur Messung der Streuung im Vergleich zu einem metrischen Bereich, der uns einfach die Differenz zwischen dem größten und dem kleinsten Wert in einem Datensatz angibt.

Verwandte Themen: So berechnen Sie den Mittelwert in Excel