Inverse normalverteilung: definition und beispiel
Der Begriff „inverse Normalverteilung“ bezieht sich auf die Methode, eine bekannte Wahrscheinlichkeit zu verwenden, um den entsprechenden z-kritischen Wert in einer Normalverteilung zu finden.
Dies sollte nicht mit der inversen Gaußschen Verteilung verwechselt werden, bei der es sich um eine kontinuierliche Wahrscheinlichkeitsverteilung handelt.
Dieses Tutorial bietet mehrere Beispiele für die Verwendung der inversen Normalverteilung in verschiedenen Statistiksoftware.
Für die umgekehrte Normalverteilung haben wir den Rechner TI-83 oder TI-84
Am wahrscheinlichsten stoßen Sie auf den Begriff „inverse Normalverteilung“ auf einem TI-83- oder TI-84-Rechner, der die folgende Funktion verwendet, um den kritischen Z-Wert zu ermitteln, der einer bestimmten Wahrscheinlichkeit entspricht:
invNorm(Wahrscheinlichkeit, μ, σ)
Gold:
- Wahrscheinlichkeit: das Signifikanzniveau
- μ: Bevölkerungsdurchschnitt
- σ: Populationsstandardabweichung
Sie können auf diese Funktion auf einem TI-84-Rechner zugreifen, indem Sie 2nd und dann vars drücken. Dadurch gelangen Sie zu einem DISTR- Bildschirm, auf dem Sie dann invNorm() verwenden können:

Mit dieser Funktion können wir beispielsweise den z-kritischen Wert ermitteln, der einem Wahrscheinlichkeitswert von 0,05 entspricht:
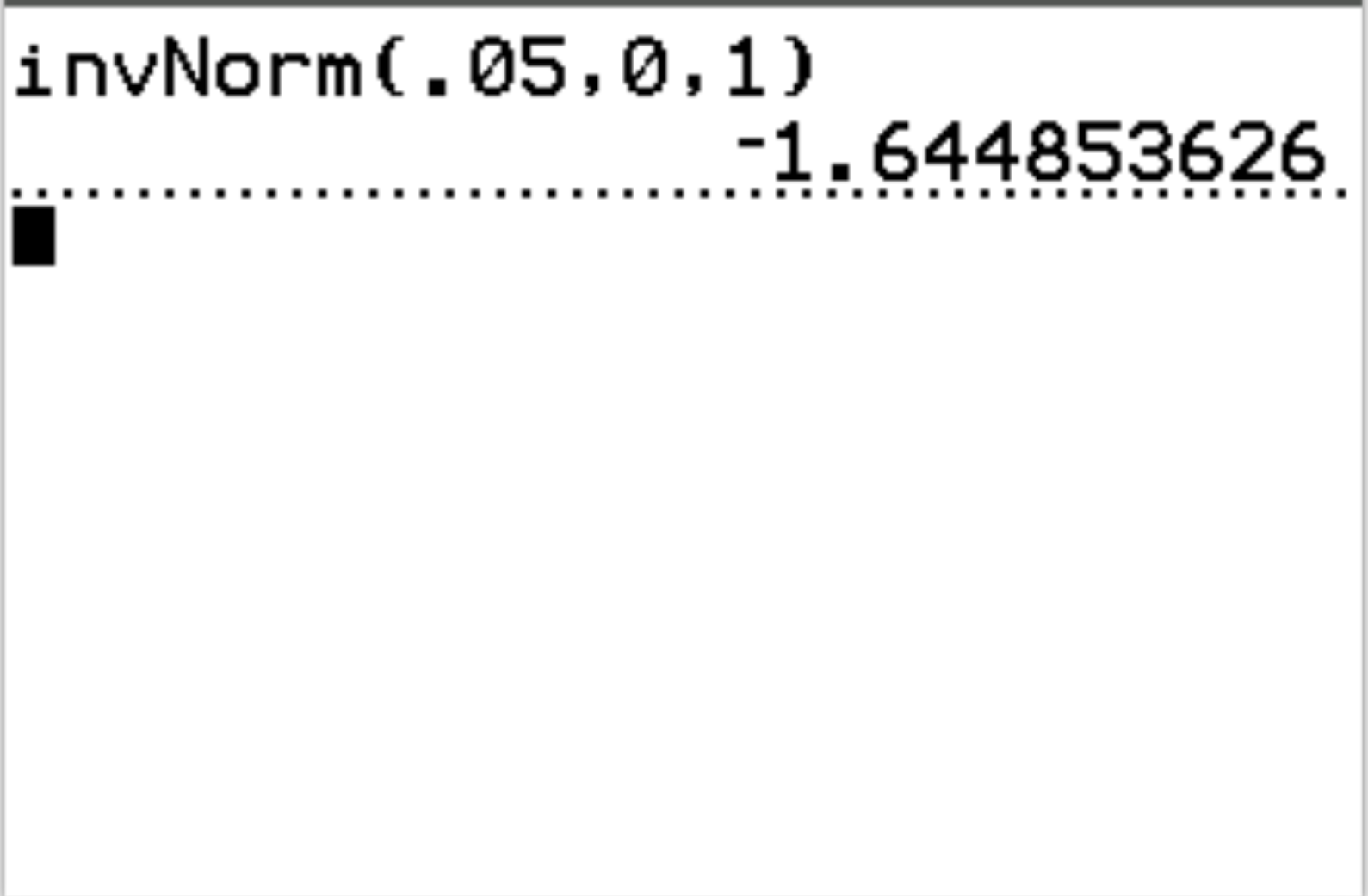
Der kritische Z-Wert, der einem Wahrscheinlichkeitswert von 0,05 entspricht, ist -1,64485 .
Verwandte Themen: So verwenden Sie invNorm auf einem TI-84-Rechner (mit Beispielen)
Inverse Normalverteilung in Excel
Um den z-kritischen Wert zu finden, der einem bestimmten Wahrscheinlichkeitswert in Excel zugeordnet ist, können wir die Funktion INVNORM() verwenden, die die folgende Syntax verwendet:
INVNORM(p, Mittelwert, SD)
Gold:
- p: das Signifikanzniveau
- Durchschnitt: Bevölkerungsdurchschnitt
- sd: Populationsstandardabweichung
Mit dieser Funktion können wir beispielsweise den z-kritischen Wert ermitteln, der einem Wahrscheinlichkeitswert von 0,05 entspricht:
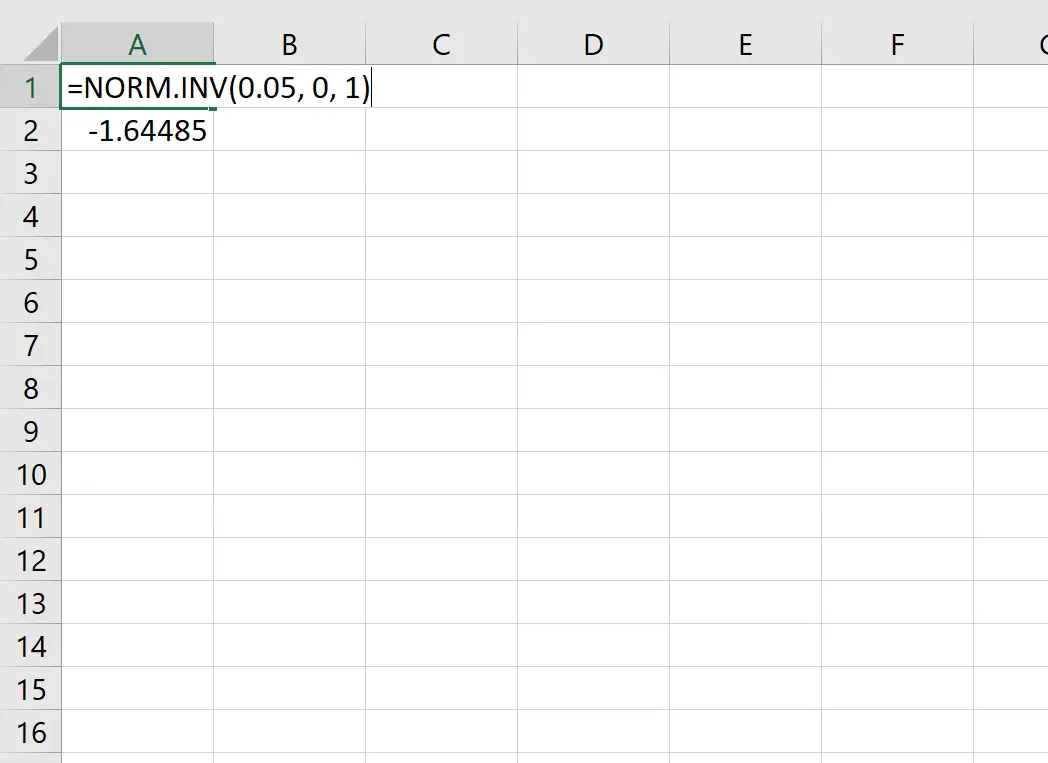
Der kritische Z-Wert, der einem Wahrscheinlichkeitswert von 0,05 entspricht, ist -1,64485 .
Inverse Normalverteilung in R
Um den z-kritischen Wert zu finden, der einem bestimmten Wahrscheinlichkeitswert in R zugeordnet ist, können wir die Funktion qnorm() verwenden, die die folgende Syntax verwendet:
qnorm (p, Mittelwert, SD)
Gold:
- p: das Signifikanzniveau
- Durchschnitt: Bevölkerungsdurchschnitt
- sd: Populationsstandardabweichung
Mit dieser Funktion können wir beispielsweise den z-kritischen Wert ermitteln, der einem Wahrscheinlichkeitswert von 0,05 entspricht:
qnorm (p= .05 , mean= 0 , sd= 1 ) [1] -1.644854
Auch hier beträgt der kritische Z-Wert, der einem Wahrscheinlichkeitswert von 0,05 entspricht, -1,64485 .