So verwenden sie invnorm auf einem ti-84-rechner (mit beispielen)

Sie können die Funktion invNorm() auf einem TI-84-Rechner verwenden, um z-kritische Werte zu finden, die mit der Normalverteilung verknüpft sind.

Diese Funktion verwendet die folgende Syntax:

invNorm(Wahrscheinlichkeit, μ, σ)

Gold:

• Wahrscheinlichkeit: das Signifikanzniveau
• μ: Bevölkerungsdurchschnitt
• σ: Populationsstandardabweichung

Sie können auf diese Funktion auf einem TI-84-Rechner zugreifen, indem Sie 2nd und dann VARS drücken. Dadurch gelangen Sie zu einem DISTR- Bildschirm, auf dem Sie dann invNorm() verwenden können:

Die folgenden Beispiele zeigen, wie Sie diese Funktion in der Praxis nutzen können.

Beispiel 1: Kritischer Z-Wert für einseitige Tests

Angenommen, ein Forscher führt einen linkshändigen Hypothesentest mit α = 0,05 durch. Was ist der z-kritische Wert, der diesem Alpha-Level entspricht?

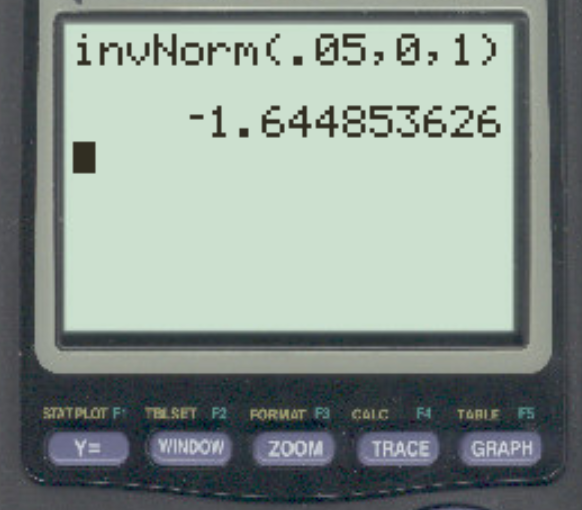
Die Antwort ist z = -1,64485 .

Angenommen, ein Forscher führt einen direkten Hypothesentest mit α = 0,05 durch. Was ist der z-kritische Wert, der diesem Alpha-Level entspricht?

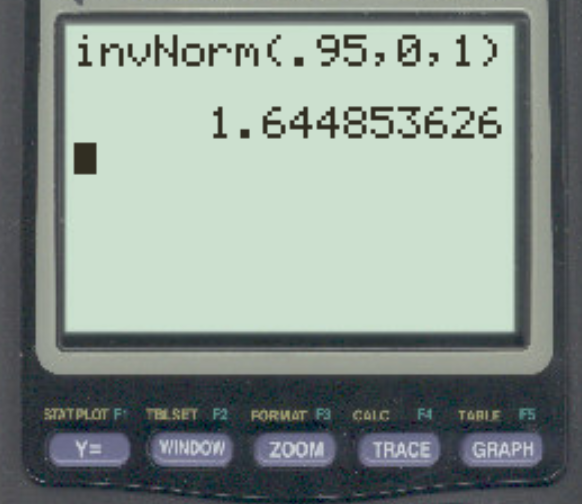
Die Antwort ist z = 1,64485 .

Beispiel 2: Kritischer Z-Wert für zweiseitige Tests

Angenommen, ein Forscher führt einen zweiseitigen Hypothesentest mit α = 0,05 durch. Was ist der z-kritische Wert, der diesem Alpha-Level entspricht?

Um diesen kritischen Wert zu ermitteln, können wir die Formel 1 – α/2 verwenden. In diesem Fall verwenden wir 1 – 0,05/2 = 0,975 für die Wahrscheinlichkeit:

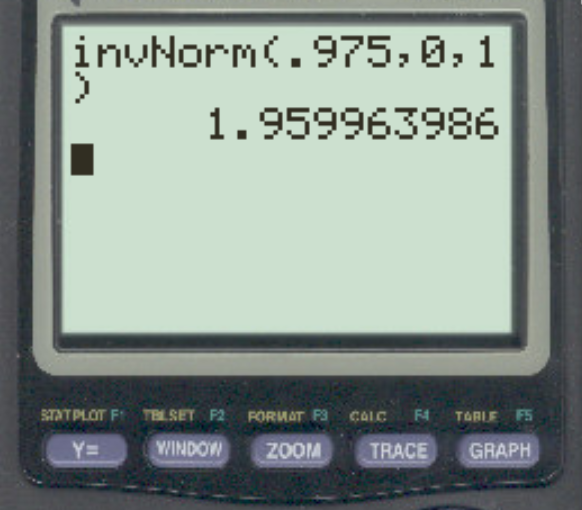
Die Antwort ist z = 1,96 .

Beispiel 3: Kritischer Z-Wert für Cutoff-Scores

Angenommen, die Ergebnisse einer bestimmten Prüfung sind normalverteilt mit einem Mittelwert von 70 und einer Standardabweichung von 8. Welche Punktzahl unterscheidet die besten 10 % vom Rest?

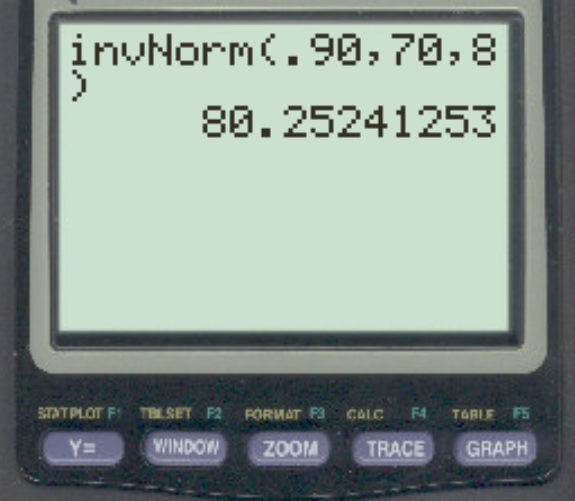
Die Antwort ist 80,25 .

Angenommen, die Körpergröße von Männern in einer bestimmten Stadt ist normalverteilt mit einem Mittelwert von 68 Zoll und einer Standardabweichung von 4 Zoll. Wie hoch sind die unteren 25 % vom Rest?

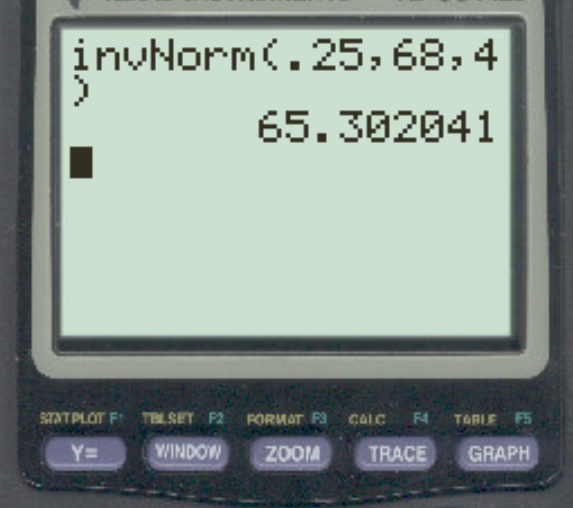
Die Antwort ist 65,3 Zoll.

Zusätzliche Ressourcen

So berechnen Sie Binomialwahrscheinlichkeiten mit einem TI-84-Rechner
So berechnen Sie Poisson-Wahrscheinlichkeiten mit einem TI-84-Rechner
So berechnen Sie geometrische Wahrscheinlichkeiten mit einem TI-84-Rechner