K-means-clustering in python: schritt-für-schritt-beispiel

Einer der gebräuchlichsten Clustering-Algorithmen beim maschinellen Lernen ist das sogenannte K-Means-Clustering .

K-Means-Clustering ist eine Technik, bei der wir jede Beobachtung aus einem Datensatz in einem von K Clustern platzieren.

Das Endziel besteht darin, K- Cluster zu haben, in denen die Beobachtungen innerhalb jedes Clusters einander ziemlich ähnlich sind, während sich die Beobachtungen in verschiedenen Clustern deutlich voneinander unterscheiden.

In der Praxis verwenden wir die folgenden Schritte, um K-Means-Clustering durchzuführen:

1. Wählen Sie einen Wert für K.

• Zunächst müssen wir entscheiden, wie viele Cluster wir in den Daten identifizieren möchten. Oft müssen wir einfach mehrere verschiedene Werte für K testen und die Ergebnisse analysieren, um zu sehen, welche Anzahl von Clustern für ein bestimmtes Problem am sinnvollsten erscheint.

2. Ordnen Sie jede Beobachtung zufällig einem Anfangscluster von 1 bis K zu.

3. Führen Sie das folgende Verfahren aus, bis sich die Clusterzuweisungen nicht mehr ändern.

• Berechnen Sie für jeden der K- Cluster den Schwerpunkt des Clusters. Dies ist einfach der Vektor der p- Mittelwert-Merkmale für die Beobachtungen des k-ten Clusters.
• Ordnen Sie jede Beobachtung dem Cluster mit dem nächstgelegenen Schwerpunkt zu. Hier wird der Abstand mithilfe des euklidischen Abstands definiert.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie K-Means-Clustering in Python mithilfe der KMeans- Funktion aus dem Sklearn- Modul durchführen.

Schritt 1: Importieren Sie die erforderlichen Module

Zuerst importieren wir alle Module, die wir zum Durchführen von K-Means-Clustering benötigen:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

Schritt 2: Erstellen Sie den DataFrame

Als Nächstes erstellen wir einen DataFrame, der die folgenden drei Variablen für 20 verschiedene Basketballspieler enthält:

• Punkte
• helfen
• springt

Der folgende Code zeigt, wie dieser Pandas-DataFrame erstellt wird:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#view first five rows of DataFrame
print ( df.head ())

   points assists rebounds
0 18.0 3.0 15
1 NaN 3.0 14
2 19.0 4.0 14
3 14.0 5.0 10
4 14.0 4.0 8

Wir werden K-Means-Clustering verwenden, um ähnliche Akteure basierend auf diesen drei Metriken zu gruppieren.

Schritt 3: Bereinigen und bereiten Sie den DataFrame vor

Dann führen wir die folgenden Schritte durch:

• Verwenden Sie dropna() , um Zeilen mit NaN-Werten in einer beliebigen Spalte zu löschen
• Verwenden Sie StandardScaler() , um jede Variable so zu skalieren, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 hat.

Der folgende Code zeigt, wie das geht:

 #drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

#view first five rows of scaled DataFrame
print (scaled_df[:5])

[[-0.86660275 -1.22683918 1.72722524]
 [-0.72081911 -0.96077767 1.45687694]
 [-1.44973731 -0.69471616 0.37548375]
 [-1.44973731 -0.96077767 -0.16521285]
 [-1.88708823 -0.16259314 1.45687694]]

Hinweis : Wir verwenden die Skalierung, damit jede Variable bei der Anpassung des k-means-Algorithmus die gleiche Bedeutung hat. Andernfalls hätten die Variablen mit den größten Spannweiten einen zu großen Einfluss.

Schritt 4: Finden Sie die optimale Anzahl an Clustern

Um K-Means-Clustering in Python durchzuführen, können wir die KMeans- Funktion aus dem Sklearn- Modul verwenden.

Diese Funktion verwendet die folgende grundlegende Syntax:

KMeans(init=’random‘, n_clusters=8, n_init=10, random_state=None)

Gold:

• init : Steuert die Initialisierungstechnik.
• n_clusters : die Anzahl der Cluster, in denen die Beobachtungen platziert werden sollen.
• n_init : Die Anzahl der durchzuführenden Initialisierungen. Standardmäßig wird der k-means-Algorithmus zehnmal ausgeführt und derjenige mit dem niedrigsten SSE zurückgegeben.
• random_state : Ein ganzzahliger Wert, den Sie auswählen können, um die Ergebnisse des Algorithmus reproduzierbar zu machen.

Das wichtigste Argument dieser Funktion ist n_clusters, das angibt, in wie vielen Clustern Beobachtungen platziert werden sollen.

Da wir jedoch nicht im Voraus wissen, wie viele Cluster optimal sind, müssen wir ein Diagramm erstellen, das die Anzahl der Cluster sowie die SSE (Summe der quadratischen Fehler) des Modells anzeigt.

Wenn wir diese Art von Diagramm erstellen, suchen wir normalerweise nach einem „Knie“, an dem die Summe der Quadrate beginnt, sich zu „biegen“ oder einzuebnen. Dies ist im Allgemeinen die optimale Anzahl von Clustern.

Der folgende Code zeigt, wie man diese Art von Diagramm erstellt, das die Anzahl der Cluster auf der x-Achse und den SSE auf der y-Achse anzeigt:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

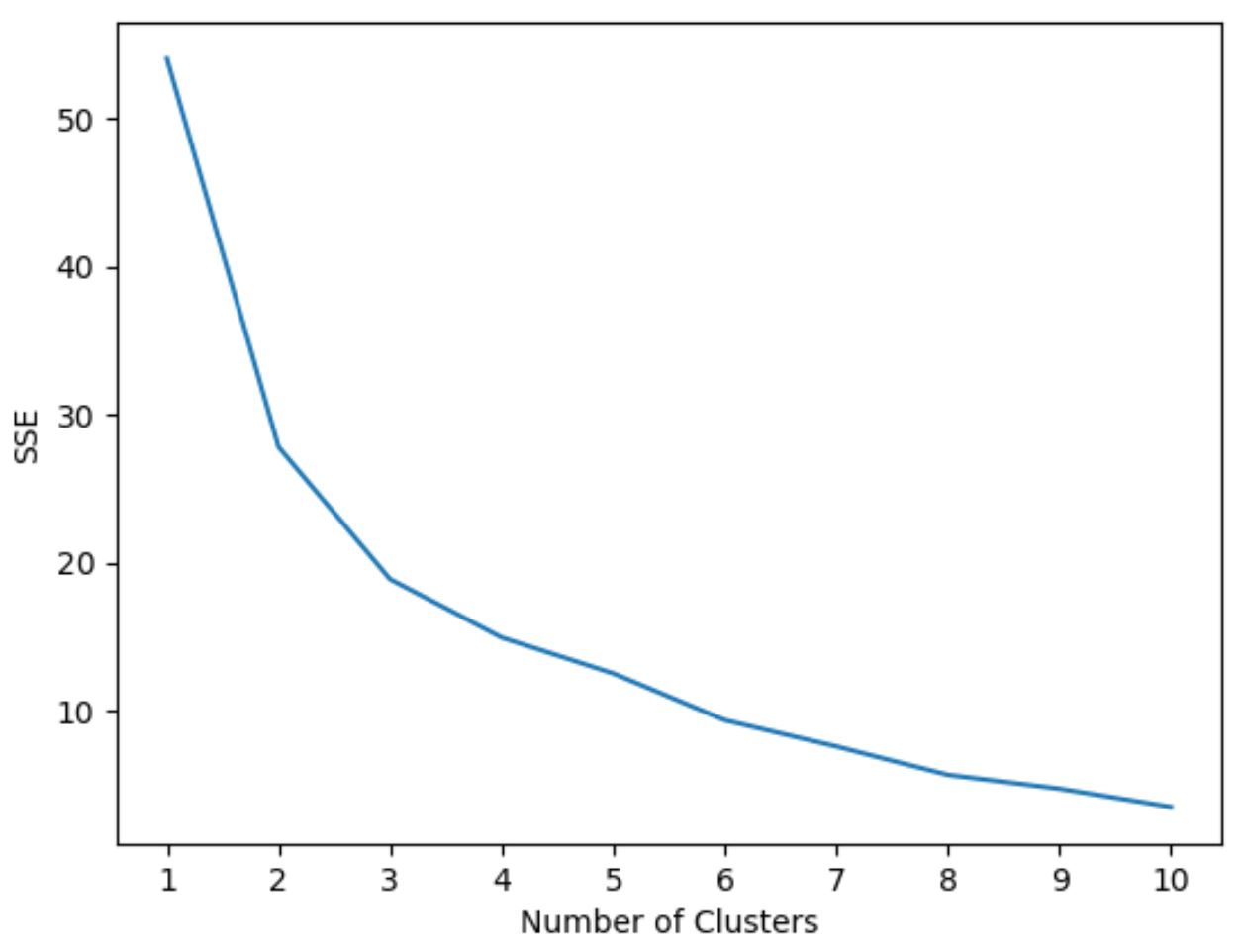
In diesem Diagramm scheint es, dass es bei k = 3 Clustern einen Knick oder ein „Knie“ gibt.

Daher werden wir im nächsten Schritt 3 Cluster verwenden, wenn wir unser k-Means-Clustering-Modell anpassen.

Hinweis : In der realen Welt wird empfohlen, eine Kombination aus diesem Plot- und Domänenwissen zu verwenden, um die Anzahl der zu verwendenden Cluster auszuwählen.

Schritt 5: Führen Sie K-Means-Clustering mit optimalem K durch

Der folgende Code zeigt, wie man k-Means-Clustering für den Datensatz unter Verwendung des optimalen Werts für k von 3 durchführt:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

Die resultierende Tabelle zeigt die Clusterzuweisungen für jede Beobachtung im DataFrame.

Um die Interpretation dieser Ergebnisse zu erleichtern, können wir dem DataFrame eine Spalte hinzufügen, die die Clusterzuweisung jedes Spielers anzeigt:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

Die Cluster- Spalte enthält eine Cluster-Nummer (0, 1 oder 2), der jeder Spieler zugewiesen wurde.

Spieler, die demselben Cluster angehören, haben ungefähr ähnliche Werte für die Spalten Punkte , Assists und Rebounds .

Hinweis : Die vollständige Dokumentation für die KMeans- Funktion von sklearn finden Sie hier .

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie Sie andere häufige Aufgaben in Python ausführen:

So führen Sie eine lineare Regression in Python durch
So führen Sie eine logistische Regression in Python durch
So führen Sie eine K-Fold-Kreuzvalidierung in Python durch