Kann kurtosis negativ sein?

In der Statistik wird Kurtosis verwendet, um die Form einer Wahrscheinlichkeitsverteilung zu beschreiben.

Konkret sagt es uns, wie gut sich Datenwerte in den Enden oder an der Spitze einer Verteilung gruppieren.

Die Kurtosis einer Verteilung kann negativ, null oder positiv sein.

Null Kurtosis

Wenn eine Verteilung eine Kurtosis von 0 hat, dann ist sie gleich der Normalverteilung, die die folgende Glockenform hat:

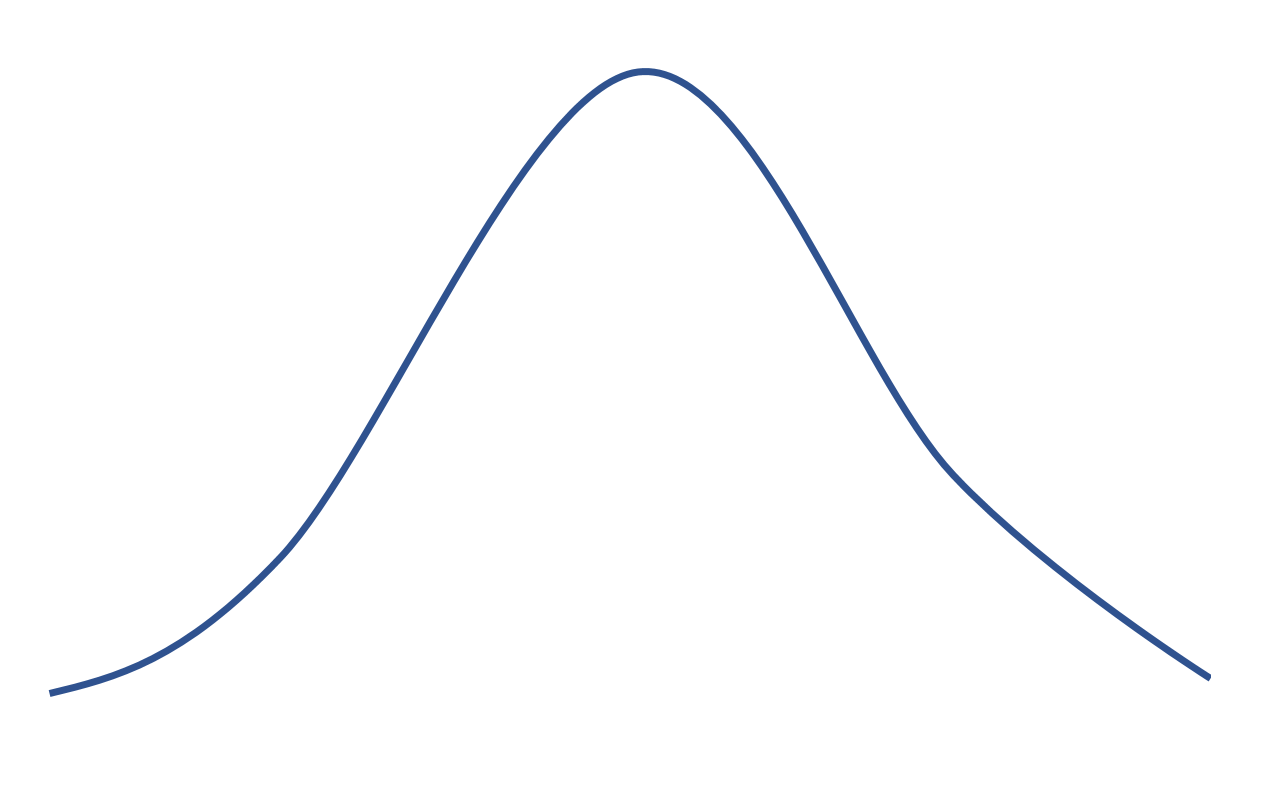
Positive Kurtosis

Wenn eine Verteilung eine positive Kurtosis aufweist, wird sie als leptokurtisch bezeichnet, was bedeutet, dass sie im Vergleich zu einer Normalverteilung eine schärfere Spitze und schwerere Enden aufweist.

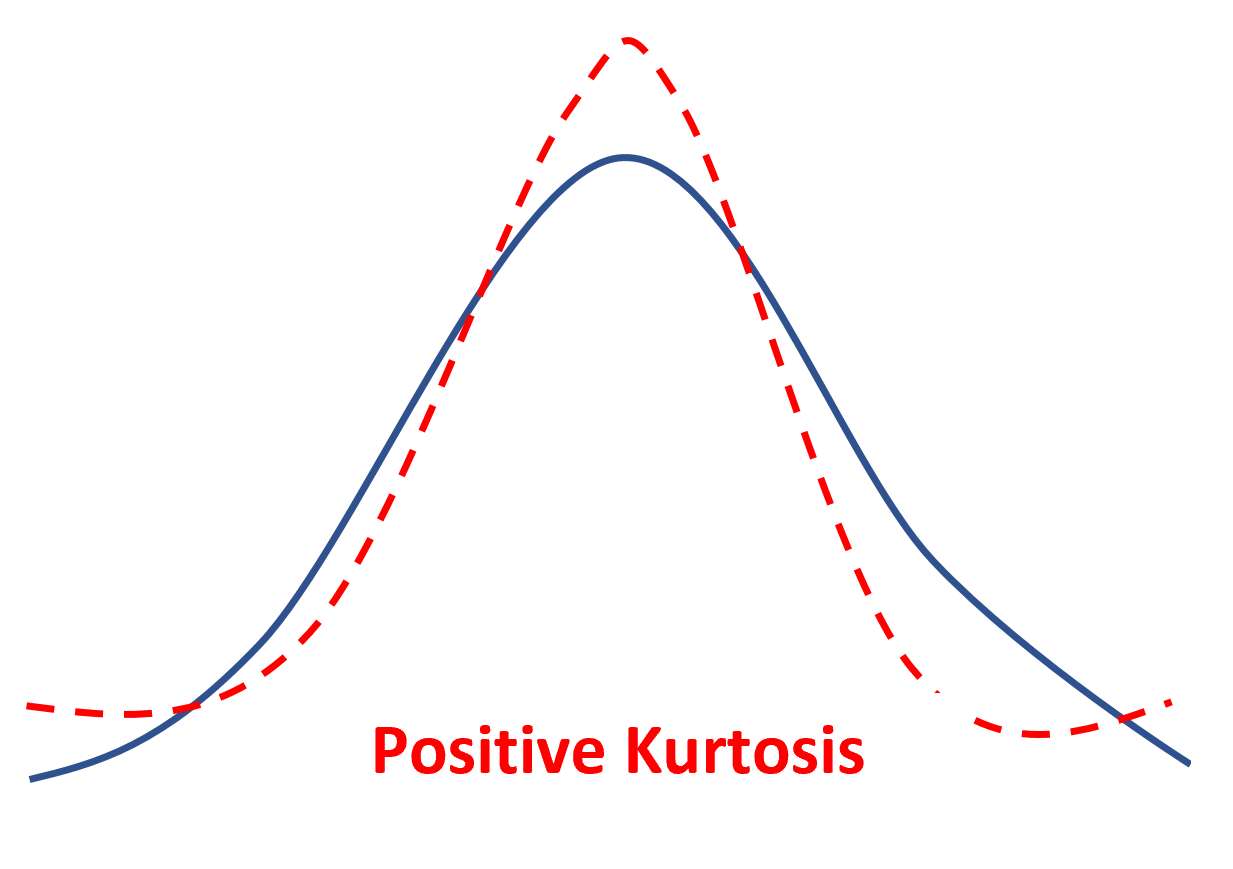
Dies bedeutet einfach, dass sich weniger Datenwerte in der Nähe des Mittelwerts und mehr Datenwerte an den Enden befinden.

Die bekannteste Verteilung mit positiver Kurtosis ist die t-Verteilung, die im Vergleich zur Normalverteilung eine schärfere Spitze und schwerere Enden aufweist.

Negative Kurtosis

Wenn eine Verteilung eine negative Kurtosis aufweist, wird sie als platykurtisch bezeichnet, was bedeutet, dass sie im Vergleich zu einer Normalverteilung eine flachere Spitze und dünnere Enden aufweist.

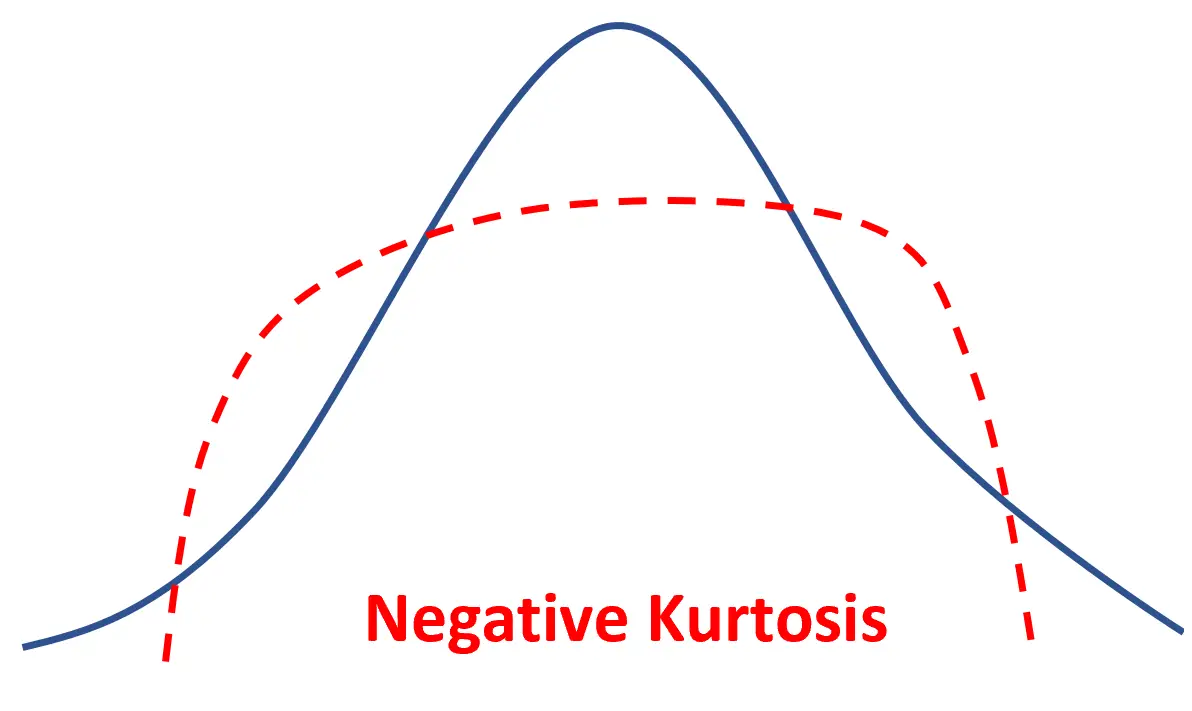
Dies bedeutet einfach, dass sich mehr Datenwerte in der Nähe des Mittelwerts und weniger Datenwerte an den Enden befinden.

Ein extremes Beispiel für eine Verteilung mit negativer Kurtosis ist die Gleichverteilung , die keine Spitzen aufweist und eine völlig flache Verteilung ist.

Wann man Schmeichelei in der Praxis einsetzen sollte

In der Praxis messen wir die Kurtosis einer Verteilung oft in der explorativen Analysephase, wenn wir einfach versuchen, die Daten besser zu verstehen.

Wenn wir also sehen, dass die Kurtosis positiv ist, wissen wir, dass wir mit einer Verteilung arbeiten, bei der sich weniger Datenwerte in der Nähe der Mitte befinden und mehr Datenwerte entlang der Enden verteilt sind.

Wenn wir umgekehrt sehen, dass die Kurtosis negativ ist, wissen wir, dass wir mit einer Verteilung arbeiten, die mehr Datenwerte in der Nähe der Mitte und weniger Datenwerte in den Enden aufweist.

Zusätzliche Ressourcen

Um die Schiefe und Kurtosis einer bestimmten Verteilung zu ermitteln, können Sie die Rohdatenwerte in diesen Schiefe- und Kurtosis-Rechner eingeben , der Ihnen sowohl die Schiefe als auch die Kurtosis der Verteilung anzeigt.

Einer der beliebtesten statistischen Tests zur Bestimmung, ob eine bestimmte Verteilung Schiefe und Kurtosis aufweist, die einer Normalverteilung entsprechen, ist der Jarque-Bera-Test .

Die Khan Academy hat auch eine schöne Reihe von Videos , die beschreiben, wie man Verteilungsformen klassifiziert.