Was ist eine kategoriale verteilung?

Eine kategoriale Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die die Wahrscheinlichkeit beschreibt, dass eine Zufallsvariable einen Wert annimmt, der zu einer von K Kategorien gehört, wobei jede Kategorie einer Wahrscheinlichkeit zugeordnet ist.

Damit eine Verteilung als kategoriale Verteilung klassifiziert werden kann, muss sie die folgenden Kriterien erfüllen:

• Die Kategorien sind diskret.
• Es gibt zwei oder mehr mögliche Kategorien.
• Die Wahrscheinlichkeit, dass die Zufallsvariable in jeder Kategorie einen Wert annimmt, muss zwischen 0 und 1 liegen.
• Die Summe der Wahrscheinlichkeiten für alle Kategorien muss 1 ergeben.

Das offensichtlichste Beispiel einer kategorialen Verteilung ist die Verteilung der Ergebnisse, die mit dem Würfeln verbunden sind. Es gibt K = 6 mögliche Ergebnisse und die Wahrscheinlichkeit jedes Ergebnisses beträgt 1/6:

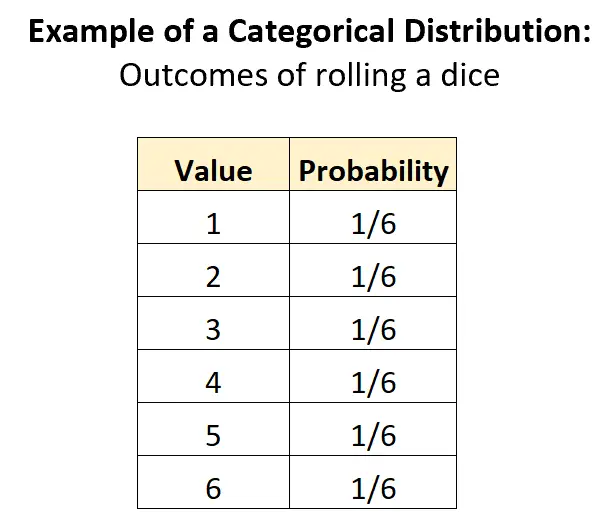
Diese Verteilung erfüllt alle Kriterien, um als kategoriale Verteilung klassifiziert zu werden:

• Die Kategorien sind diskret (zum Beispiel kann die Zufallsvariable nur diskrete Werte annehmen – 1, 2, 3, 4, 5, 6)
• Es gibt zwei oder mehr mögliche Kategorien.
• Die Wahrscheinlichkeit jeder Kategorie liegt zwischen 0 und 1.
• Die Summe der Wahrscheinlichkeiten beträgt 1: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Allgemeine Regel:

Wenn Sie die Anzahl der Ergebnisse zählen können, dann arbeiten Sie mit einer diskreten Zufallsvariablen – zum Beispiel zählen Sie, wie oft eine Münze „Kopf“ zeigt.

Wenn Sie das Ergebnis jedoch messen können, arbeiten Sie mit einer kontinuierlichen Zufallsvariablen – zum Beispiel mit der Messung von Größe, Gewicht, Zeit usw.

Weitere Beispiele für kategoriale Verteilungen

In der realen Welt gibt es viele kategoriale Verteilungen, darunter:

Beispiel 1: Wirf eine Münze.

Wenn wir eine Münze werfen, gibt es zwei mögliche diskrete Ergebnisse, die Wahrscheinlichkeit jedes Ergebnisses liegt zwischen 0 und 1 und die Summe der Wahrscheinlichkeiten ist gleich 1:

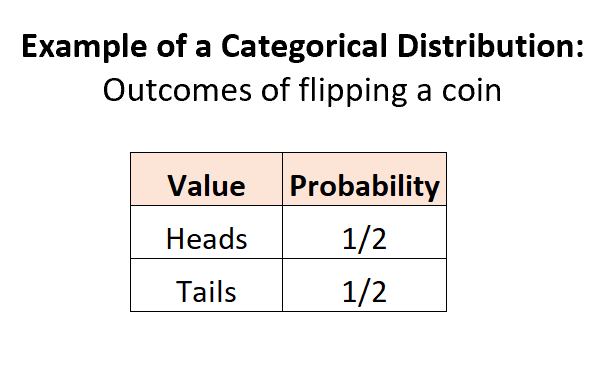
Beispiel 2: Auswahl von Murmeln in einer Urne.

Angenommen, eine Urne enthält 5 rote Murmeln, 3 grüne Murmeln und 2 violette Murmeln. Wenn wir zufällig eine Kugel aus der Urne auswählen, gibt es drei mögliche diskrete Ergebnisse, wobei die Wahrscheinlichkeit jedes Ergebnisses zwischen 0 und 1 liegt und die Summe der Wahrscheinlichkeiten gleich 1 ist:

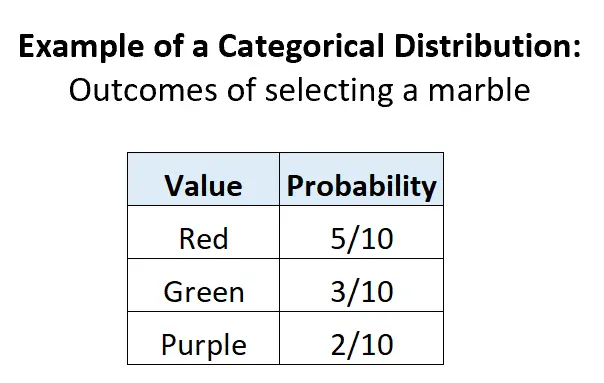
Beispiel 3: Eine Karte aus einem Stapel auswählen.

Wenn wir zufällig eine Karte aus einem Standardstapel mit 52 Karten auswählen, gibt es 13 mögliche diskrete Ergebnisse, die Wahrscheinlichkeit jedes Ergebnisses liegt zwischen 0 und 1 und die Summe der Wahrscheinlichkeiten beträgt 1:

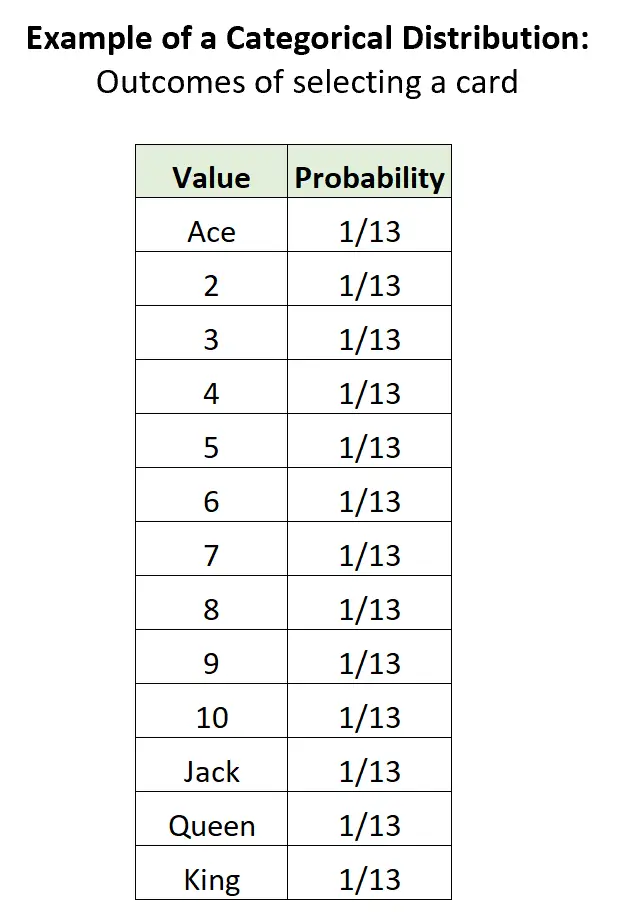
Beziehung zu anderen Distributionen

Damit eine Verteilung als kategoriale Verteilung klassifiziert werden kann, muss sie K ≥ 2 potenzielle Ergebnisse und n = 1 Versuch haben.

Unter Verwendung dieser Terminologie ähnelt eine kategoriale Verteilung den folgenden Verteilungen:

Bernoulli-Verteilung: K = 2 Ergebnisse, n = 1 Test

Binomialverteilung: K = 2 Endpunkte, n ≥ 1 Versuch

Multinomiale Verteilung: K ≥ 2 Ergebnisse, n ≥ Versuch

Zusätzliche Ressourcen

Was sind Zufallsvariablen?
Eine Einführung in die Binomialverteilung
Eine Einführung in die Multinomialverteilung