4 beispiele für mangelnde korrelation zwischen variablen

In der Statistik ist Korrelation ein Maß für den linearen Zusammenhang zwischen zwei Variablen.

Der Wert eines Korrelationskoeffizienten liegt immer zwischen -1 und 1, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Wenn zwei Variablen eine Korrelation von Null aufweisen, bedeutet dies, dass sie in keiner Weise miteinander verbunden sind. Mit anderen Worten: Wenn wir den Wert einer Variablen kennen, wissen wir nicht, welchen Wert die andere Variable haben könnte.

Wenn wir ein Streudiagramm zweier Variablen erstellen, die keine Korrelation aufweisen, ist im Diagramm kein klares Muster zu erkennen:

Beispiele für keine Korrelation

Die folgenden Beispiele veranschaulichen Szenarien, in denen zwei Variablen keine Korrelation aufweisen.

Beispiel 1: Kaffeekonsum versus Intelligenz

Die Menge des von Einzelpersonen konsumierten Kaffees und ihr IQ-Wert korrelieren nicht miteinander. Mit anderen Worten: Wenn wir wissen, wie viel Kaffee eine Person trinkt, können wir uns nicht ein Bild von ihrem IQ-Niveau machen.

Wenn wir ein Streudiagramm des täglichen Kaffeekonsums im Vergleich zum IQ-Level erstellen würden, würde es so aussehen:

Beispiel 2: Größe und Testergebnisse

Die Korrelation zwischen der Körpergröße der Schüler und ihren durchschnittlichen Testergebnissen beträgt Null. Mit anderen Worten: Die Kenntnis der Körpergröße einer Person gibt uns keinen Aufschluss über ihre durchschnittliche Prüfungspunktzahl.

Wenn wir ein Streudiagramm erstellen würden, das die Körpergröße im Vergleich zum durchschnittlichen Prüfungsergebnis darstellt, würde es so aussehen:

Beispiel 3: Schuhgröße und angesehene Filme

Die Schuhgröße von Personen und die Anzahl der Filme, die sie pro Jahr sehen, korrelieren nicht miteinander. Mit anderen Worten: Die Kenntnis der Schuhgröße einer Person gibt uns keinen Aufschluss darüber, wie viele Filme sie pro Jahr sieht.

Wenn wir ein Streudiagramm der Schuhgröße im Verhältnis zur Anzahl der angesehenen Filme erstellen würden, würde es so aussehen:

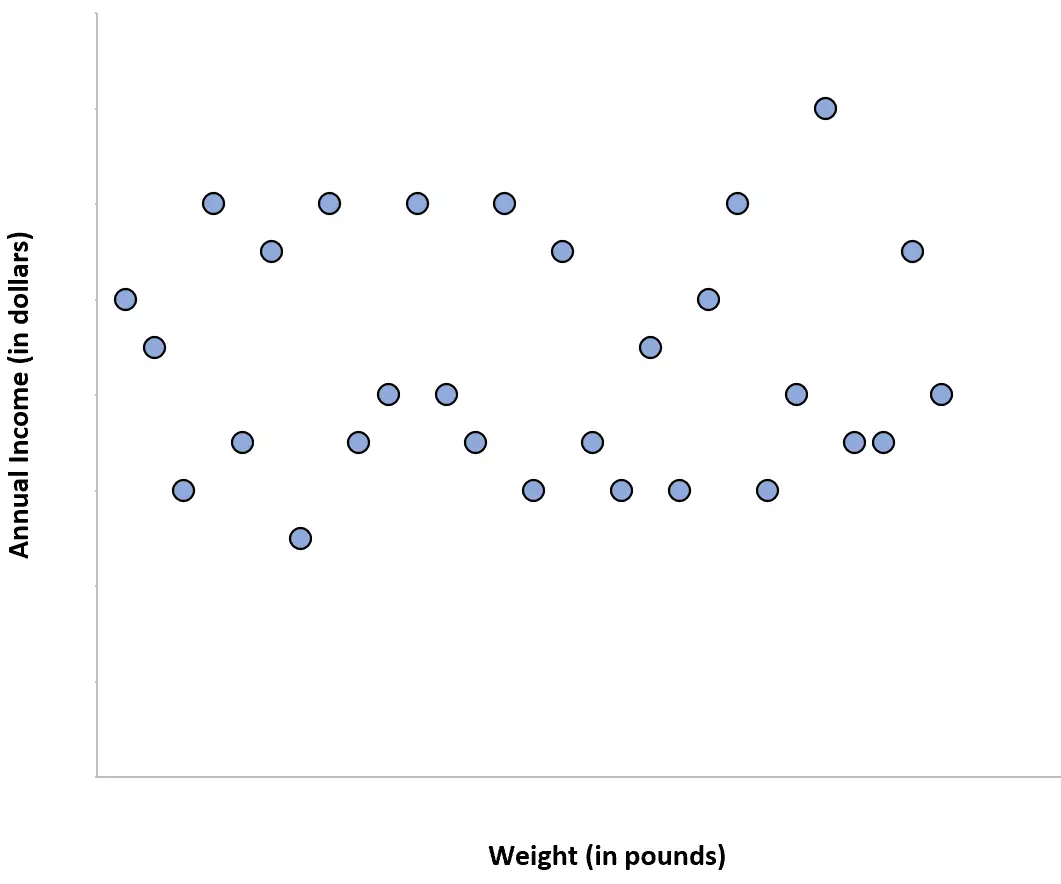
Beispiel 4: Gewicht und Einkommen

Das Gewicht der Personen und ihr Jahreseinkommen korrelieren nicht miteinander. Mit anderen Worten: Die Kenntnis des Gewichts einer Person gibt uns keine Vorstellung davon, wie hoch ihr Jahreseinkommen sein könnte.

Wenn wir ein Gewicht/Einkommen-Streudiagramm erstellen würden, würde es so aussehen:

Zusätzliche Ressourcen

Eine Einführung in den Pearson-Korrelationskoeffizienten
Korrelation vs. Assoziation: Was ist der Unterschied?
Korrelation vs. Regression: Was ist der Unterschied?