Kendalls tau: definition + beispiel

In der Statistik bezeichnet Korrelation die Stärke und Richtung einer Beziehung zwischen zwei Variablen. Der Wert eines Korrelationskoeffizienten kann zwischen -1 und 1 liegen, wobei -1 eine perfekte negative Beziehung angibt, 0 keine Beziehung angibt und 1 eine perfekte positive Beziehung angibt.

Der am häufigsten verwendete Korrelationskoeffizient ist der Pearson-Korrelationskoeffizient , der den linearen Zusammenhang zwischen zwei numerischen Variablen misst.

Ein weniger häufig verwendeter Korrelationskoeffizient ist Kendalls Tau , der die Beziehung zwischen zwei Spalten mit Rangdaten misst.

Die Formel zur Berechnung von Kendalls Tau, oft mit τ abgekürzt, lautet wie folgt:

τ = (CD) / (C+D)

Gold:

C = die Anzahl der passenden Paare

D = die Anzahl der diskordanten Paare

Das folgende Beispiel veranschaulicht, wie diese Formel zur Berechnung des Kendall-Tau-Rangkorrelationskoeffizienten für zwei Spalten mit Rangdaten verwendet wird.

Beispiel für die Berechnung von Kendalls Tau

Geht davon aus, dass zwei Basketballtrainer die 12 ihrer Spieler vom schlechtesten zum besten ordnen. Die folgende Tabelle zeigt die Ranglisten, die jeder Trainer den Spielern zugewiesen hat:

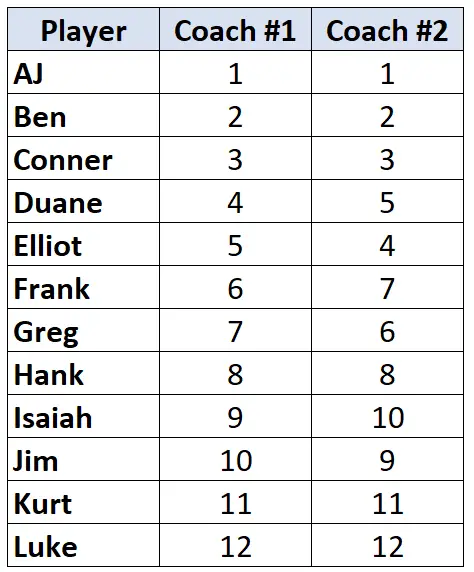
Da wir mit zwei Spalten mit Ranglistendaten arbeiten, ist es sinnvoll, Kendalls Tau zu verwenden, um die Korrelation zwischen den Ranglisten der beiden Trainer zu berechnen. Befolgen Sie die folgenden Schritte, um Kendalls Tau zu berechnen:

Schritt 1: Zählen Sie die Anzahl der passenden Paare.

Schauen Sie sich nur die Rangliste von Trainer Nr. 2 an. Zählen Sie beginnend mit dem ersten Spieler, um wie viele Ränge unter ihm der größere Spieler ist. Es gibt beispielsweise 11 Zahlen unter „1“, die größer sind, also schreiben wir 11:

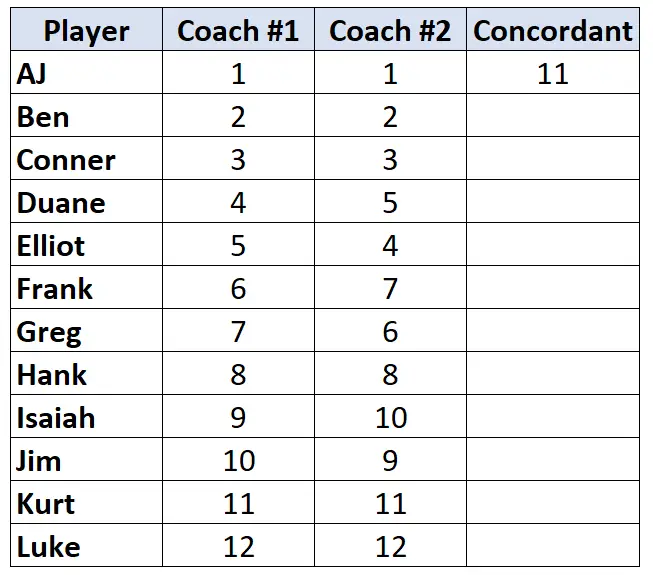
Gehen Sie zum nächsten Spieler und wiederholen Sie den Vorgang. Es gibt 10 Zahlen unter „2“, die größer sind, also schreiben wir 10:

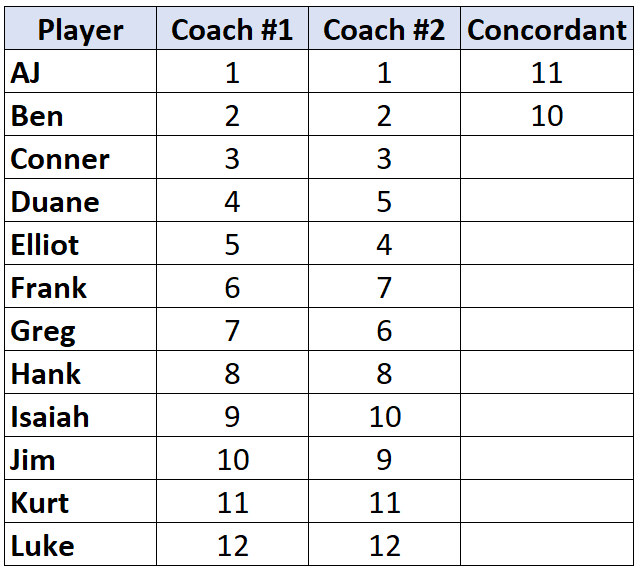
Sobald wir einen Spieler erreichen, dessen Rang niedriger ist als der des Spielers vor ihm, wird ihm einfach der gleiche Wert zugewiesen wie dem Spieler vor ihm. Elliot hat beispielsweise einen Rang von „4“, der niedriger ist als der Rang von „5“ des vorherigen Spielers, sodass ihm einfach der gleiche Wert wie dem Spieler vor ihm zugewiesen wird:

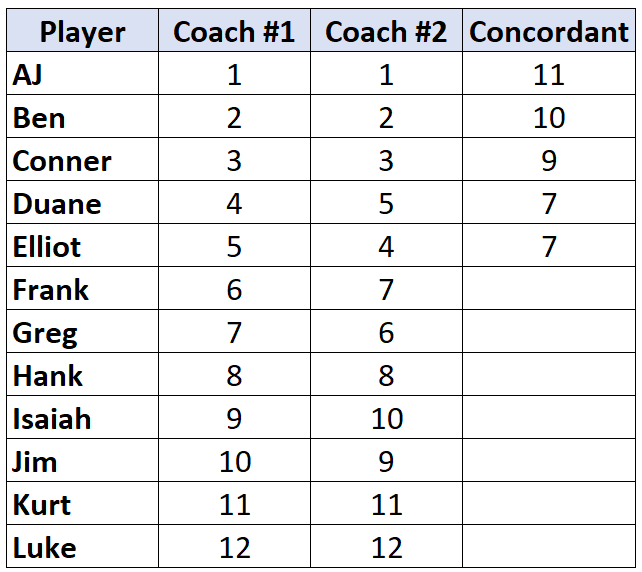
Wiederholen Sie diesen Vorgang für alle Spieler:

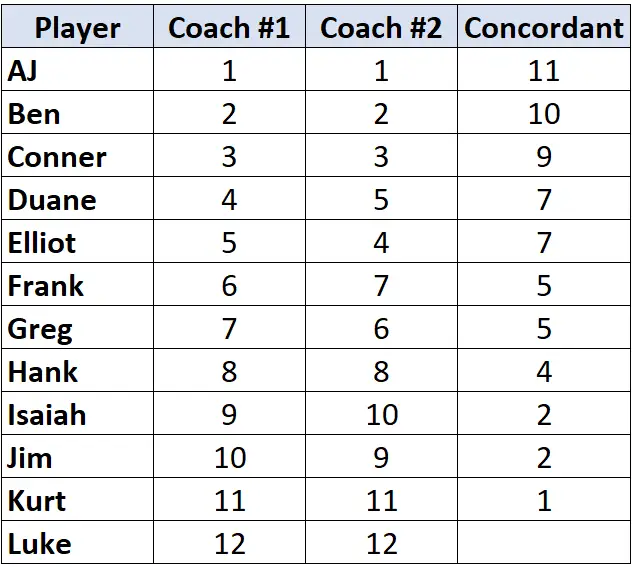
Schritt 2: Zählen Sie die Anzahl der nicht übereinstimmenden Paare.

Schauen Sie sich auch hier nur die Rangliste von Trainer Nr. 2 an. Zählen Sie für jeden Spieler, wie viele Ränge unter ihm kleiner sind. Beispielsweise hat Trainer Nr. 2 AJ den Rang „1“ zugewiesen und kein Spieler unter ihm hat einen niedrigeren Rang. Daher weisen wir ihm den Wert 0 zu:

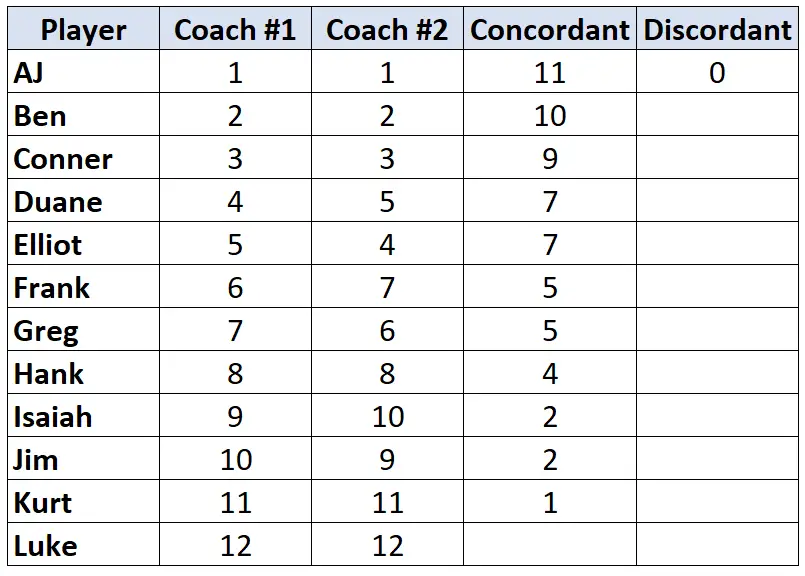
Wiederholen Sie diesen Vorgang für jeden Spieler:

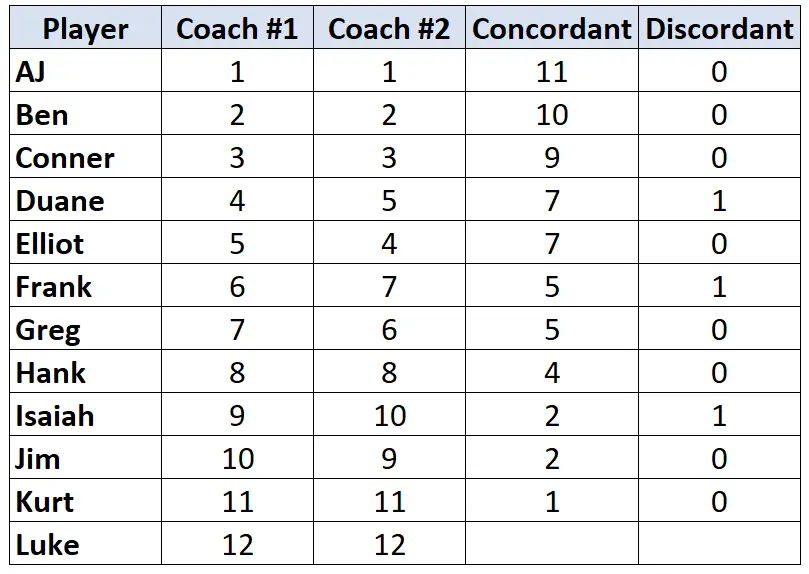
Schritt 3: Berechnen Sie die Summe jeder Spalte und ermitteln Sie Kendalls Tau.

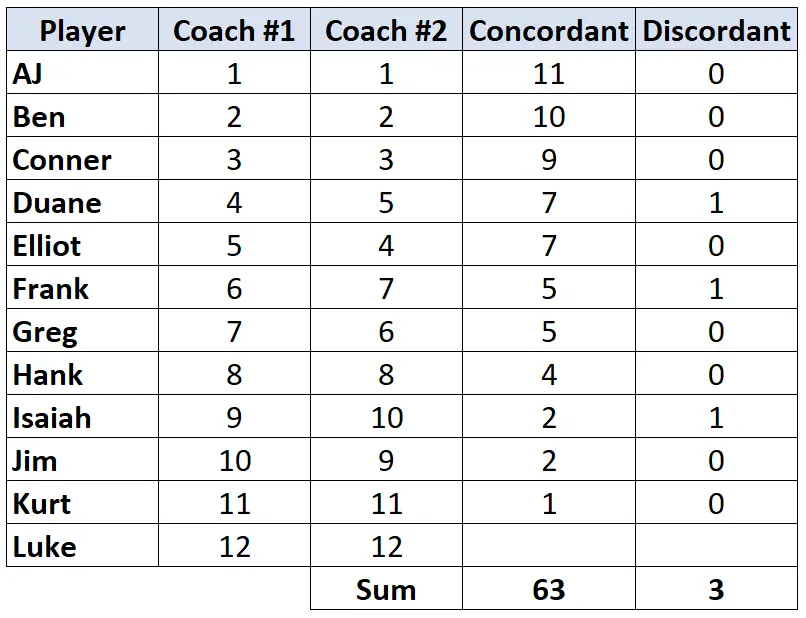
Kendalls Tau = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .

Statistische Bedeutung von Kendalls Tau

Wenn Sie mehr als n=10 Paare haben, folgt Kendalls Tau im Allgemeinen einer Normalverteilung. Sie können die folgende Formel verwenden, um einen Z-Score für Kendalls Tau zu berechnen:

z = 3τ*√ n(n-1) / √ 2(2n+5)

Gold:

τ = Wert, den Sie für Kendalls Tau berechnet haben

n = Anzahl der Paare

So berechnen Sie z für das vorherige Beispiel:

z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 .

Mithilfe des P-Wert-Z-Score-Rechners sehen wir, dass der p-Wert für diesen Z-Score 0,00004 beträgt, was auf dem Alpha-Niveau von 0,05 statistisch signifikant ist. Somit besteht eine statistisch signifikante Korrelation zwischen den Rängen, die die beiden Trainer den Spielern zugewiesen haben.

Bonus: So berechnen Sie Kendalls Tau in R

In der R-Statistiksoftware können Sie die Funktion kendall.tau() aus der VGAM-Bibliothek verwenden, um Kendalls Tau für zwei Vektoren zu berechnen, die die folgende Syntax verwendet:

kendall.tau(x, y)

wobei x und y zwei digitale Vektoren gleicher Länge sind.

Der folgende Code veranschaulicht, wie Kendalls Tau für die genauen Daten berechnet wird, die wir im vorherigen Beispiel verwendet haben:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

Beachten Sie, dass der Tau-Wert von Kendall mit dem Wert übereinstimmt, den wir manuell berechnet haben.