So passen sie klassifizierungs- und regressionsbäume in r an

Wenn die Beziehung zwischen einem Satz von Prädiktorvariablen und einer Antwortvariablen linear ist, können Methoden wie die multiple lineare Regression genaue Vorhersagemodelle erstellen.

Wenn jedoch die Beziehung zwischen einer Reihe von Prädiktoren und einer Reaktion komplexer ist, können nichtlineare Methoden häufig genauere Modelle erzeugen.

Eine solche Methode sind Klassifizierungs- und Regressionsbäume (CART), die eine Reihe von Prädiktorvariablen verwendet, um Entscheidungsbäume zu erstellen, die den Wert einer Antwortvariablen vorhersagen.

Wenn die Antwortvariable kontinuierlich ist, können wir Regressionsbäume erstellen, und wenn die Antwortvariable kategorisch ist, können wir Klassifizierungsbäume erstellen.

In diesem Tutorial wird erklärt, wie man Regressions- und Klassifizierungsbäume in R erstellt.

Beispiel 1: Erstellen eines Regressionsbaums in R

Für dieses Beispiel verwenden wir den Hitters- Datensatz aus dem ISLR- Paket, der verschiedene Informationen zu 263 professionellen Baseballspielern enthält.

Wir werden diesen Datensatz verwenden, um einen Regressionsbaum zu erstellen, der die Prädiktorvariablen von Homeruns und gespielten Jahren verwendet, um das Gehalt eines bestimmten Spielers vorherzusagen.

Führen Sie die folgenden Schritte aus, um diesen Regressionsbaum zu erstellen.

Schritt 1: Laden Sie die erforderlichen Pakete.

Zuerst laden wir die notwendigen Pakete für dieses Beispiel:

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Schritt 2: Erstellen Sie den ersten Regressionsbaum.

Zunächst erstellen wir einen großen anfänglichen Regressionsbaum. Wir können garantieren, dass der Baum groß ist, indem wir einen kleinen Wert für cp verwenden, was für „Komplexitätsparameter“ steht.

Das bedeutet, dass wir weitere Aufteilungen des Regressionsbaums durchführen, solange das Gesamt-R-Quadrat des Modells mindestens um den durch cp angegebenen Wert zunimmt.

Anschließend verwenden wir die Funktion printcp(), um die Modellergebnisse auszudrucken:

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

Schritt 3: Beschneiden Sie den Baum.

Als nächstes beschneiden wir den Regressionsbaum, um den optimalen Wert für cp (den Komplexitätsparameter) zu finden, der zum niedrigsten Testfehler führt.

Beachten Sie, dass der optimale Wert für cp derjenige ist, der zum niedrigsten x-Fehler in der vorherigen Ausgabe führt, der den Fehler bei den Beobachtungen aus den Kreuzvalidierungsdaten darstellt.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

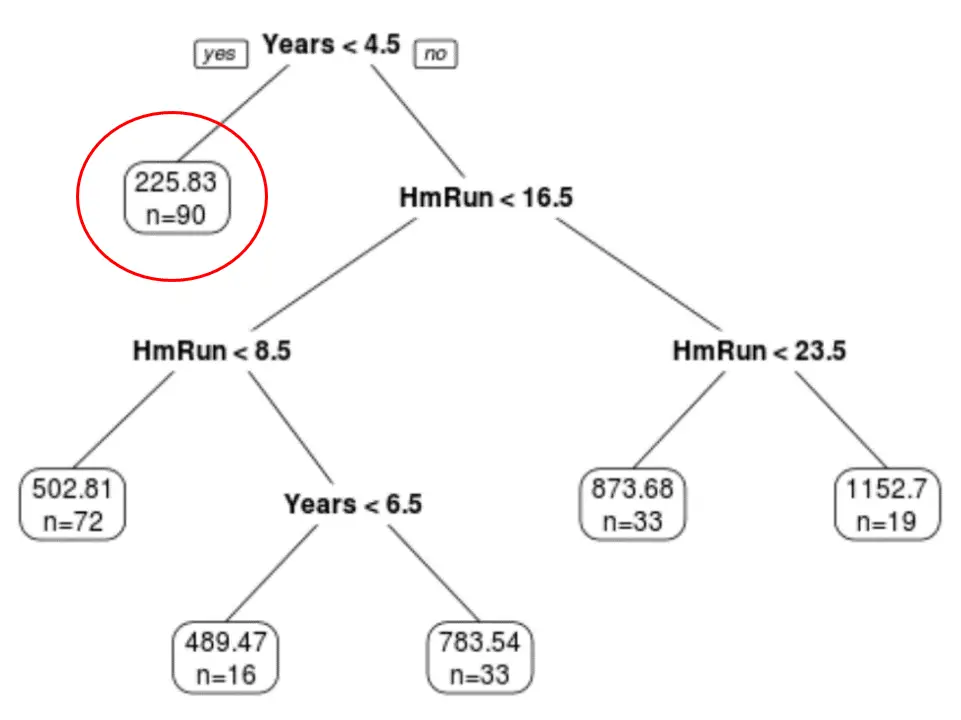
Wir können sehen, dass der endgültig beschnittene Baum sechs Endknoten hat. Jeder Blattknoten zeigt das vorhergesagte Gehalt der Spieler in diesem Knoten sowie die Anzahl der Beobachtungen aus dem Originaldatensatz an, die zu dieser Klasse gehören.

Wir können beispielsweise sehen, dass es im ursprünglichen Datensatz 90 Spieler mit weniger als 4,5 Jahren Erfahrung gab und ihr Durchschnittsgehalt 225,83.000 $ betrug.

Schritt 4: Verwenden Sie den Baum, um Vorhersagen zu treffen.

Wir können den endgültig beschnittenen Baum verwenden, um das Gehalt eines bestimmten Spielers basierend auf seiner jahrelangen Erfahrung und seinen durchschnittlichen Homeruns vorherzusagen.

Beispielsweise hat ein Spieler, der über 7 Jahre Erfahrung und durchschnittlich 4 Homeruns verfügt, ein erwartetes Gehalt von 502,81.000 $ .

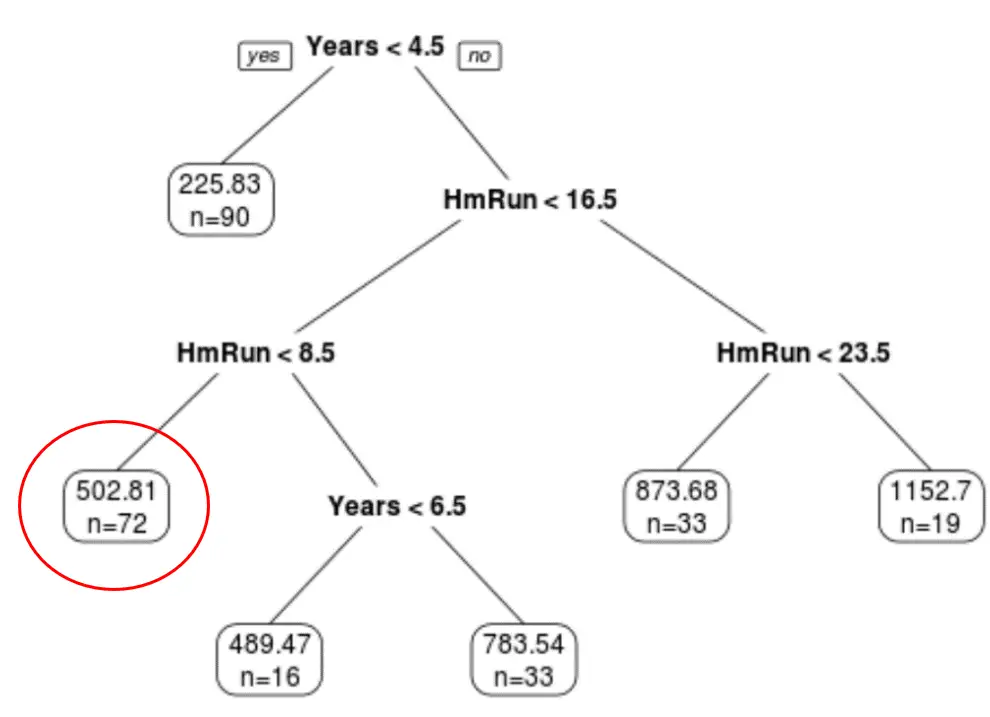
Wir können die Funktion „predict()“ in R verwenden, um dies zu bestätigen:

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

Beispiel 2: Erstellen eines Klassifizierungsbaums in R

Für dieses Beispiel verwenden wir den ptitanic- Datensatz aus dem Paket rpart.plot , der verschiedene Informationen über die Passagiere an Bord der Titanic enthält.

Wir werden diesen Datensatz verwenden, um einen Klassifizierungsbaum zu erstellen, der die Prädiktorvariablen Klasse , Geschlecht und Alter verwendet, um vorherzusagen, ob ein bestimmter Passagier überlebt hat oder nicht.

Führen Sie die folgenden Schritte aus, um diesen Klassifizierungsbaum zu erstellen.

Schritt 1: Laden Sie die erforderlichen Pakete.

Zuerst laden wir die notwendigen Pakete für dieses Beispiel:

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

Schritt 2: Erstellen Sie den anfänglichen Klassifizierungsbaum.

Zunächst erstellen wir einen großen anfänglichen Klassifizierungsbaum. Wir können garantieren, dass der Baum groß ist, indem wir einen kleinen Wert für cp verwenden, was für „Komplexitätsparameter“ steht.

Das bedeutet, dass wir weitere Aufteilungen des Klassifizierungsbaums durchführen, solange die Gesamtmodellanpassung mindestens um den durch cp angegebenen Wert zunimmt.

Anschließend verwenden wir die Funktion printcp(), um die Modellergebnisse auszudrucken:

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

Schritt 3: Beschneiden Sie den Baum.

Als Nächstes beschneiden wir den Regressionsbaum, um den optimalen Wert für cp (den Komplexitätsparameter) zu finden, der zum niedrigsten Testfehler führt.

Beachten Sie, dass der optimale Wert für cp derjenige ist, der zum niedrigsten x-Fehler in der vorherigen Ausgabe führt, der den Fehler bei den Beobachtungen aus den Kreuzvalidierungsdaten darstellt.

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

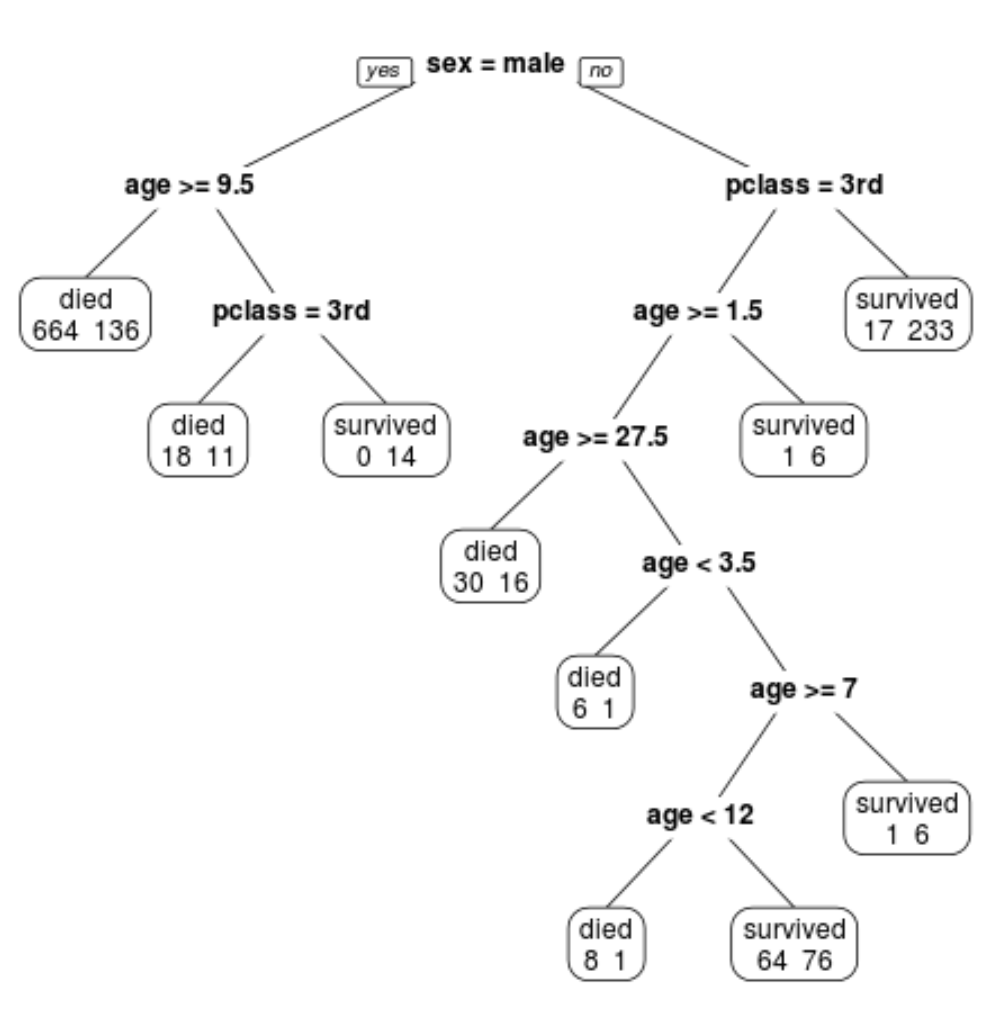
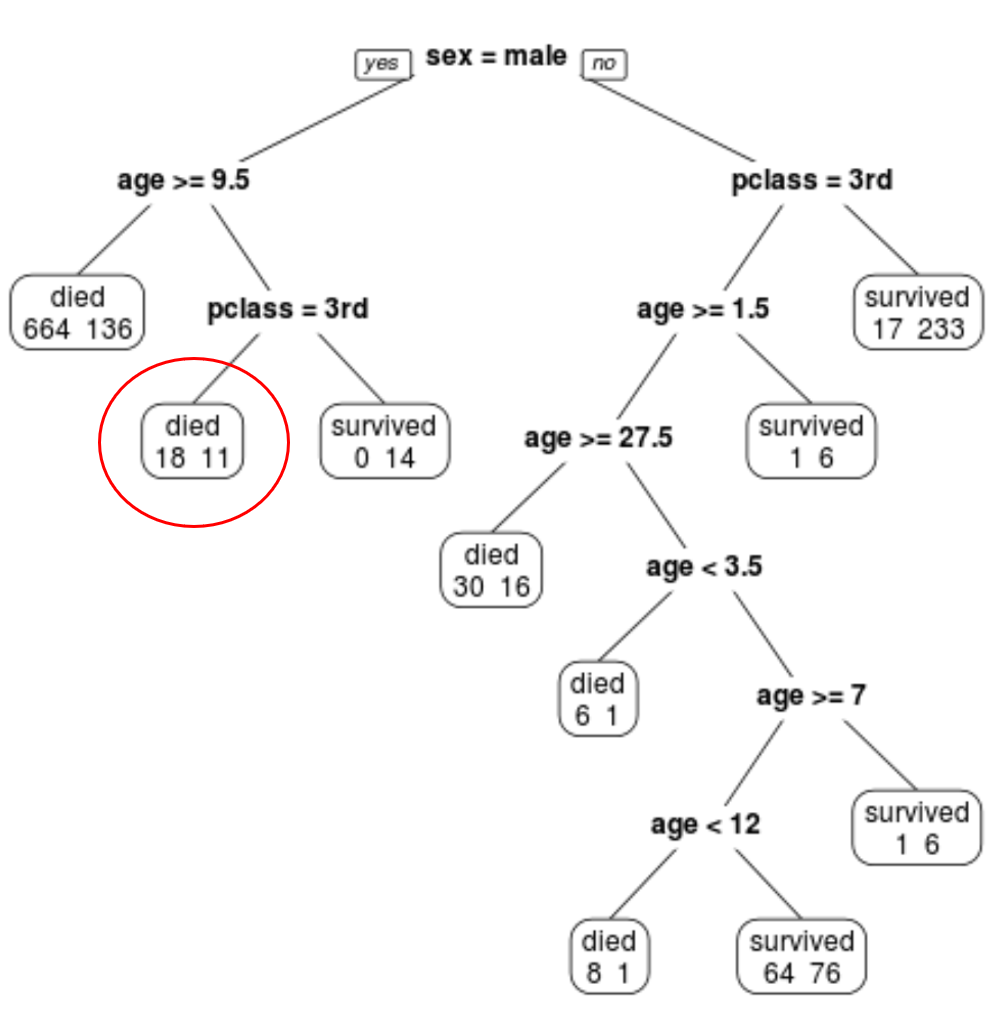
Wir können sehen, dass der endgültig beschnittene Baum 10 Endknoten hat. Jeder Endknoten gibt die Anzahl der verstorbenen Passagiere sowie die Anzahl der Überlebenden an.

Im Knoten ganz links sehen wir beispielsweise, dass 664 Passagiere starben und 136 überlebten.

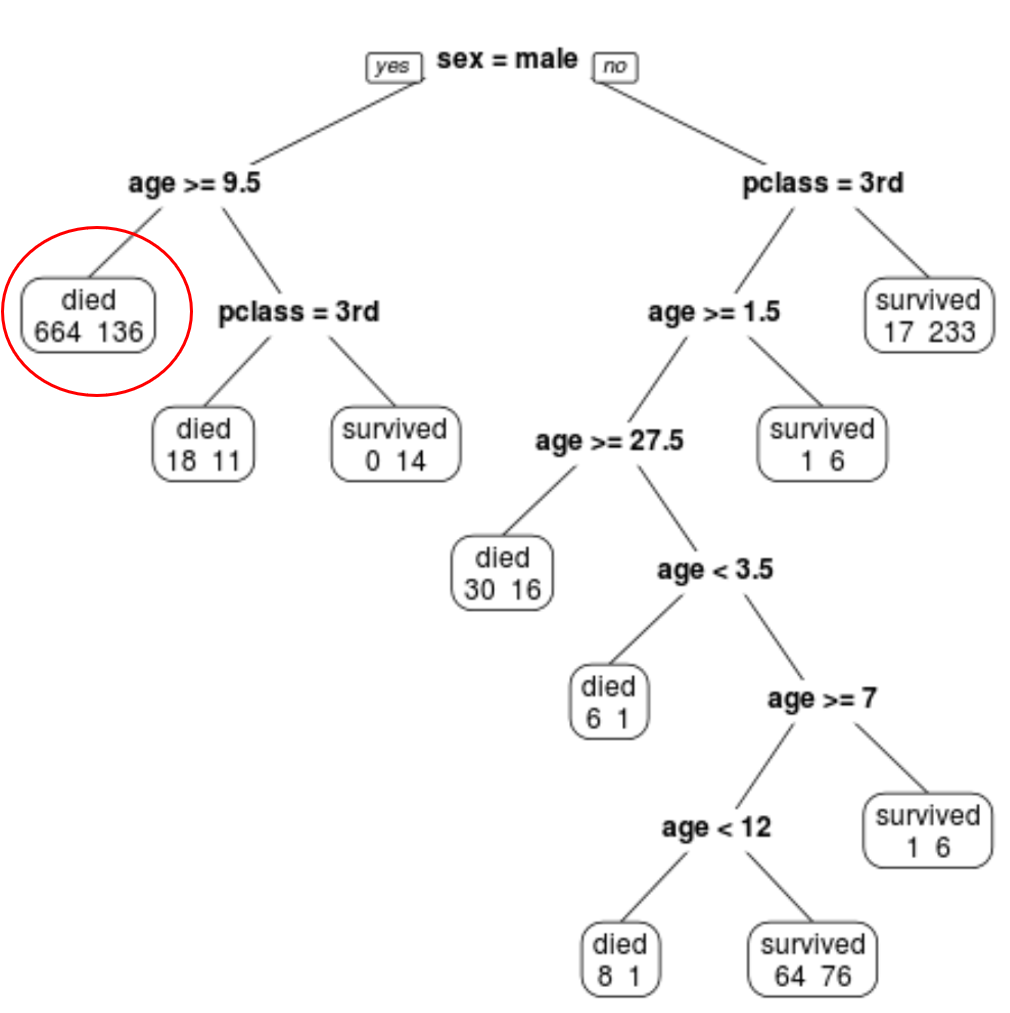
Schritt 4: Verwenden Sie den Baum, um Vorhersagen zu treffen.

Wir können den endgültig beschnittenen Baum verwenden, um die Überlebenswahrscheinlichkeit eines bestimmten Passagiers basierend auf seiner Klasse, seinem Alter und seinem Geschlecht vorherzusagen.

Beispielsweise hat ein männlicher Passagier im Alter von 8 Jahren und in der 1. Klasse eine Überlebenswahrscheinlichkeit von 11/29 = 37,9 %.

Den vollständigen R-Code, der in diesen Beispielen verwendet wird, finden Sie hier .