So erstellen sie ein konfidenzintervall mithilfe der f-verteilung

Um zu bestimmen, ob die Varianzen zweier Populationen gleich sind, können wir das Varianzverhältnis σ ² ₁ / σ ² ₂ berechnen, wobei σ ² ₁ die Varianz von Population 1 und σ ² ₂ die Varianz von Population 2 ist.

Um das wahre Populationsvarianzverhältnis zu schätzen, nehmen wir im Allgemeinen eine einfache Zufallsstichprobe aus jeder Population und berechnen das Stichprobenvarianzverhältnis s ₁ ² / s ₂ ² , wobei s ₁ ² und s ₂ ² die Stichprobenvarianzen für Stichprobe 1 und Stichprobe sind . 2 bzw.

Bei diesem Test wird davon ausgegangen, dass s ₁ ² und s ₂ ² aus unabhängigen Stichproben der Größe n ₁ und n ₂ berechnet werden, die beide aus normalverteilten Populationen stammen.

Je weiter dieses Verhältnis von eins entfernt ist, desto stärker sind die Hinweise auf ungleiche Varianzen innerhalb der Grundgesamtheit.

Das (1-α)100 %-Konfidenzintervall für σ ² ₁ / σ ² ₂ ist definiert als:

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1, α/2}

wobei F _{n 2 -1, n 1 -1, α/2} und F _{n 1 -1, n 2 -1, α/2}   sind die kritischen Werte der Verteilung F für das gewählte Signifikanzniveau α.

Die folgenden Beispiele veranschaulichen, wie man mit drei verschiedenen Methoden ein Konfidenzintervall für σ ² ₁ / σ ² ₂ erstellt:

• Durch die Hand
• Verwenden Sie Microsoft Excel
• Verwendung der Statistiksoftware R

Für jedes der folgenden Beispiele verwenden wir die folgenden Informationen:

• α = 0,05
• n ₁ = 16
• _n2 = 11
• s ₁ ² =28,2
• s ₂ ² = 19,3

Manuelles Erstellen eines Konfidenzintervalls

Um ein Konfidenzintervall für σ ² ₁ / σ ² ₂ manuell zu berechnen, fügen wir einfach die Zahlen, die wir haben, in die Konfidenzintervallformel ein:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

Die einzigen Zahlen, die uns fehlen, sind die kritischen Werte. Glücklicherweise können wir diese kritischen Werte in der Verteilungstabelle F finden:

F _{n2-1, n1-1, α/2} = F _{10, 15, 0,025} = 3,0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0,025} = 1 / 3,5217 = 0,2839

(Klicken Sie, um die Tabelle zu vergrößern)

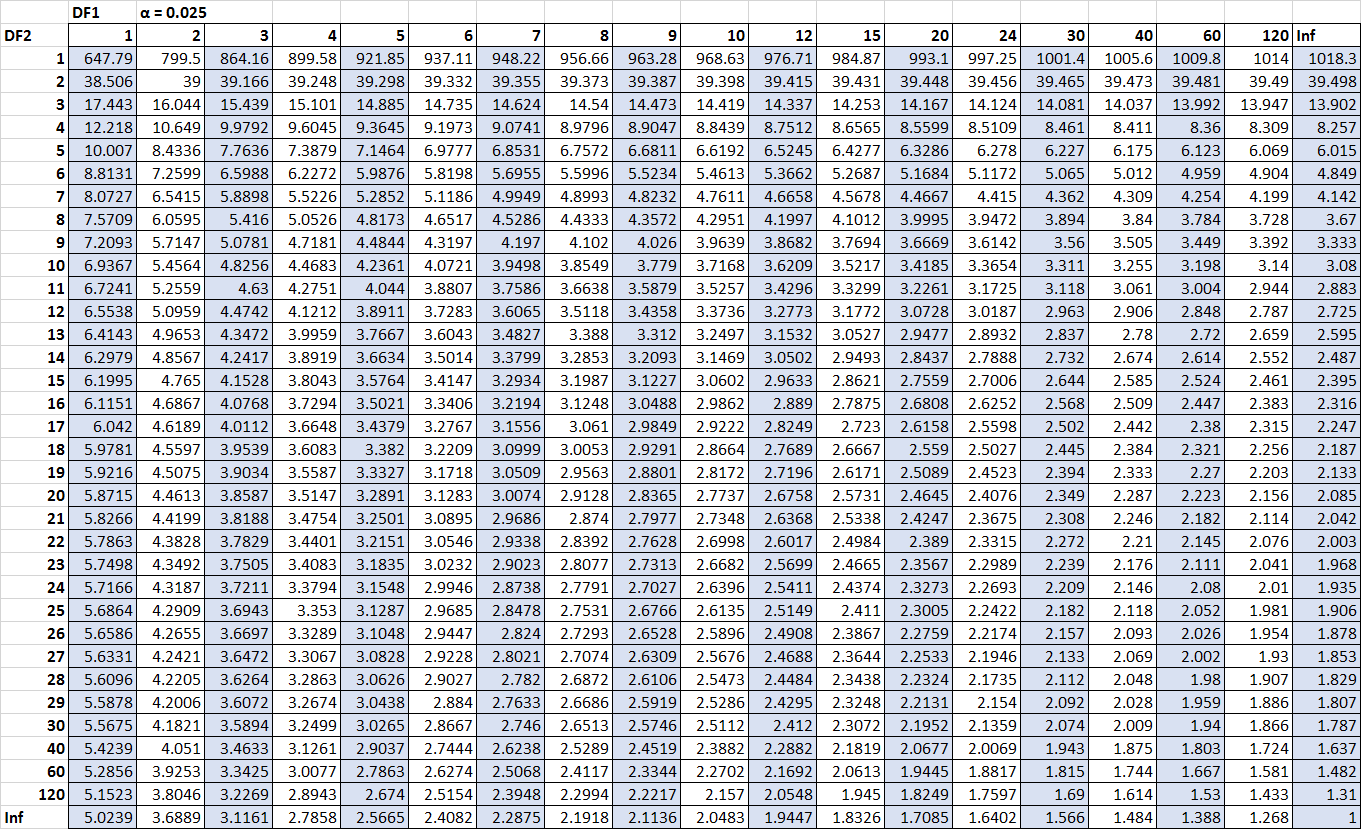
Wir können nun alle Zahlen in das Intervall der Konfidenzformel einfügen:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

(28,2 / 19,3) * (0,2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28,2 / 19,3) * (3,0602)

0,4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4,4714

Somit beträgt das 95 %-Konfidenzintervall für das Verhältnis der Populationsvarianzen (0,4148, 4,4714) .

Erstellen eines Konfidenzintervalls mit Excel

Die folgende Abbildung zeigt, wie ein 95 %-Konfidenzintervall für das Varianzverhältnis der Grundgesamtheit in Excel berechnet wird. Die Unter- und Obergrenzen des Konfidenzintervalls werden in Spalte E angezeigt und die Formel zur Ermittlung der Unter- und Obergrenzen wird in Spalte F angezeigt:

Somit beträgt das 95 %-Konfidenzintervall für das Verhältnis der Populationsvarianzen (0,4148, 4,4714) . Dies entspricht dem, was wir erhalten haben, als wir das Konfidenzintervall manuell berechnet haben.

Erstellen eines Konfidenzintervalls mit R

Der folgende Code veranschaulicht, wie ein 95 %-Konfidenzintervall für das Verhältnis der Populationsvarianzen in R berechnet wird:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

Somit beträgt das 95 %-Konfidenzintervall für das Verhältnis der Populationsvarianzen (0,4148, 4,4714) . Dies entspricht dem, was wir erhalten haben, als wir das Konfidenzintervall manuell berechnet haben.

Zusätzliche Ressourcen

So lesen Sie den F-Verteiler
So ermitteln Sie den kritischen Wert F in Excel