Konfidenzintervall für die differenz der mittelwerte
In diesem Artikel wird erläutert, was ein Konfidenzintervall für die Mittelwertdifferenz in der Statistik ist und wofür es verwendet wird. So erfahren Sie Schritt für Schritt, wie Sie das Konfidenzintervall für die Differenz zweier Mittelwerte berechnen und eine Übung lösen.
Was ist das Konfidenzintervall für die Differenz der Mittelwerte?
Das Konfidenzintervall für die Mittelwertdifferenz ist ein Intervall, das einen Maximalwert und einen Minimalwert angibt, zwischen denen der Wert der Mittelwertdifferenz zweier Grundgesamtheiten mit einem bestimmten Konfidenzniveau liegt.
Wenn beispielsweise das Konfidenzintervall für die Differenz der Mittelwerte zweier Grundgesamtheiten mit einem Konfidenzniveau von 95 % (3,5) beträgt, bedeutet dies, dass die Differenz zwischen den Mittelwerten der beiden Grundgesamtheiten mit einer Wahrscheinlichkeit von 95 zwischen 3 und 5 liegt %.
Daher wird in der Statistik das Konfidenzintervall für die Mittelwertdifferenz verwendet, um zwei Werte zu schätzen, zwischen denen die Differenz zweier Grundgesamtheitsmittelwerte liegt. Mithilfe von Daten aus zwei Stichproben ist es somit möglich, die Differenz zwischen den Grundgesamtheitsmittelwerten anzunähern.
Konfidenzintervallformel für Mittelwertunterschiede
Die Formel für das Konfidenzintervall für die Mittelwertdifferenz hängt davon ab, ob die Populationsvarianzen bekannt sind oder nicht und, falls nicht, ob die Populationsvarianzen als gleich angenommen werden können oder nicht. . Wir werden dann sehen, wie das Konfidenzintervall für die Mittelwertdifferenz jeweils berechnet wird.
bekannte Abweichungen
Die Formel zur Berechnung des Konfidenzintervalls für die Mittelwertdifferenz, wenn die Varianzen der beiden Grundgesamtheiten mit einem Konfidenzniveau von 1-α bekannt sind, lautet wie folgt:
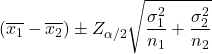
Gold:
-

ist der Mittelwert der Stichprobe i.
-

ist die Standardabweichung der Grundgesamtheit i.
-

ist der Wert der Standardnormalverteilung mit der Wahrscheinlichkeit α/2.
-

ist die Stichprobengröße i.
Dieser Fall kommt am seltensten vor, da der Wert der Populationsvarianzen im Allgemeinen unbekannt ist.
unbekannte und gleiche Varianzen
Wenn die Varianzen der beiden Populationen unbekannt sind, aber als gleich eingeschätzt werden können, lautet die Formel zur Berechnung des Konfidenzintervalls für die Mittelwertdifferenz mit einem Konfidenzniveau von 1-α wie folgt:
![]()
Gold:
-

ist der Mittelwert der Stichprobe i.
-

ist die gepoolte Standardabweichung.
-

ist der Wert der Student-t-Verteilung von n 1 + n 2 -2 Freiheitsgraden mit einer Wahrscheinlichkeit von α/2.
-

ist die Stichprobengröße i.
Da in diesem Fall davon ausgegangen wird, dass die Populationsvarianzen äquivalent sind, wird die kombinierte Standardabweichung zur Berechnung des Konfidenzintervalls verwendet, das mit der folgenden Formel berechnet wird:

Gold
![]()
ist die Standardabweichung der Probe i.
Unbekannte und unterschiedliche Variationen
Wenn die Varianzen der beiden Grundgesamtheiten unbekannt sind und nicht als gleich angenommen werden können, lautet die Formel zur Berechnung des Konfidenzintervalls für die Mittelwertdifferenz mit einem Konfidenzniveau von 1-α wie folgt:
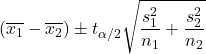
Gold:
-

ist der Mittelwert der Stichprobe i.
-
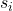
ist die Standardabweichung der Probe i.
-

ist der Wert der Student-t-Verteilung mit einer Wahrscheinlichkeit von α/2.
-

ist die Stichprobengröße i.
In diesem Fall werden die Freiheitsgrade der Student-t-Verteilung anhand der folgenden Formel berechnet:

Gold
![]()
ist die Standardabweichung der Probe i.
Konkretes Beispiel für das Konfidenzintervall für die Mittelwertdifferenz
Nachdem wir die Definition des Konfidenzintervalls für die Differenz der Mittelwerte und die verschiedenen Formeln kennengelernt haben, sehen wir uns nun ein konkretes Beispiel an, um zu verstehen, wie das Konfidenzintervall für die Differenz zweier Mittelwerte berechnet wird.
- Wir wollen den Einfluss von Tabak auf das Geburtsgewicht von Kindern untersuchen. Dazu werden zwei Stichproben verglichen: Die erste Stichprobe besteht aus Kindern, deren Mütter nicht geraucht haben, und die zweite Stichprobe besteht aus Kindern, deren Mütter geraucht haben (die Stichprobenparameter sind unten angegeben). Berechnen Sie das Konfidenzintervall für die Mittelwertdifferenz mit einem Konfidenzniveau von 95 %.
- Nichtrauchermütter:
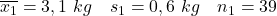
- Rauchende Mütter:
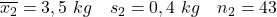
- Nichtrauchermütter:
In diesem Fall kennen wir die Werte der Populationsvarianzen nicht, können jedoch davon ausgehen, dass die Populationsvarianzen äquivalent sind, da es sich um zwei Populationen mit sehr ähnlichen Merkmalen handelt. Daher lautet die Formel für das Konfidenzintervall für die Mittelwertdifferenz, die wir verwenden sollten:
![]()
Daher berechnen wir die kombinierte Standardabweichung aus den Standardabweichungen der beiden Stichproben:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
Ebenso müssen wir den Wert der Student-t-Verteilung mit 80 Freiheitsgraden mit einer Wahrscheinlichkeit von 2,5 % in der Wahrscheinlichkeitsverteilungstabelle der Student-t-Verteilung finden:
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Abschließend setzen wir die Daten in die Konfidenzintervallformel für die Mittelwertdifferenz ein und führen die Berechnungen durch:
![]()
![]()
![]()
Das Konfidenzintervall für die Differenz der Mittelwerte des Problems ist daher wie folgt:
![]()