Konfidenzintervall für proportionen

Von Dr. Benjamin Anderson August 3, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erläutert, was das Konfidenzintervall für Proportionen ist und wofür es in der Statistik verwendet wird. Ebenso erfahren Sie, wie Sie das Konfidenzintervall des Anteils berechnen, sowie eine gelöste Übung zum besseren Verständnis des Konzepts.

Was ist das Konfidenzintervall des Anteils?

Das Konfidenzintervall für Anteile ist ein Intervall, das einen Bereich zulässiger Werte für den Anteil einer Grundgesamtheit angibt. Das heißt, das Konfidenzintervall für den Anteil gibt einen Maximalwert und einen Minimalwert an, zwischen denen der Bevölkerungsanteil mit einer Fehlermarge liegt.

Wenn beispielsweise das Konfidenzintervall für den Anteil einer Grundgesamtheit mit einem Konfidenzniveau von 95 % (0,73, 0,81) beträgt, bedeutet dies, dass der Anteil einer Grundgesamtheit mit einer Wahrscheinlichkeit von 95 % zwischen 73 % und 81 % liegt.

Daher wird das Konfidenzintervall des Anteils verwendet, um den Wert des Anteils einer Bevölkerung zu schätzen, der bestimmte Merkmale erfüllt.

Wie wir im nächsten Abschnitt sehen werden, hängt das Konfidenzintervall für den Anteil vom Stichprobenanteil und der Anzahl der Beobachtungen in der Stichprobe ab.

Konfidenzintervallformel für Proportionen

Das Konfidenzintervall für den Anteil wird berechnet, indem der Wert von Z _α/2 , multipliziert mit der Quadratwurzel des Stichprobenanteils (p), multipliziert mit 1-p, addiert und vom Stichprobenanteil subtrahiert und durch die Stichprobengröße (n) dividiert wird. Daher lautet die Formel zur Berechnung des Konfidenzintervalls für den Anteil :

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

Gold:

$p$

ist der Stichprobenanteil.
$n$

ist die Stichprobengröße.
$Z_{\alpha/2}$

ist das Quantil der Standardnormalverteilung, das einer Wahrscheinlichkeit von α/2 entspricht. Bei großen Stichprobengrößen und einem Konfidenzniveau von 95 % liegt er normalerweise nahe bei 1,96 und bei einem Konfidenzniveau von 99 % normalerweise nahe bei 2,576.

Beispiel für die Berechnung eines Konfidenzintervalls für Proportionen

Damit Sie sehen können, wie ein Konfidenzintervall für den Anteil berechnet wird, hinterlassen wir Ihnen im Folgenden ein konkretes Beispiel Schritt für Schritt.

Eine Versicherungsgesellschaft möchte Marktforschung betreiben und ermitteln, wie viele Menschen in einem Land eine Lebensversicherung haben. Dazu wird eine Stichprobe von 700 Personen analysiert und wir kommen zu dem Ergebnis, dass 40 % der Stichprobe über eine Lebensversicherung verfügen. Wie groß ist das Konfidenzintervall beim 95 %-Konfidenzniveau für den Anteil der Bevölkerung des Landes?

Um das Konfidenzintervall des Bevölkerungsanteils zu bestimmen, müssen wir die oben gesehene Formel verwenden:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

In diesem Fall soll das Konfidenzniveau des Konfidenzintervalls 95 % betragen, sodass der Wert von Z _α/2, den wir annehmen müssen, 1,96 beträgt.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Aus der Problemstellung geht bereits hervor, dass die Stichprobengröße n=700 beträgt und der beobachtete Anteil in der Stichprobe p=0,40 beträgt. Daher setzen wir die Daten für den Anteil in die Konfidenzintervallformel ein und berechnen die Grenzen des Intervalls:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

$\displaystyle \left(0,40-1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}}\ , \ 0,40+1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}\right)$

$\displaystyle \left(0,36 \ , \ 0,44\right)$

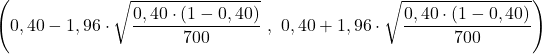
Zusammenfassend lässt sich sagen, dass der Anteil der untersuchten Bevölkerung zwischen 36 % und 44 % liegt, mit einem Konfidenzniveau von 95 %.

➤ Siehe: Konfidenzintervall für den Mittelwert
➤ Siehe: Konfidenzintervall für Varianz

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Was ist das Konfidenzintervall des Anteils?

Konfidenzintervallformel für Proportionen

Beispiel für die Berechnung eines Konfidenzintervalls für Proportionen

Über den Autor

Dr. Benjamin Anderson

Einen Kommentar hinzufügen