Excel: berechnen sie das konfidenzintervall für den regressionskoeffizienten

In einem linearen Regressionsmodell gibt uns ein Regressionskoeffizient die durchschnittliche Änderung der Antwortvariablen an, die mit einem Anstieg der Prädiktorvariablen um eine Einheit verbunden ist.

Mit der folgenden Formel können wir ein Konfidenzintervall für einen Regressionskoeffizienten berechnen:

Konfidenzintervall für β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

Gold:

•   b ₁ = In der Regressionstabelle angezeigter Regressionskoeffizient
• t _{1-∝/2, n-2} = Der kritische t-Wert für das 1-∝-Konfidenzniveau mit n-2 Freiheitsgraden, wobei n die Gesamtzahl der Beobachtungen in unserem Datensatz ist
• se(b ₁ ) = Der in der Regressionstabelle angezeigte Standardfehler von b ₁

Das folgende Beispiel zeigt, wie ein Konfidenzintervall für einen Regressionskoeffizienten in Excel berechnet wird.

Beispiel: Konfidenzintervall für Regressionskoeffizienten in Excel

Angenommen, wir möchten ein einfaches lineares Regressionsmodell anpassen, indem wir die untersuchten Stunden als Prädiktorvariable und Prüfungsergebnisse als Antwortvariable für 15 Schüler in einer bestimmten Klasse verwenden:

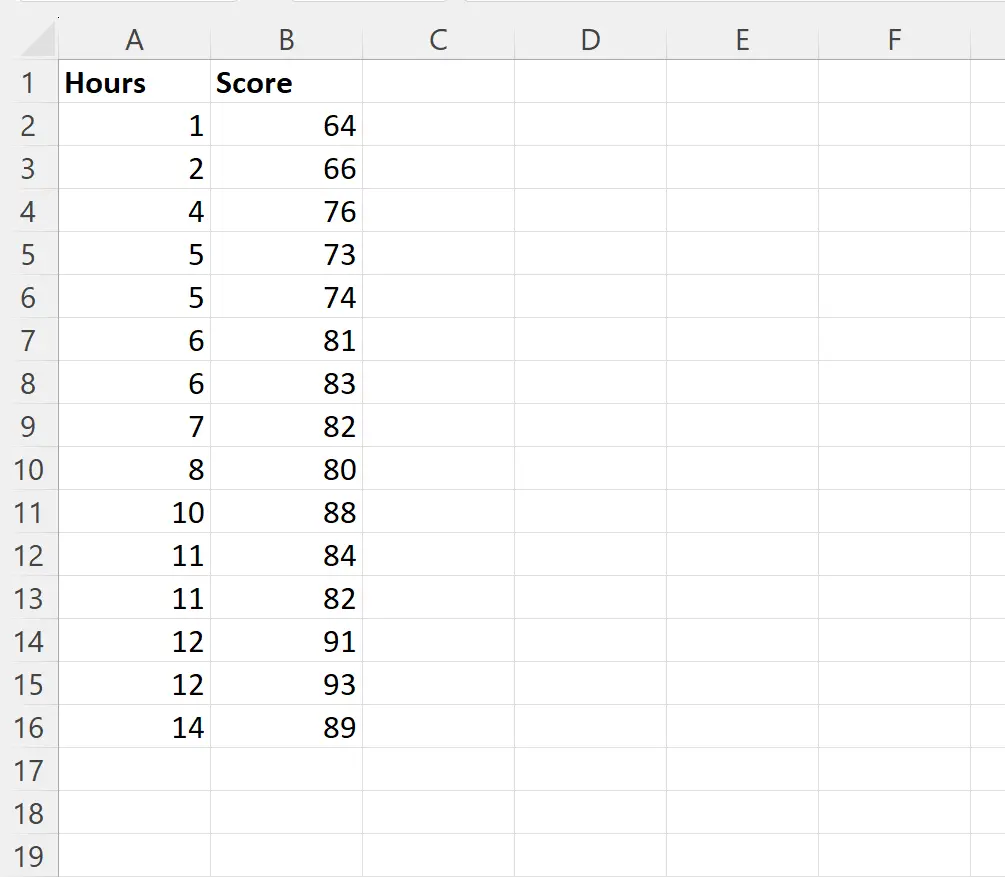
Wir können die folgende Formel in Zelle D2 eingeben, um eine einfache lineare Regression durchzuführen, indem wir die Werte in der Spalte „ Stunden “ als Prädiktorvariable und die Werte in der Spalte „Punktzahl“ als Antwortvariable verwenden:

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

Beachten Sie, dass das erste TRUE- Argument Excel anweist, den Achsenabschnitt der Regressionsgleichung normal zu berechnen, ohne ihn auf Null zu zwingen.

Das zweite TRUE- Argument weist Excel an, zusätzlich zu den Koeffizienten zusätzliche Regressionsstatistiken zu erstellen.

Der folgende Screenshot zeigt das Ergebnis dieser Formel (wir erklären, was jeder Ausgabewert im roten Text unter der Ausgabe darstellt):

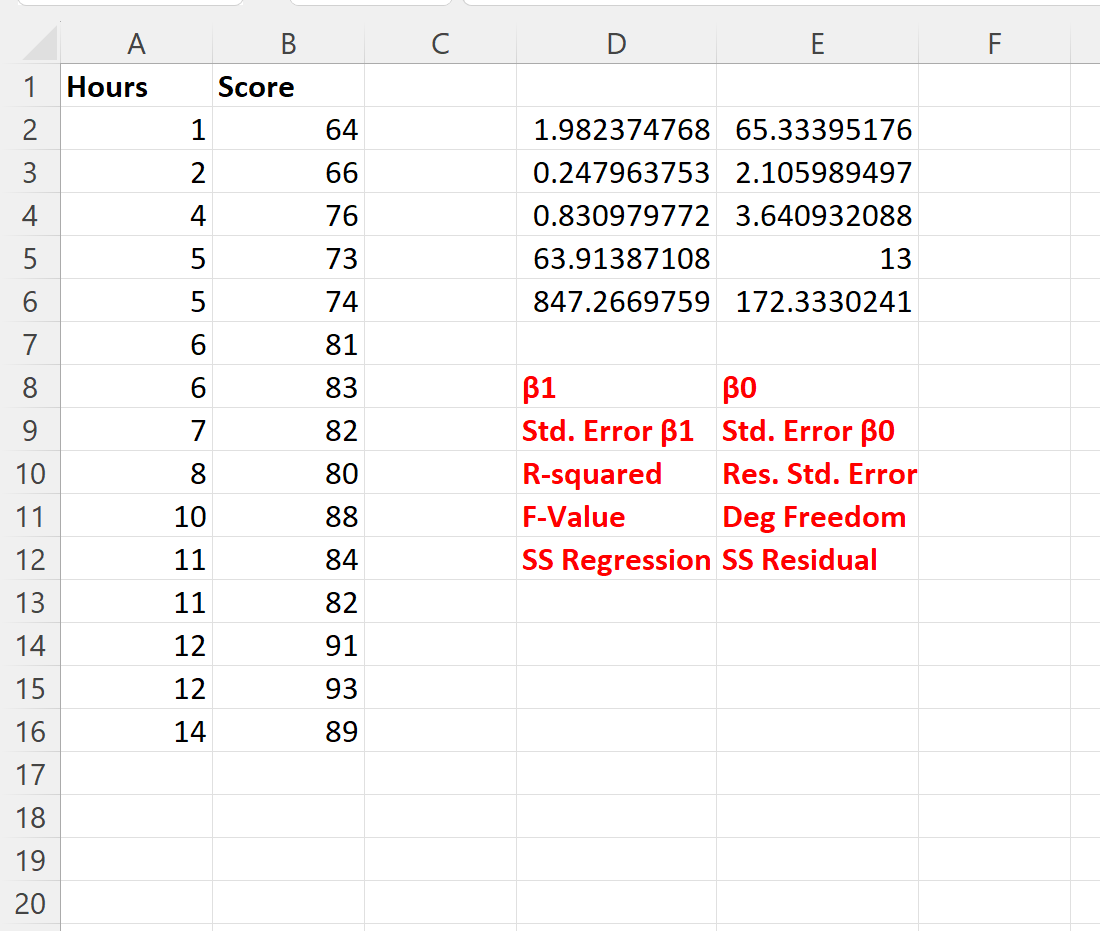
Unter Verwendung der Regressionskoeffizienten können wir die angepasste Regressionsgleichung wie folgt schreiben:

Punktzahl = 65,334 + 1,982*(Studienstunden)

Beachten Sie, dass der Regressionskoeffizient für Stunden 1,982 beträgt.

Dies zeigt uns, dass jede zusätzliche Stunde Lernzeit mit einer durchschnittlichen Steigerung der Prüfungspunktzahl um 1.982 verbunden ist.

Um ein 95 %-Konfidenzintervall für den Regressionskoeffizienten zu berechnen, können wir die folgenden Formeln in die Zellen H2 und H3 eingeben:

• H2: = D2 – T.INV.2T(0,05, E5)*D3
• H3: = D2 + T.INV.2T(0,05, E5)*D3

Der folgende Screenshot zeigt, wie diese Formeln in der Praxis angewendet werden:

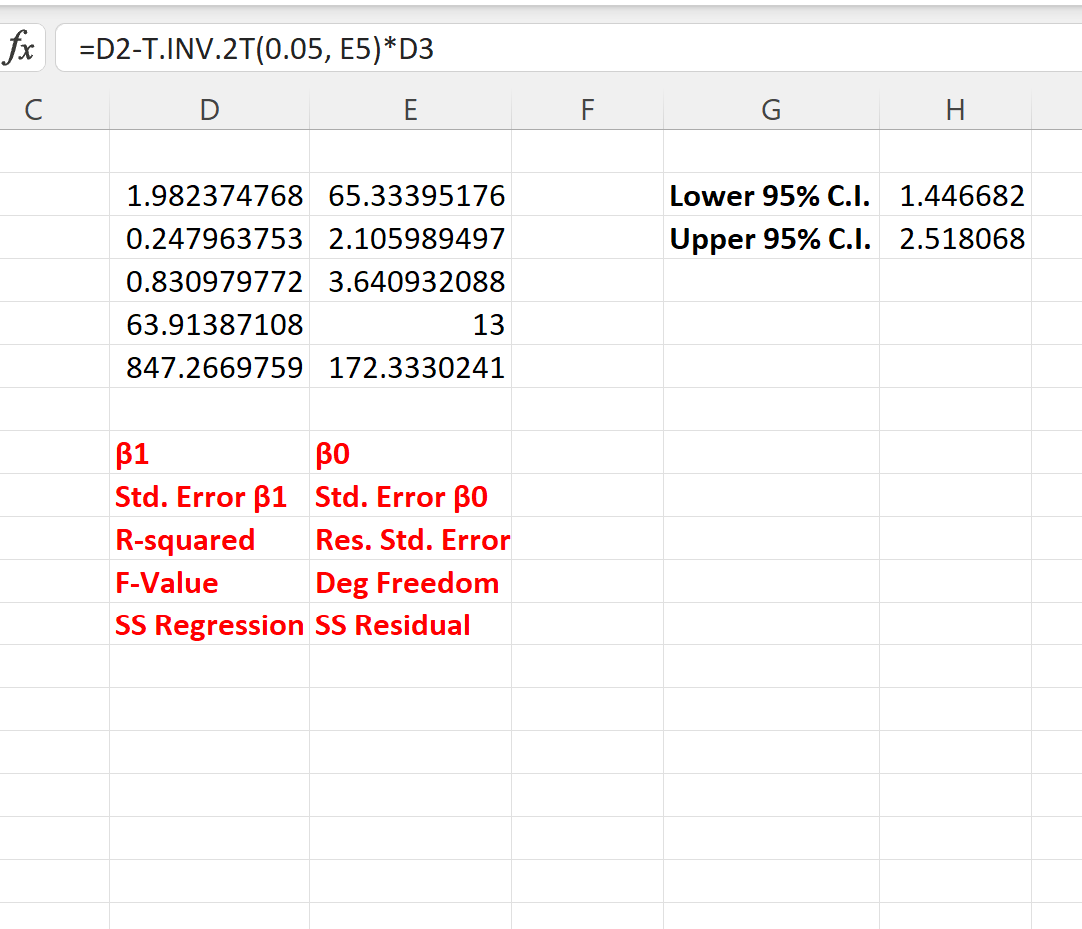
Das 95 %-Konfidenzintervall für den Regressionskoeffizienten beträgt [1,446, 2,518] .

Da dieses Konfidenzintervall nicht den Wert 0 enthält , können wir daraus schließen, dass ein statistisch signifikanter Zusammenhang zwischen den gelernten Stunden und der Prüfungsnote besteht.

Wir können auch bestätigen, dass dies richtig ist, indem wir das 95 %-Konfidenzintervall für den Regressionskoeffizienten manuell berechnen:

• 95 %-KI für β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• 95 %-KI für β ₁ : 1,982 ± t _{0,975, 15-2} * 0,248
• 95 %-KI für β ₁ : 1,982 ± 2,1604 * 0,248
• 95 %-KI für β ₁ : [1,446, 2,518]

Das 95 %-Konfidenzintervall für den Regressionskoeffizienten beträgt [1,446, 2,518] .

Zusätzliche Ressourcen

In den folgenden Tutorials wird erklärt, wie Sie andere häufige Aufgaben in Excel ausführen:

So führen Sie eine einfache lineare Regression in Excel durch
So führen Sie eine multiple lineare Regression in Excel durch
So interpretieren Sie P-Werte in der Regressionsausgabe in Excel