So berechnen sie konfidenzintervalle in google sheets

Ein Konfidenzintervall für einen Mittelwert ist ein Wertebereich, der wahrscheinlich einen Populationsmittelwert mit einem bestimmten Konfidenzniveau enthält.

Es wird wie folgt berechnet:

Konfidenzintervall = x +/- t*(s/√ n )

Gold:

• x : Stichprobenmittel
• t: t-Wert, der dem Konfidenzniveau entspricht
• s: Stichprobenstandardabweichung
• n: Stichprobengröße

In diesem Tutorial wird erklärt, wie man Konfidenzintervalle in Google Sheets berechnet.

Konfidenzintervalle unter Verwendung der t-Verteilung

Wenn wir mit einer kleinen Stichprobe (n < 30) arbeiten, können wir die t-Verteilung verwenden, um ein Konfidenzintervall für einen Grundgesamtheitsmittelwert zu berechnen.

Angenommen, wir möchten anhand einer Stichprobe von 15 Pflanzen ein Konfidenzintervall für die tatsächliche durchschnittliche Populationshöhe (in Zoll) einer bestimmten Pflanzenart berechnen:

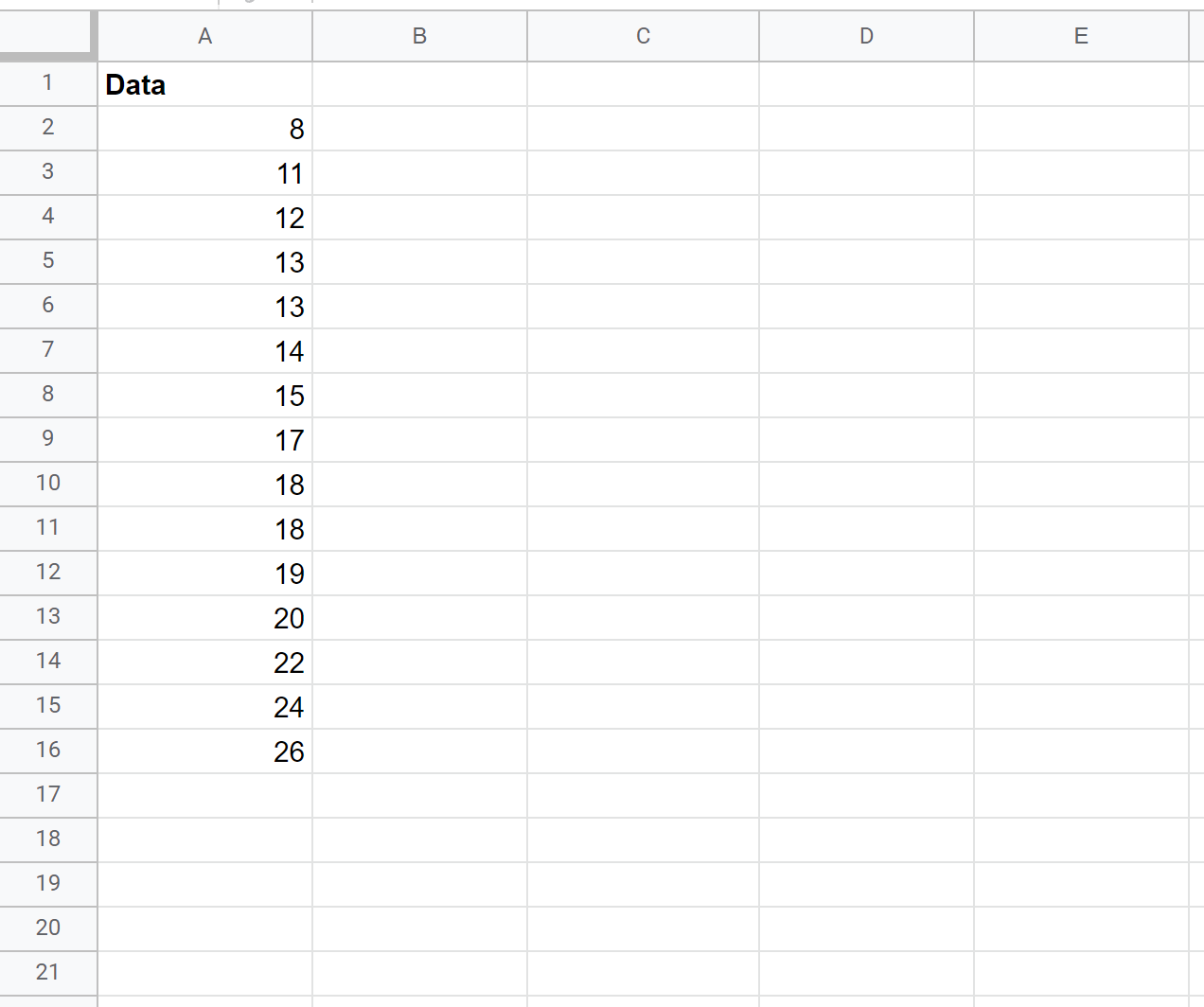
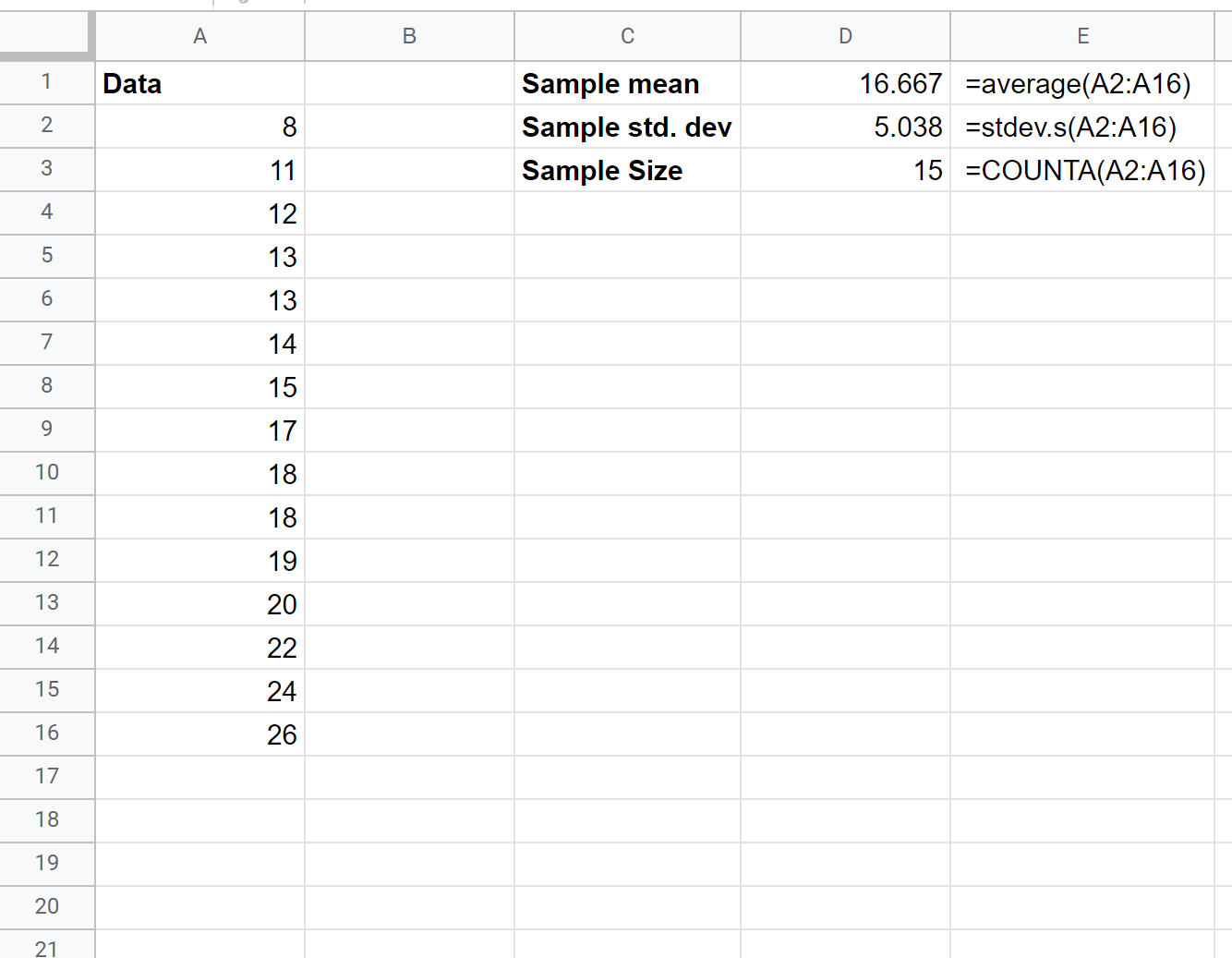
Zunächst können wir den Stichprobenmittelwert, die Stichprobenstandardabweichung und die Stichprobengröße berechnen:

Dann können wir die folgenden Formeln verwenden, um die untere und obere Grenze des 95 %-Konfidenzintervalls zu berechnen:

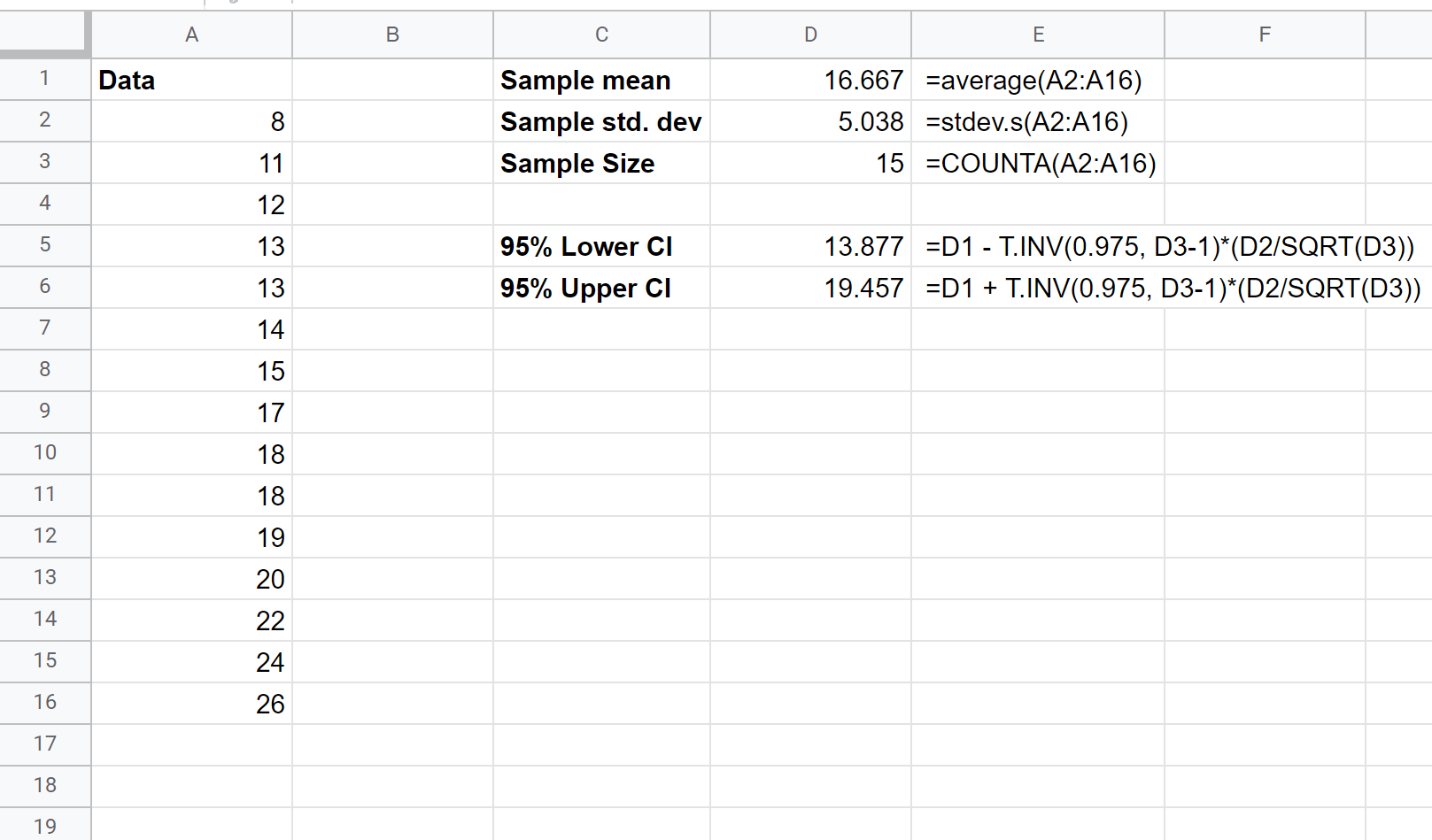
Das 95 %-Konfidenzintervall für die tatsächliche mittlere Bevölkerungsgröße beträgt (13,877, 19,457) .

Konfidenzintervalle unter Verwendung der Normalverteilung

Wenn wir mit größeren Stichproben (n≥30) arbeiten, können wir dank des zentralen Grenzwertsatzes davon ausgehen, dass die Stichprobenverteilung des Stichprobenmittelwerts normalverteilt ist.

Das bedeutet, dass wir stattdessen die Funktion NORM.S.INV() verwenden können, um den kritischen Wert zu berechnen, der für das Konfidenzintervall verwendet werden soll.

Das folgende Beispiel zeigt, wie ein Konfidenzintervall für die tatsächliche durchschnittliche Populationshöhe (in Zoll) einer bestimmten Pflanzenart anhand einer Stichprobe von 30 Pflanzen berechnet wird:

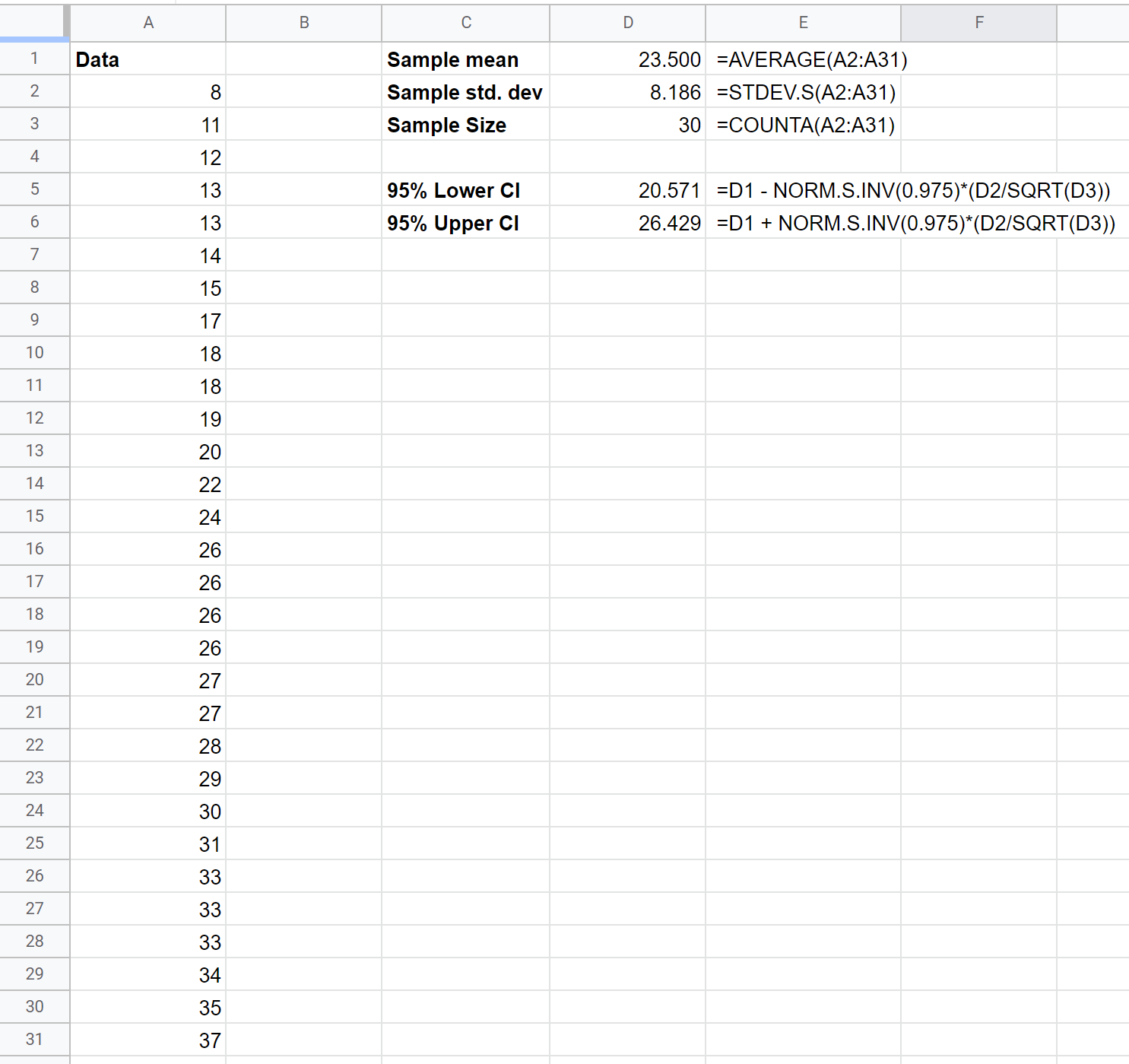
Das 95 %-Konfidenzintervall für die tatsächliche mittlere Bevölkerungsgröße beträgt (20,571, 26,429) .

Beachten Sie, dass höhere Konfidenzniveaus zu größeren Konfidenzintervallen führen. So berechnen Sie beispielsweise ein 99 %-KI für genau dieselben Daten:

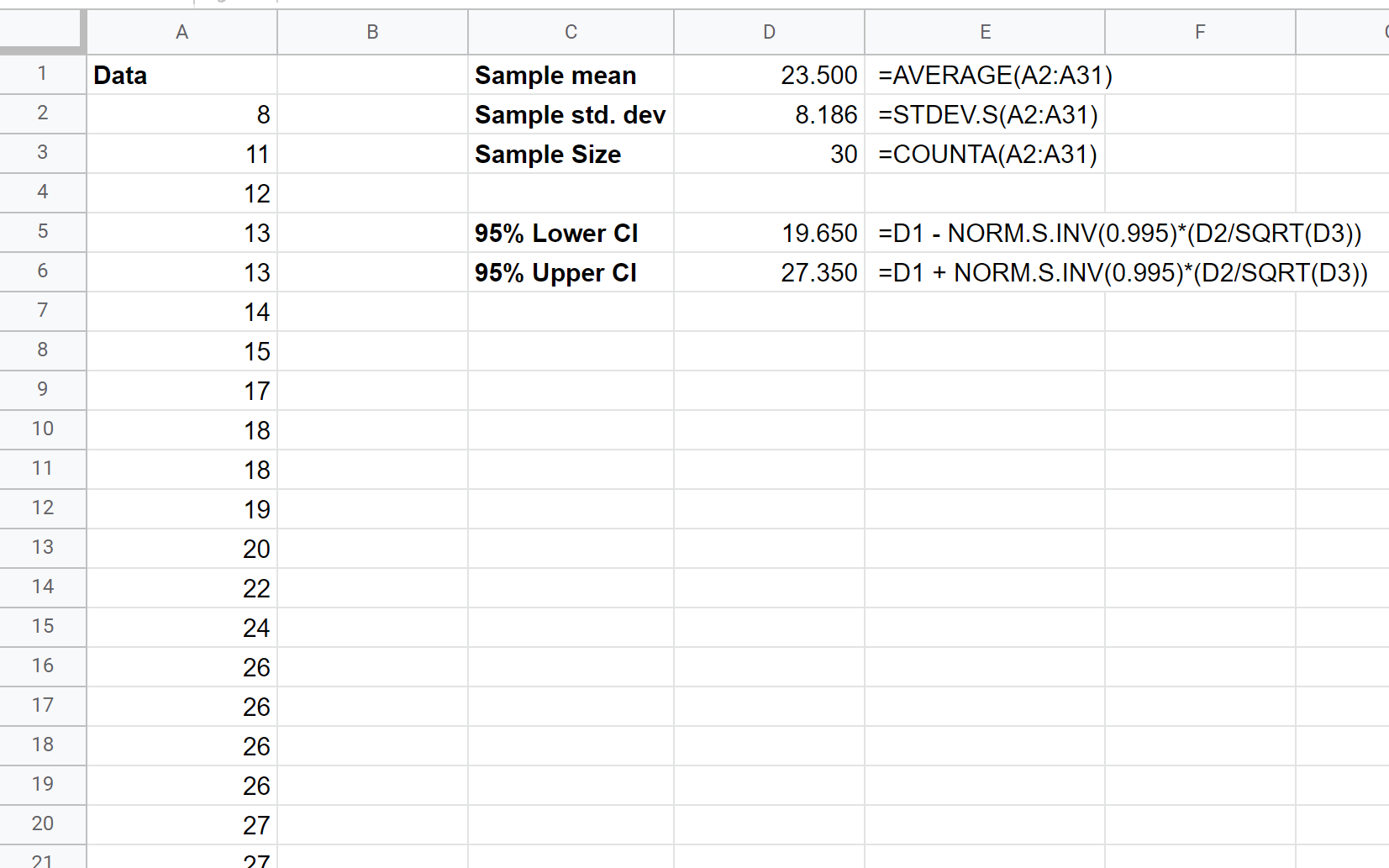
Das 99 %-Konfidenzintervall für die tatsächliche mittlere Bevölkerungsgröße beträgt (19,650, 27,350) .

Beachten Sie, dass dieses 99 %-Konfidenzintervall breiter ist als das zuvor berechnete 95 %-Konfidenzintervall.

Verwandt: Konfidenzniveau vs. Konfidenzintervall: Was ist der Unterschied?

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie man Konfidenzintervalle mit anderer Statistiksoftware berechnet:

So berechnen Sie Konfidenzintervalle in Excel
So berechnen Sie Konfidenzintervalle in R
So berechnen Sie Konfidenzintervalle in Python