So berechnen sie konfidenzintervalle in excel
EinKonfidenzintervall ist ein Wertebereich, der wahrscheinlich einen Populationsparameter mit einem bestimmten Konfidenzniveau enthält. Die Berechnung erfolgt nach folgender allgemeiner Formel:
Konfidenzintervall = (Punktschätzung) +/- (kritischer Wert)* (Standardfehler)
Diese Formel erstellt ein Intervall mit einer Untergrenze und einer Obergrenze, das wahrscheinlich einen Populationsparameter mit einem gewissen Maß an Konfidenz enthält:
Konfidenzintervall = [untere Grenze, obere Grenze]
In diesem Tutorial wird erläutert, wie Sie die folgenden Konfidenzintervalle in Excel berechnen:
1. Konfidenzintervall für einen Mittelwert
2. Konfidenzintervall für einen Mittelwertunterschied
3. Konfidenzintervall für einen Anteil
4. Konfidenzintervall für einen Unterschied in den Proportionen
Lass uns gehen!
Beispiel 1: Konfidenzintervall für einen Mittelwert
Wir verwenden die folgende Formel, um ein Konfidenzintervall für einen Mittelwert zu berechnen:
Konfidenzintervall = x +/- z*(s/√n)
Gold:
- x : Stichprobenmittel
- z: der gewählte z-Wert
- s: Stichprobenstandardabweichung
- n: Stichprobengröße
Beispiel: Angenommen, wir sammeln eine Zufallsstichprobe von Schildkröten mit den folgenden Informationen:
- Stichprobengröße n = 25
- Durchschnittliches Probengewicht x = 300
- Stichprobenstandardabweichung s = 18,5
Der folgende Screenshot zeigt, wie ein 95 %-Konfidenzintervall für das tatsächliche Durchschnittsgewicht der Schildkrötenpopulation berechnet wird:
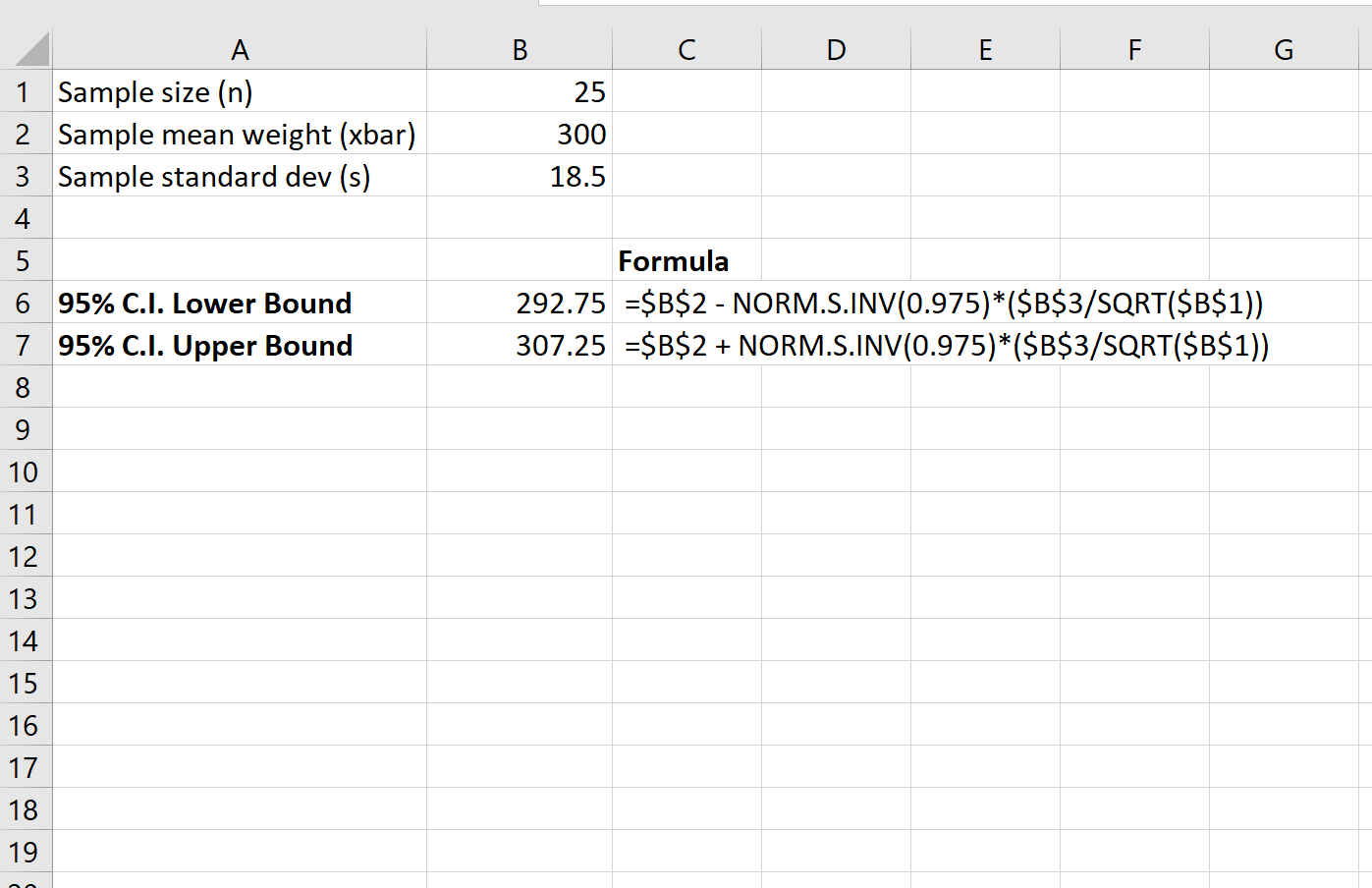
Das 95 %-Konfidenzintervall für das tatsächliche mittlere Gewicht der Schildkrötenpopulation beträgt [292,75, 307,25] .
Beispiel 2: Konfidenzintervall für eine Mittelwertdifferenz
Wir verwenden die folgende Formel, um ein Konfidenzintervall für einen Unterschied in den Mittelwerten der Grundgesamtheit zu berechnen:
Konfidenzintervall = ( x 1 – x 2 ) +/- t*√((s p 2 /n 1 ) + (s p 2 /n 2 ))
Gold:
- x 1 , x 2 : Mittelwert von Stichprobe 1, Mittelwert von Stichprobe 2
- t: der t-kritische Wert basierend auf dem Konfidenzniveau und den Freiheitsgraden (n 1 + n 2 -2).
- s p 2 : gepoolte Varianz, berechnet als ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- t: der t-kritische Wert
- n 1 , n 2 : Stichprobengröße 1, Stichprobengröße 2
Beispiel: Angenommen, wir möchten den Unterschied im Durchschnittsgewicht zwischen zwei verschiedenen Schildkrötenarten schätzen. Wir sammeln daher eine Zufallsstichprobe von 15 Schildkröten aus jeder Population. Hier sind die zusammenfassenden Daten für jede Probe:
Probe 1:
- x1 = 310
- s 1 = 18,5
- n 1 = 15
Probe 2:
- x2 = 300
- s2 = 16,4
- n2 = 15
Der folgende Screenshot zeigt, wie ein 95 %-Konfidenzintervall für den wahren Unterschied in den Mittelwerten der Grundgesamtheit berechnet wird:
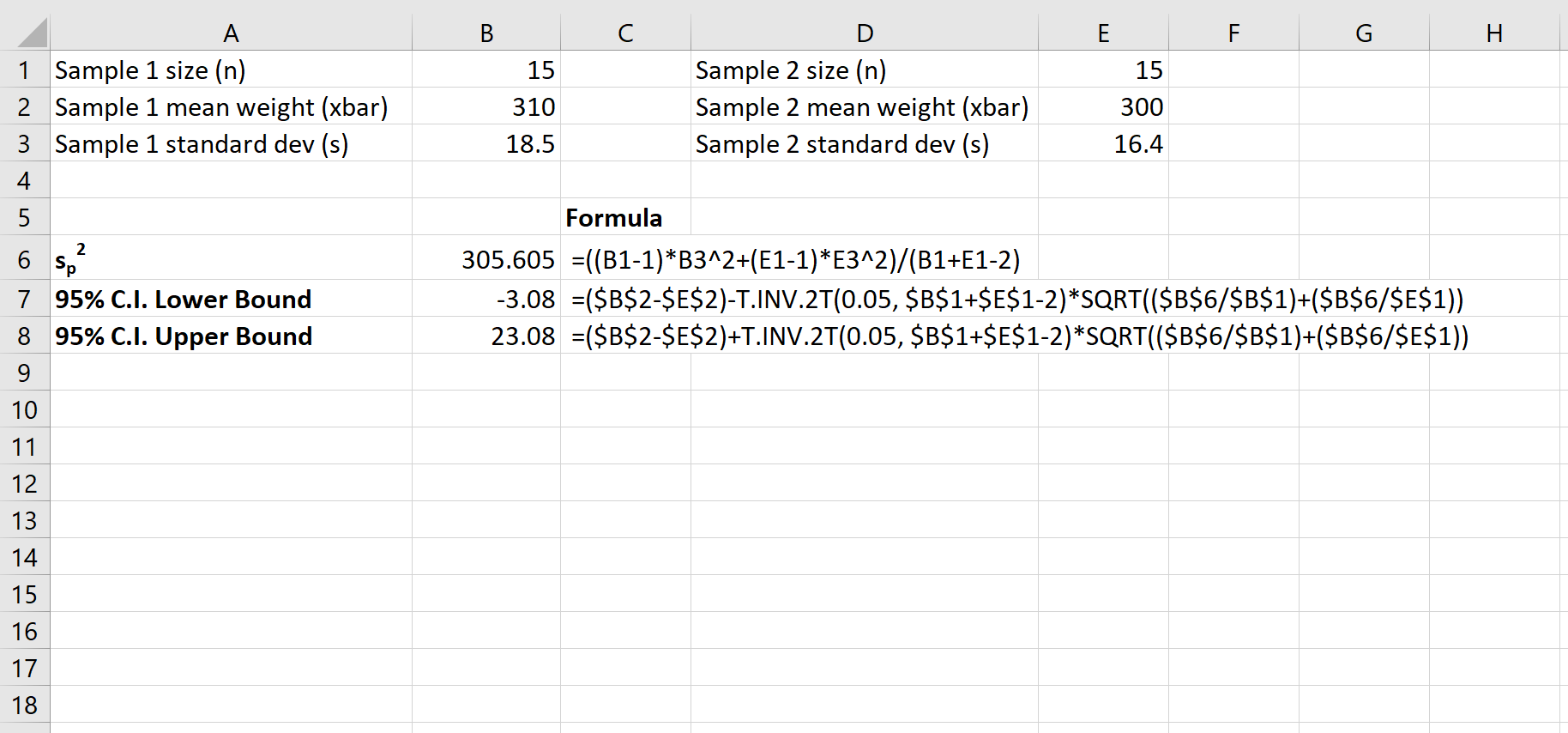
Das 95 %-Konfidenzintervall für die wahre Differenz zwischen den Grundgesamtheitsmittelwerten beträgt [-3,08, 23,08] .
Beispiel 3: Konfidenzintervall für einen Anteil
Wir verwenden die folgende Formel, um ein Konfidenzintervall für einen Anteil zu berechnen:
Konfidenzintervall = p +/- z*√ p(1-p) / n
Gold:
- p: Stichprobenanteil
- z: der gewählte z-Wert
- n: Stichprobengröße
Beispiel: Angenommen, wir möchten den Anteil der Einwohner eines Landkreises schätzen, die ein bestimmtes Gesetz befürworten. Wir wählen eine Zufallsstichprobe von 100 Einwohnern aus und fragen sie, wie sie zum Gesetz stehen. Hier sind die Ergebnisse:
- Stichprobengröße n = 100
- Anteil der Befürworter des Gesetzes p = 0,56
Der folgende Screenshot zeigt, wie ein 95 %-Konfidenzintervall für den tatsächlichen Anteil der landesweiten Einwohner berechnet wird, die das Gesetz befürworten:
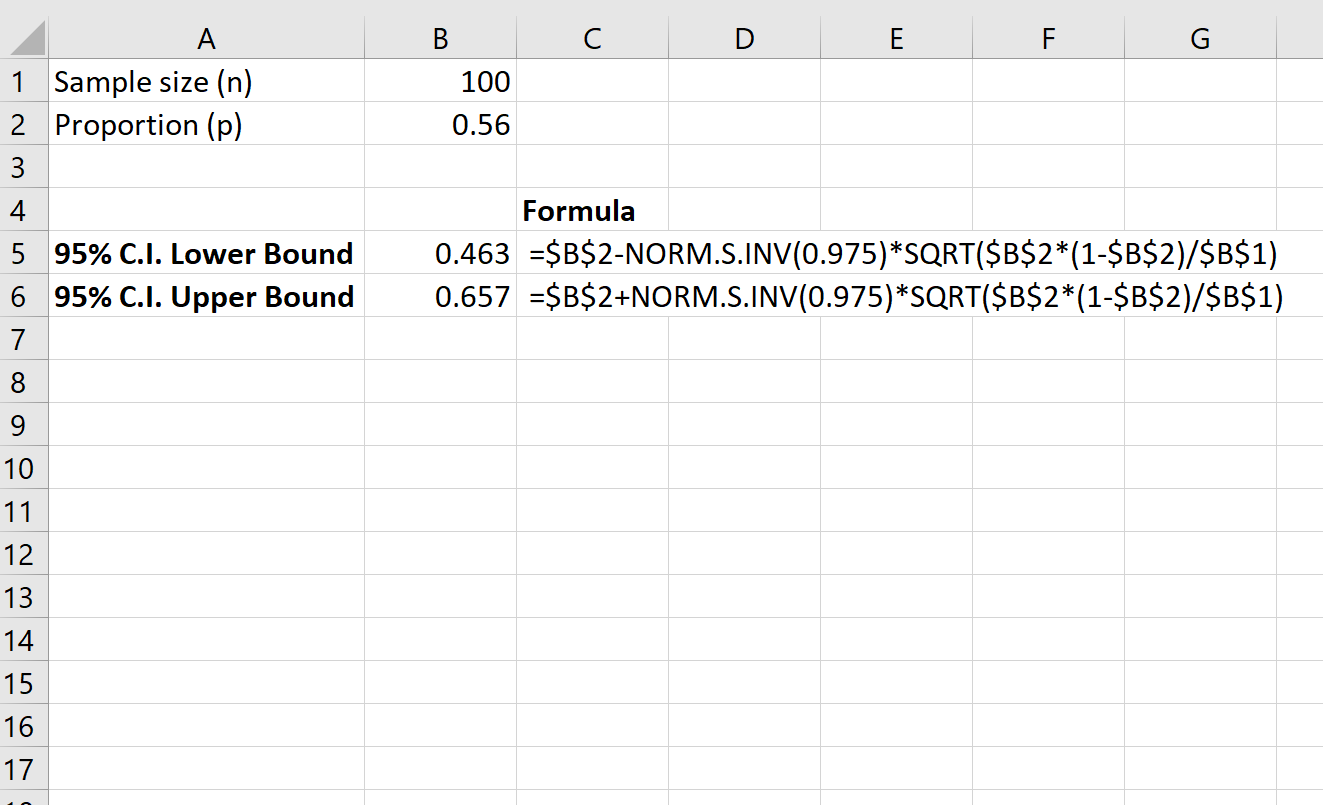
Das 95 %-Konfidenzintervall für den tatsächlichen Anteil der Einwohner im gesamten Landkreis, die das Gesetz befürworten, beträgt [.463, .657] .
Beispiel 4: Konfidenzintervall für einen Unterschied in den Proportionen
Wir verwenden die folgende Formel, um ein Konfidenzintervall für einen Unterschied in den Proportionen zu berechnen:
Konfidenzintervall = (p 1 – p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Gold:
- p 1 , p 2 : Anteil von Probe 1, Anteil von Probe 2
- z: der z-kritische Wert basierend auf dem Konfidenzniveau
- n 1 , n 2 : Stichprobengröße 1, Stichprobengröße 2
Beispiel: Angenommen, wir möchten den Unterschied zwischen dem Anteil der Einwohner, die ein bestimmtes Gesetz in Landkreis A unterstützen, und dem Anteil, der das Gesetz in Landkreis B unterstützt, schätzen. Hier sind die zusammenfassenden Daten für jede Stichprobe:
Probe 1:
- n 1 = 100
- p 1 = 0,62 (d. h. 62 von 100 Einwohnern unterstützen das Gesetz)
Probe 2:
- n2 = 100
- p 2 = 0,46 (d. h. 46 von 100 Einwohnern unterstützen das Gesetz)
Der folgende Screenshot zeigt, wie ein 95 %-Konfidenzintervall für den tatsächlichen Unterschied im Anteil der Einwohner, die das Gesetz unterstützen, zwischen den Landkreisen berechnet wird:
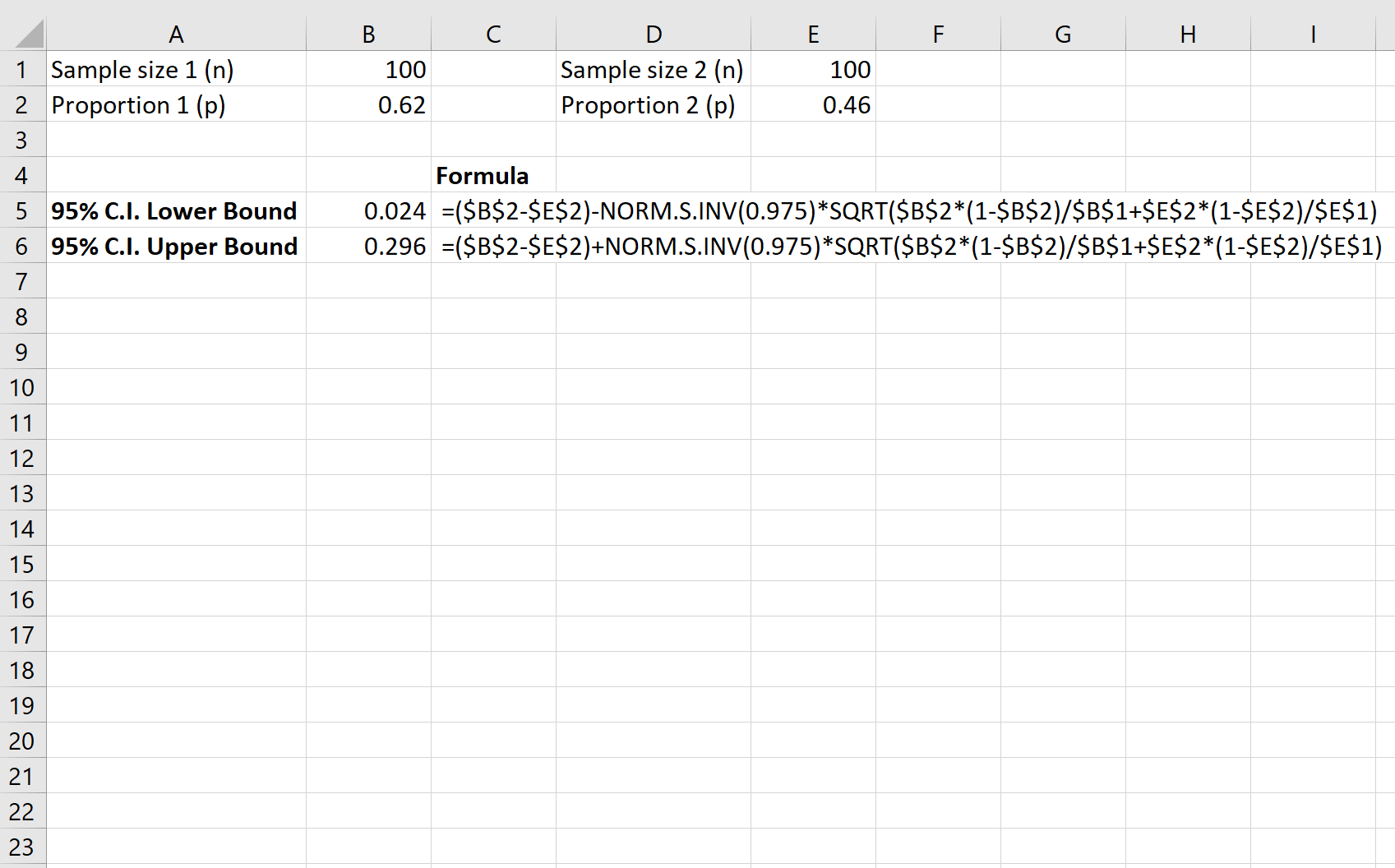
Das 9,5 %-Konfidenzintervall für den tatsächlichen Unterschied im Anteil der Einwohner, die das Gesetz zwischen den Landkreisen unterstützen, beträgt [0,024, 0,296] .
Weitere Excel-Tutorials finden Sie hier .
Über den Autor
Dr. Benjamin Anderson
Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen