Eine einfache erklärung der kontinuitätskorrektur in der statistik
Die Kontinuitätskorrektur wird angewendet, wenn Sie eine kontinuierliche Verteilung verwenden möchten, um eine diskrete Verteilung anzunähern. Im Allgemeinen wird es verwendet, wenn Sie eine Normalverteilung verwenden möchten, um eine Binomialverteilung anzunähern.
Denken Sie daran, dass die Binomialverteilung uns die Wahrscheinlichkeit angibt, in n Versuchen x Erfolg zu erzielen, vorausgesetzt, dass die Erfolgswahrscheinlichkeit in einem einzelnen Versuch p beträgt. Um Fragen zur Wahrscheinlichkeit mit einer Binomialverteilung zu beantworten, könnten wir einfach einen Binomialverteilungsrechner verwenden, wir könnten die Wahrscheinlichkeit aber auch mithilfe einer Normalverteilung mit einer Kontinuitätskorrektur annähern .
Als Kontinuitätskorrektur bezeichnet man das Addieren oder Subtrahieren von 0,5 von einem diskreten x-Wert .
Nehmen wir zum Beispiel an, wir möchten die Wahrscheinlichkeit ermitteln, dass eine Münze im Laufe von 100 Würfen höchstens 45 Mal auf dem Kopf landet. Das heißt, wir wollen P(X ≤ 45) finden. Um die Normalverteilung zur Annäherung an die Binomialverteilung zu verwenden, würden wir stattdessen P(X ≤ 45,5) finden.
Die folgende Tabelle zeigt, wann Sie 0,5 addieren oder subtrahieren sollten, abhängig von der Art der Wahrscheinlichkeit, die Sie ermitteln möchten:
| Verwenden Sie die Binomialverteilung | Verwendung der Normalverteilung mit Kontinuitätskorrektur |
|---|---|
| X = 45 | 44,5 < X < 45,5 |
| X ≤ 45 | X < 45,5 |
| X < 45 | X < 44,5 |
| X ≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Notiz:
Es ist nur dann sinnvoll, eine Kontinuitätskorrektur auf die Normalverteilung anzuwenden, um die Binomialverteilung anzunähern, wenn n*p und n*(1-p) beide mindestens 5 sind.
Angenommen, n = 15 und p = 0,6. In diesem Fall:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Da beide Zahlen größer oder gleich 5 sind, wäre es akzeptabel, in diesem Szenario eine Kontinuitätskorrektur anzuwenden.
Das folgende Beispiel veranschaulicht, wie eine Kontinuitätskorrektur auf die Normalverteilung angewendet wird, um die Binomialverteilung anzunähern.
Beispiel für die Anwendung der Kontinuitätskorrektur
Angenommen, wir möchten wissen, wie wahrscheinlich es ist, dass eine Münze in 100 Würfen höchstens 43 Mal auf „Kopf“ landet. In diesem Fall:
n = Anzahl der Versuche = 100
X = Anzahl der Erfolge = 43
p = Erfolgswahrscheinlichkeit in einem bestimmten Versuch = 0,50
Wir können diese Zahlen in den Binomialverteilungsrechner eingeben, um zu sehen, dass die Wahrscheinlichkeit, dass die Münze weniger als oder gleich 43 Mal auf „Kopf“ landet, 0,09667 beträgt.
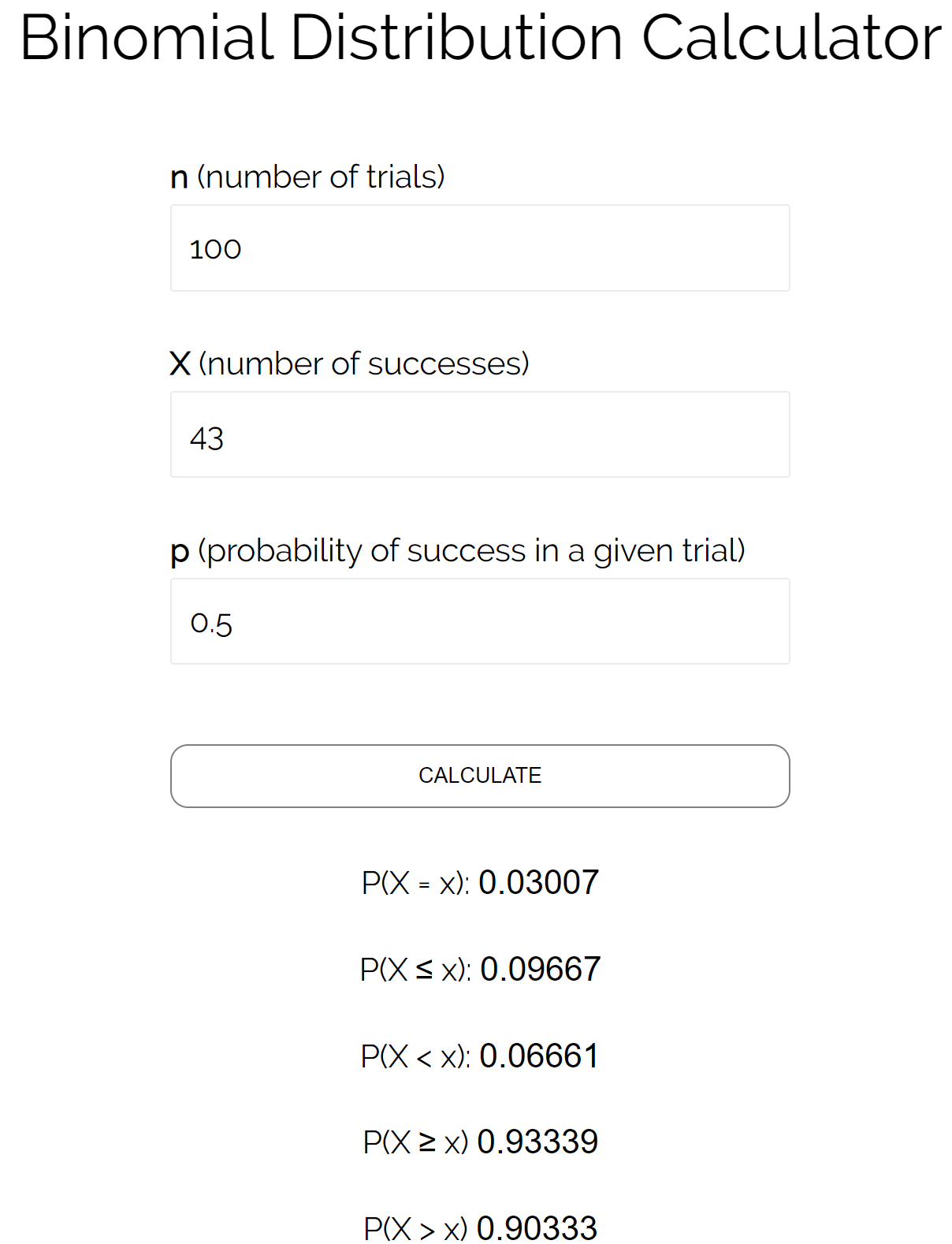
Um die Binomialverteilung durch Anwenden einer Kontinuitätskorrektur auf die Normalverteilung anzunähern, können wir die folgenden Schritte verwenden:
Schritt 1: Stellen Sie sicher, dass n*p und n*(1-p) beide mindestens 5 sind .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Beide Zahlen sind größer oder gleich 5, also können wir fortfahren.
Schritt 2: Bestimmen Sie, ob 0,5 addiert oder subtrahiert werden soll
Anhand der obigen Tabelle sehen wir, dass wir 0,5 hinzufügen müssen, wenn wir mit der Wahrscheinlichkeit in der Form X ≤ 43 arbeiten. Somit finden wir P(X< 43,5).
Schritt 3: Ermitteln Sie den Mittelwert (μ) und die Standardabweichung (σ) der Binomialverteilung.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
Schritt 4: Ermitteln Sie den Z-Score anhand des im vorherigen Schritt ermittelten Mittelwerts und der Standardabweichung.
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
Schritt 5: Verwenden Sie die Z-Tabelle, um die mit dem Z-Score verbundene Wahrscheinlichkeit zu ermitteln.
Gemäß Tabelle Z beträgt die mit z = -1,3 verbundene Wahrscheinlichkeit 0,0968 .
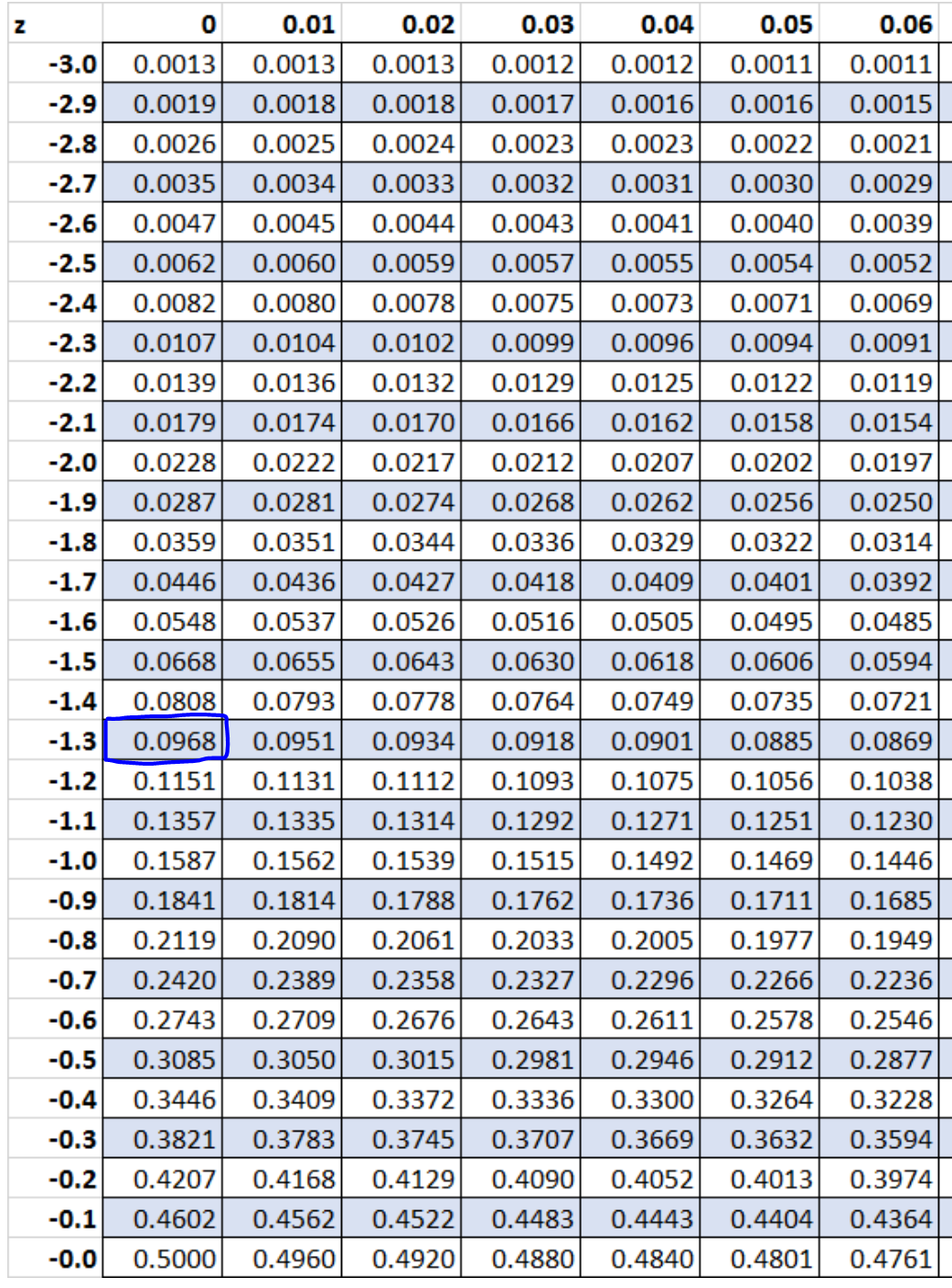
Die genaue Wahrscheinlichkeit, die wir mithilfe der Binomialverteilung ermittelt haben, betrug also 0,09667 , während die ungefähre Wahrscheinlichkeit, die wir anhand der Kontinuitätskorrektur mit der Normalverteilung ermittelt haben, 0,0968 betrug. Diese beiden Werte sind ziemlich geschlossen.
Wann sollte die Kontinuitätskorrektur verwendet werden?
Bevor es moderne Statistiksoftware gab und Berechnungen manuell durchgeführt werden mussten, wurden Kontinuitätskorrekturen häufig verwendet, um Wahrscheinlichkeiten mit diskreten Verteilungen zu ermitteln. Heutzutage spielen Kontinuitätskorrekturen bei der Berechnung von Wahrscheinlichkeiten weniger eine Rolle, da wir uns normalerweise auf Software oder Taschenrechner verlassen können, um Wahrscheinlichkeiten für uns zu berechnen.
Stattdessen handelt es sich lediglich um ein Thema, das in Statistikkursen behandelt wird, um die Beziehung zwischen einer Binomialverteilung und einer Normalverteilung zu veranschaulichen und zu zeigen, dass es für eine Normalverteilung möglich ist, sich einer Binomialverteilung anzunähern, indem eine Kontinuitätskorrektur angewendet wird.
Kontinuitätskorrekturrechner
Verwenden Sie den Kontinuitätskorrekturrechner , um automatisch eine Kontinuitätskorrektur auf eine Normalverteilung anzuwenden, um Binomialwahrscheinlichkeiten anzunähern.