Kontrollgrenzen

Von Dr. Benjamin Anderson August 2, 2023 Qualitätsmanagement Keine Kommentare

In diesem Artikel wird erläutert, was eine Kontrollgrenze ist und welche verschiedenen Kontrollgrenzen eine Kontrollkarte aufweist. Außerdem sehen Sie, wie Eingriffsgrenzen berechnet werden, sowie ein ausgearbeitetes Beispiel, in dem die Eingriffsgrenzen eines Prozesses ermittelt werden.

Was sind Kontrollgrenzen?

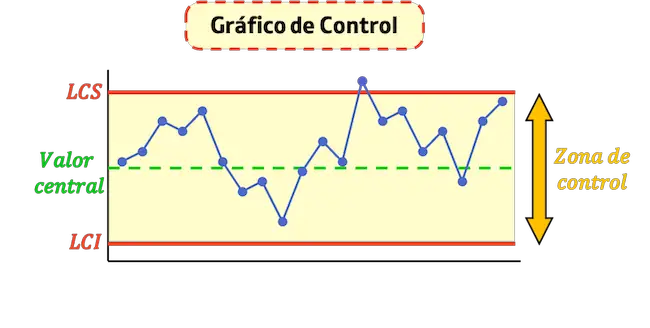
Kontrollgrenzen sind die horizontalen Linien auf einem Kontrolldiagramm, die zur Bestimmung dienen, ob ein Prozess kontrolliert wird oder nicht.

Eine Kontrollkarte hat zwei Kontrollgrenzen: die obere und die untere Kontrollgrenze, die den Kontrollbereich oben bzw. unten abgrenzen.

Kontrollgrenzen sind also Werte, die den Kontrollbereich eines Prozesses angeben. Wenn die von einem Prozess erhaltene Messung innerhalb der Kontrollgrenzen liegt, bedeutet dies, dass der Prozess kontrolliert wird. Andernfalls muss die Maschine oder der Prozess überprüft werden, da eine Abweichung wahrscheinlich ist.

Arten von Kontrollgrenzen

Die Kontrollgrenzen sind:

Obere Kontrollgrenze (LCS) : Dies ist die Linie, die den im Prozess akzeptierten Maximalwert angibt.
Untere Kontrollgrenze (LCI) : Dies ist die Linie, die den im Prozess akzeptierten Mindestwert angibt.
Zentrale Kontrolllinie : Dies ist die Linie, die den Durchschnittswert des Diagramms darstellt. Je näher die Punkte an dieser Linie liegen, desto stabiler ist der Prozess.

So berechnen Sie Kontrollgrenzen

Derzeit werden die Kontrollgrenzen eines Prozesses im Allgemeinen durch Computersoftware berechnet, die eine Steuerung des Prozesses ermöglicht. Es ist jedoch auch wichtig, dass Sie wissen, wie sie berechnet werden, da Sie sie möglicherweise manuell ermitteln müssen.

Die Berechnung der Kontrollgrenzen einer Kontrollkarte hängt von der Art der Karte ab, die Sie erstellen möchten, da sich die Werte ändern, je nachdem, ob es sich um eine Kontrollkarte für den Mittelwert oder für den Bereich handelt.

Das Durchschnittskontrolldiagramm ist ein Diagramm, in dem die Entwicklung des Durchschnitts eines Prozesses ausgewertet wird. Der Durchschnitt einer Reihe von Werten wird also nach der folgenden Formel berechnet:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Gold:

$x_i$

ist die Maßzahl i.
$n$

ist die Anzahl der durchgeführten Messungen.

Den zentralen Wert der Kontrollkarte für den Mittelwert bezeichnen wir als

$\overline{\overline{X}}$

, der der Durchschnitt der Stichproben ist und mit dem folgenden Ausdruck berechnet wird:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Gold:

$\overline{X}_j$

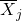
ist der Mittelwert der Stichprobe j.
$m$

ist die Anzahl der entnommenen Proben.

➤ Siehe: Berechnung des arithmetischen Mittels

Im Gegensatz dazu ist der zentrale Wert der Ausdehnungskontrollkarte der Durchschnitt der Ausdehnungen aller entnommenen Proben:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Gold:

$R_j$

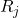
ist der Bereich der Probe j.
$m$

ist die Anzahl der entnommenen Proben.

➤ Siehe: Berechnung der statistischen Reichweite

Daher lauten die Formeln zur Berechnung der Kontrollgrenzen einer Kontrollkarte wie folgt:

Steuerkarte

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

R-Steuerkarte

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Wobei die Werte der Parameter A ₂ , D ₃ und D ₄ in der folgenden Tabelle zu finden sind:

Größe (Nr.)	Um ₂	Tag ₃	_D4
2	1.880	0,000	3.267
3	1.023	0,000	2.575
4	0,729	0,000	2.282
5	0,577	0,000	2.115
6	0,483	0,000	2004
7	0,419	0,076	1.924
8	0,373	0,136	1.864
9	0,337	0,184	1.816
zehn	0,308	0,223	1.777

Beispiel für die Berechnung von Kontrollgrenzen

Ein Industrieunternehmen möchte die Messung des Durchmessers eines Zylinders kontrollieren, um zu sehen, ob sein Produktionsprozess unter Kontrolle ist. Nehmen Sie dazu alle 15 Minuten eine Probe von 5 Zylindern und messen Sie deren Durchmesser. Die folgende Tabelle zeigt die Messaufzeichnung.

Um die Kontrollgrenzen zu ermitteln, müssen wir zunächst das arithmetische Mittel und den Bereich jeder Messreihe ermitteln:

Berechnen wir nun den Durchschnitt der Mittelwerte und Bereiche, die die zentralen Werte des Kontrolldiagramms für den Durchschnitt bzw. für den Bereich darstellen:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

In diesem Fall besteht jede Probe aus 5 Messungen, die Koeffizienten der Kontrollgrenzenformeln lauten daher wie folgt:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Wir berechnen die oberen und unteren Kontrollgrenzen der durchschnittlichen und erweiterten Kontrollkarte:

Kontrollgrenzen der Kontrollkarte

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Kontrollgrenzen von R-Steuerkarte

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

Die Übungskontrollkarten lauten daher wie folgt:

Beispiel für die Berechnung von Kontrollgrenzen

Im ersten Kontrolldiagramm können wir sehen, dass zwei Werte unter der unteren Kontrollgrenze liegen. Darüber hinaus gibt es in der zweiten Kontrollkarte auch einen Wert oberhalb der oberen Kontrollgrenze. Der Prozess wird daher nicht kontrolliert.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Was sind Kontrollgrenzen?

Arten von Kontrollgrenzen

So berechnen Sie Kontrollgrenzen

Beispiel für die Berechnung von Kontrollgrenzen

Über den Autor

Dr. Benjamin Anderson

Einen Kommentar hinzufügen