Korrelation bedeutet keine kausalität: 5 konkrete beispiele

Der Ausdruck „ Korrelation impliziert keine Kausalität “ wird in der Statistik häufig verwendet, um zu betonen, dass die Korrelation zwischen zwei Variablen nicht unbedingt bedeutet, dass eine Variable die andere verursacht.

Um diesen Ausdruck besser zu verstehen, betrachten Sie die folgenden konkreten Beispiele.

Beispiel 1: Eisverkauf und Hai-Angriffe

Wenn wir jedes Jahr Daten zu den monatlichen Eisverkäufen und den monatlichen Hai-Angriffen in den Vereinigten Staaten sammeln würden, würden wir feststellen, dass die beiden Variablen stark korrelieren.

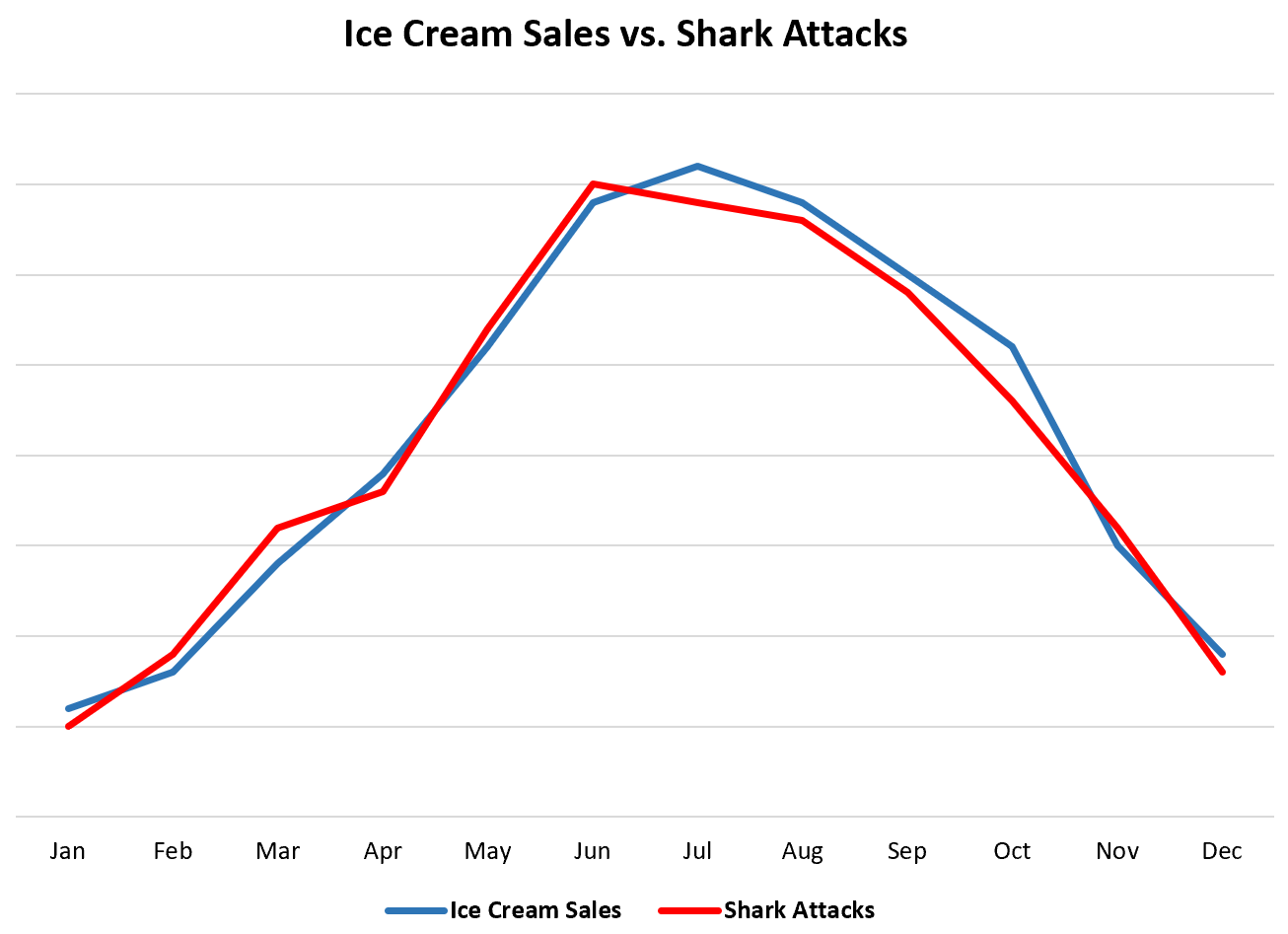
Bedeutet das, dass der Verzehr von Eis zu Hai-Angriffen führt?

Nicht genug. Die wahrscheinlichste Erklärung ist, dass mehr Menschen Eis essen und im Meer schwimmen, wenn es draußen wärmer ist, was erklärt, warum diese beiden Variablen so stark korrelieren.

Obwohl Eisverkäufe und Hai-Angriffe stark miteinander korrelieren, verursacht das eine nicht das andere.

Beispiel 2: Meisterschaften und Einnahmen an den Kinokassen

Wenn wir Daten über die Gesamtzahl der jedes Jahr von Universitäten vergebenen Masterabschlüsse und die pro Jahr erzielten Gesamteinnahmen an den Kinokassen sammeln, würden wir feststellen, dass die beiden Variablen stark korrelieren.

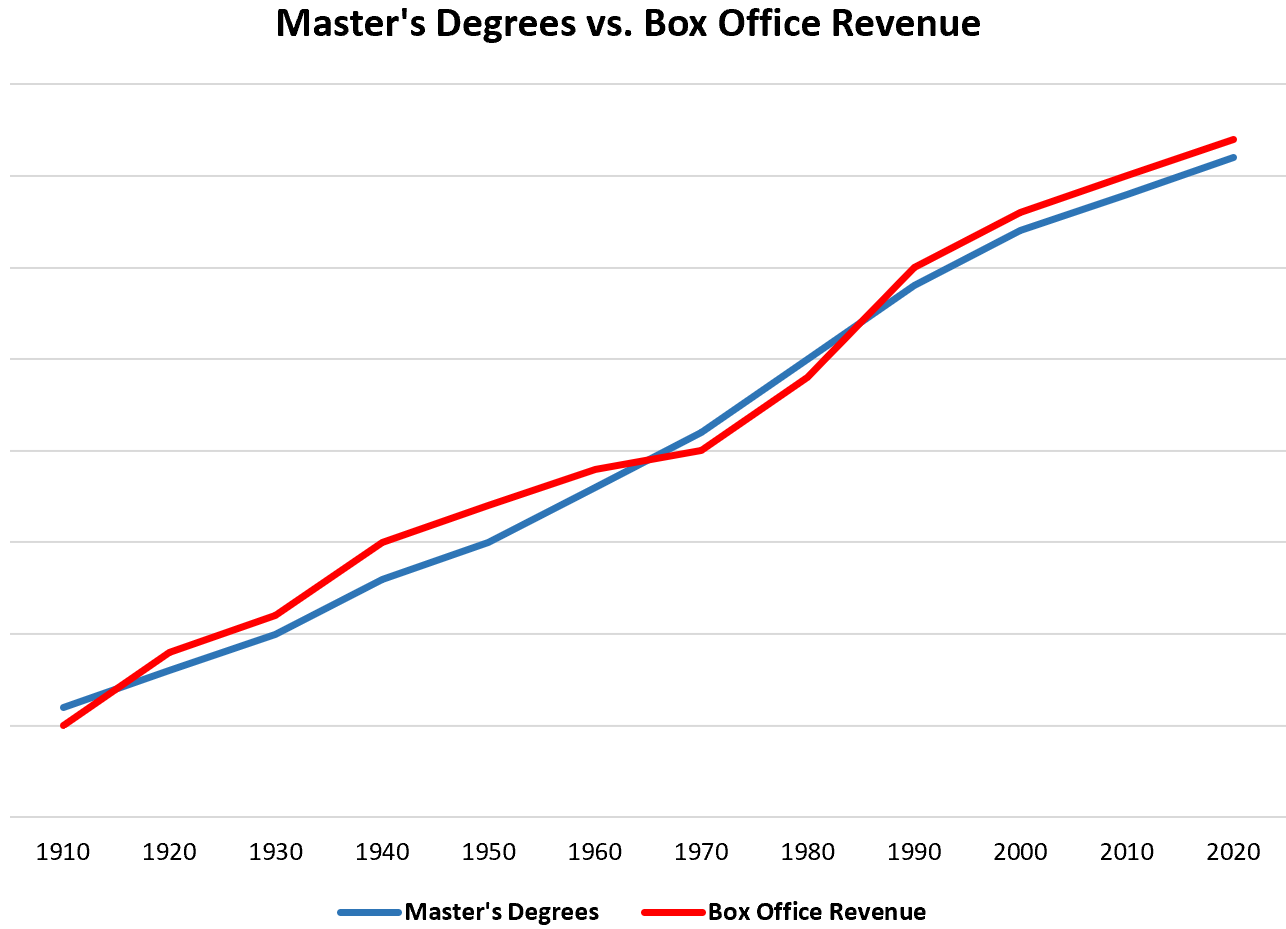
Bedeutet das, dass die Vergabe weiterer Master-Abschlüsse jedes Jahr zu einer Steigerung der Einnahmen an den Kinokassen führt?

Nicht genug. Die wahrscheinlichste Erklärung ist, dass die Weltbevölkerung jedes Jahr wächst, was bedeutet, dass jedes Jahr mehr Master-Abschlüsse verliehen werden und die Zahl der Menschen, die jedes Jahr ins Kino gehen, in etwa im gleichen Verhältnis zunimmt.

Obwohl diese beiden Variablen korrelieren, verursacht die eine die andere nicht.

Beispiel 3: Ertrinkungen in Schwimmbädern im Zusammenhang mit der Kernenergieerzeugung

Wenn wir Daten über die Gesamtzahl der Schwimmbeckenüberflutungen pro Jahr und die Gesamtenergiemenge, die jedes Jahr von Kernkraftwerken erzeugt wird, sammeln würden, würden wir feststellen, dass die beiden Variablen stark korrelieren.

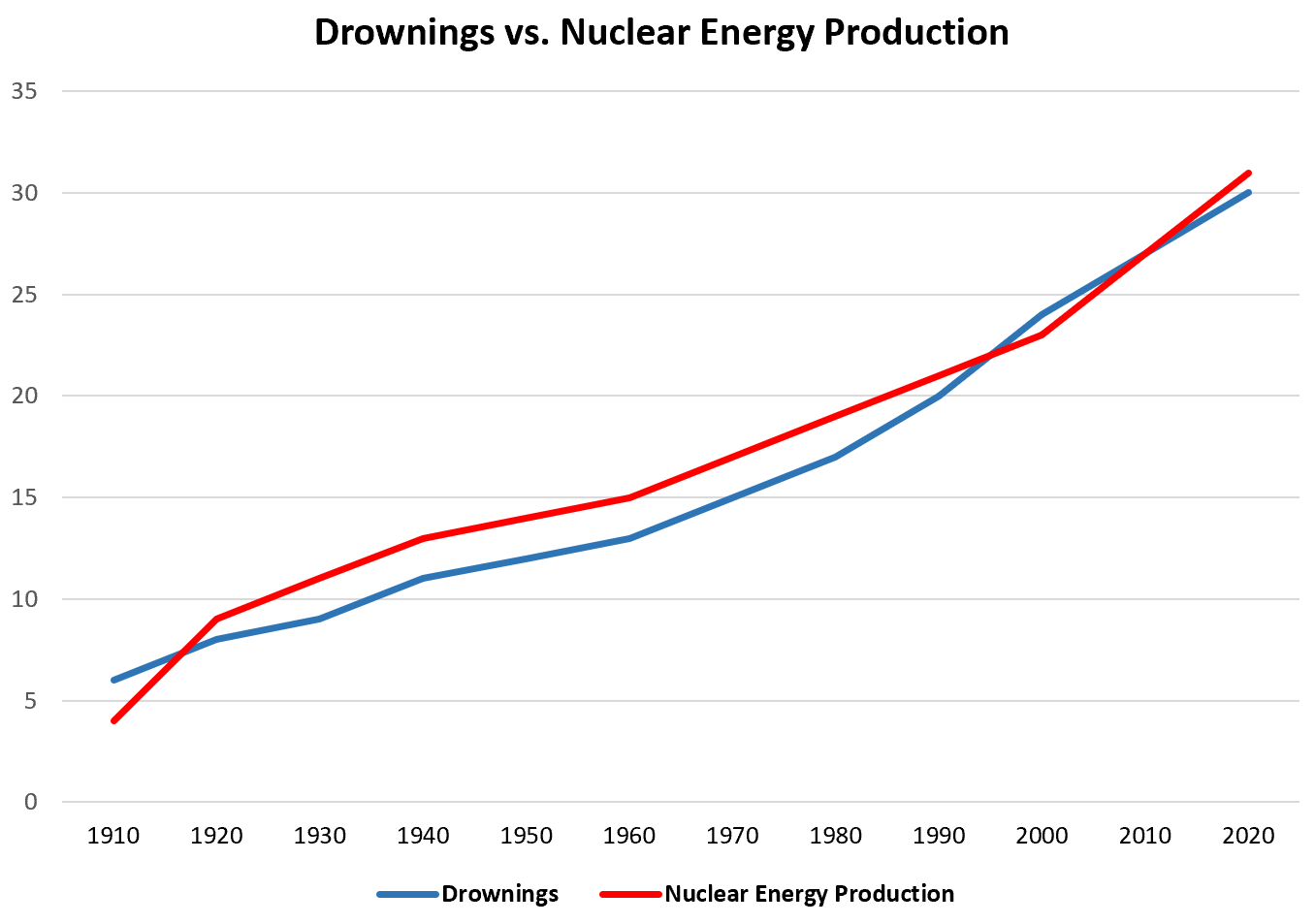
Bedeutet das, dass vermehrtes Ertrinken in Schwimmbädern irgendwie zu einer erhöhten Atomstromproduktion führt?

Nicht genau. Die wahrscheinlichste Erklärung ist, dass die Weltbevölkerung gewachsen ist, was bedeutet, dass immer mehr Menschen in Schwimmbädern ertrinken, und dass die Kernenergieerzeugung von Jahr zu Jahr rentabler wird, weshalb sie zugenommen hat.

Obwohl diese beiden Variablen stark korrelieren, verursacht die eine die andere nicht.

Beispiel 4: Masernfälle im Verhältnis zur Heiratsrate

Wenn wir jedes Jahr Daten zur Gesamtzahl der Masernfälle in den Vereinigten Staaten und zur Heiratsrate sammeln würden, würden wir feststellen, dass die beiden Variablen stark korrelieren.

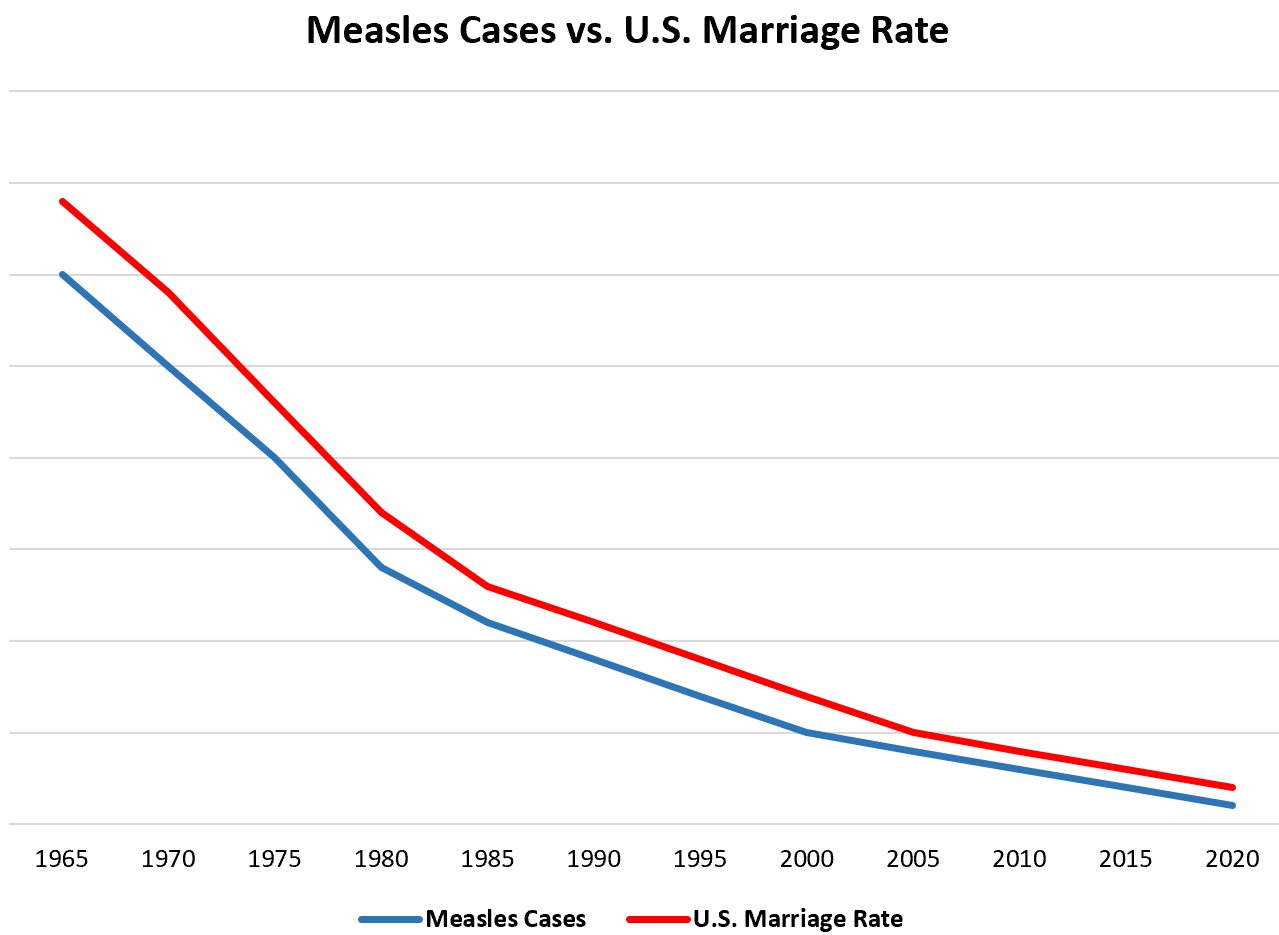
Bedeutet das, dass weniger Masernfälle zu geringeren Heiratsraten führen?

Nicht genau. Stattdessen sind die beiden Variablen unabhängig voneinander: Die moderne Medizin führt zu einem Rückgang der Masernfälle und aus verschiedenen Gründen heiraten jedes Jahr weniger Menschen.

Obwohl diese beiden Variablen stark korrelieren, verursacht die eine die andere nicht.

Beispiel 5: Abiturienten im Verhältnis zum Pizzakonsum

Wenn wir jedes Jahr Daten zur Gesamtzahl der High-School-Absolventen und zum gesamten Pizzakonsum in den Vereinigten Staaten sammeln würden, würden wir feststellen, dass die beiden Variablen stark korrelieren.

Bedeutet dies, dass eine steigende Zahl von High-School-Absolventen zu einem erhöhten Pizzakonsum in den Vereinigten Staaten führt?

Nicht genug. Die wahrscheinlichste Erklärung ist, dass die US-Bevölkerung im Laufe der Zeit gewachsen ist, was bedeutet, dass die Zahl der Menschen mit einem High-School-Abschluss und die Gesamtmenge der konsumierten Pizza mit zunehmender Bevölkerung zunimmt.

Obwohl diese beiden Variablen korrelieren, verursacht die eine die andere nicht.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur Korrelation:

Eine Einführung in den Pearson-Korrelationskoeffizienten
Bedeutet Kausalität Korrelation?
Korrelation vs. Assoziation: Was ist der Unterschied?
Was gilt als „starke“ Korrelation?
Wann sollten Sie Korrelation verwenden?