So berechnen sie die korrelation in sas (mit beispielen)

Eine Möglichkeit, die Beziehung zwischen zwei Variablen zu quantifizieren, ist die Verwendung des Pearson-Korrelationskoeffizienten , der den linearen Zusammenhang zwischen zwei Variablen misst .

Es nimmt immer einen Wert zwischen -1 und 1 an, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Je weiter der Korrelationskoeffizient von Null entfernt ist, desto stärker ist die Beziehung zwischen den beiden Variablen.

Die folgenden Beispiele zeigen, wie proc corr in SAS verwendet wird, um den Korrelationskoeffizienten zwischen Variablen im integrierten SAS-Datensatz „ Fish“ zu berechnen, der verschiedene Messungen für 159 verschiedene Fische enthält, die in einem See in Finnland gefangen wurden.

Wir können proc print verwenden, um die ersten 10 Beobachtungen dieses Datensatzes anzuzeigen:

 /*view first 10 observations from Fish dataset*/
proc print data =sashelp.Fish( obs = 10 );

run ;

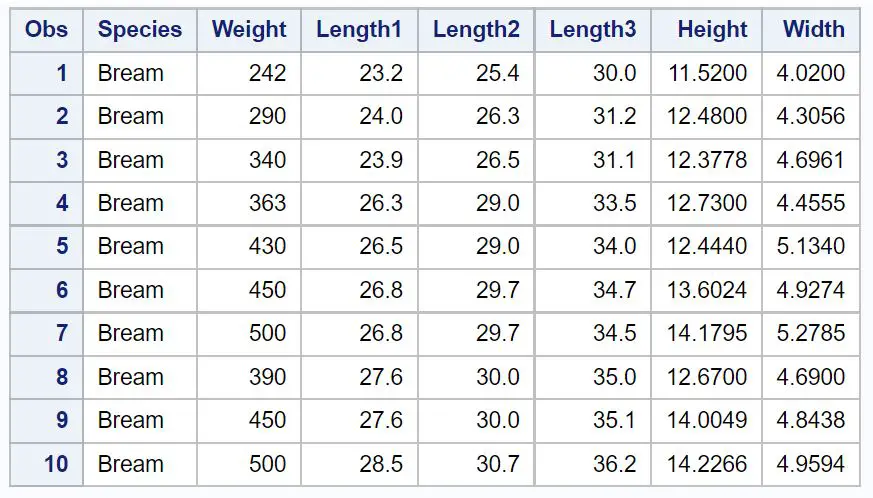
Beispiel 1: Korrelation zwischen zwei Variablen

Wir können den folgenden Code verwenden, um den Pearson-Korrelationskoeffizienten zwischen den Variablen Höhe und Breite zu berechnen:

 /*calculate correlation coefficient between Height and Width*/
proc corr data =sashelp.fish;
	var HeightWidth;

run ;

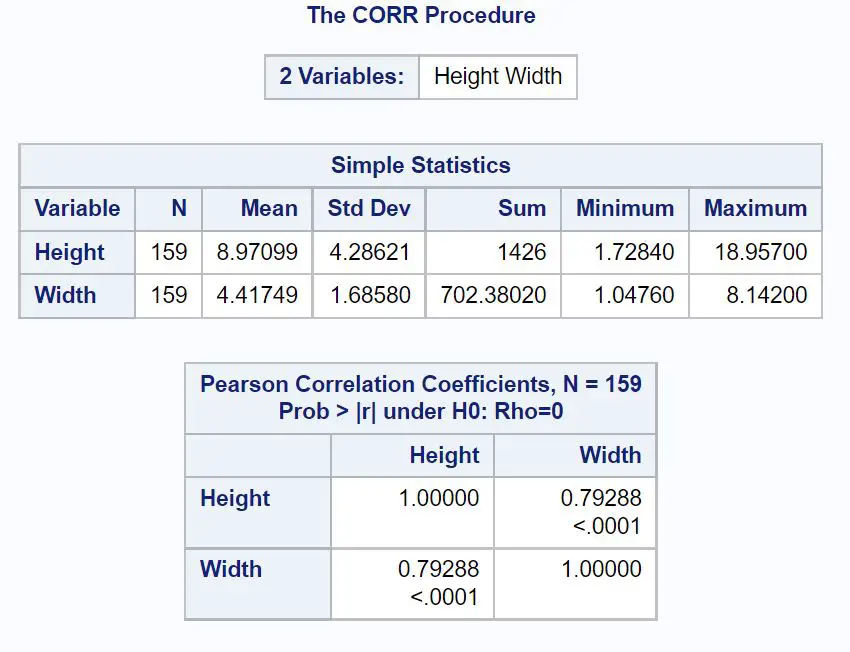
In der ersten Tabelle werden zusammenfassende Statistiken für Höhe und Breite angezeigt.

Die zweite Tabelle zeigt den Pearson-Korrelationskoeffizienten zwischen den beiden Variablen, einschließlich eines p-Werts , der uns sagt, ob die Korrelation statistisch signifikant ist.

Aus dem Ergebnis können wir sehen:

• Pearson-Korrelationskoeffizient: 0,79288
• P-Wert: <0,0001

Dies zeigt uns, dass zwischen Höhe und Breite eine starke positive Korrelation besteht und dass die Korrelation statistisch signifikant ist, da der p-Wert kleiner als α = 0,05 ist.

Verwandt: Was gilt als „starke“ Korrelation?

Beispiel 2: Korrelation zwischen allen Variablen

Mit dem folgenden Code können wir den Pearson-Korrelationskoeffizienten zwischen allen paarweisen Kombinationen von Variablen im Datensatz berechnen:

 /*calculate correlation coefficient between all pairwise combinations of variables*/
proc corr data =sashelp.fish;

run;

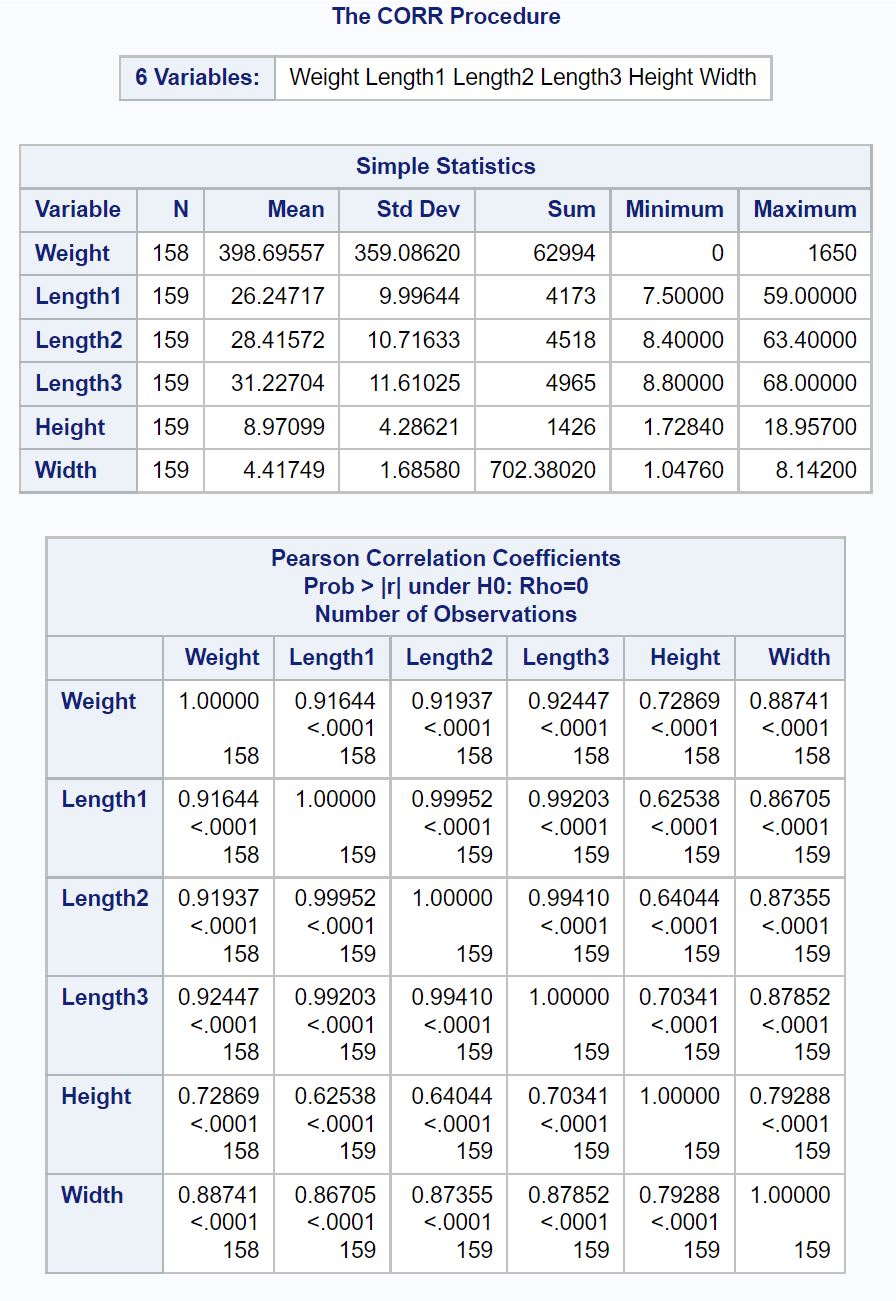
Das Ergebnis zeigt eine Korrelationsmatrix an, die den Pearson-Korrelationskoeffizienten und die entsprechenden p-Werte für jede paarweise Kombination numerischer Variablen im Datensatz enthält.

Zum Beispiel:

• Der Pearson-Korrelationskoeffizient zwischen Gewicht und Länge1 beträgt 0,91644.
• Der Pearson-Korrelationskoeffizient zwischen Gewicht und Länge2 beträgt 0,91937.
• Der Pearson-Korrelationskoeffizient zwischen Gewicht und Länge3 beträgt 0,92447.

Und so weiter.

Beispiel 3: Visualisieren Sie die Korrelation mit einem Streudiagramm

Wir können die Plots- Funktion auch verwenden, um ein Streudiagramm zu erstellen, um die Korrelation zwischen zwei Variablen zu visualisieren:

 /*visualize correlation between Height and Width*/
proc corr data =sashelp.fish plots =scatter( nvar =all);;
	var HeightWidth;

run; 

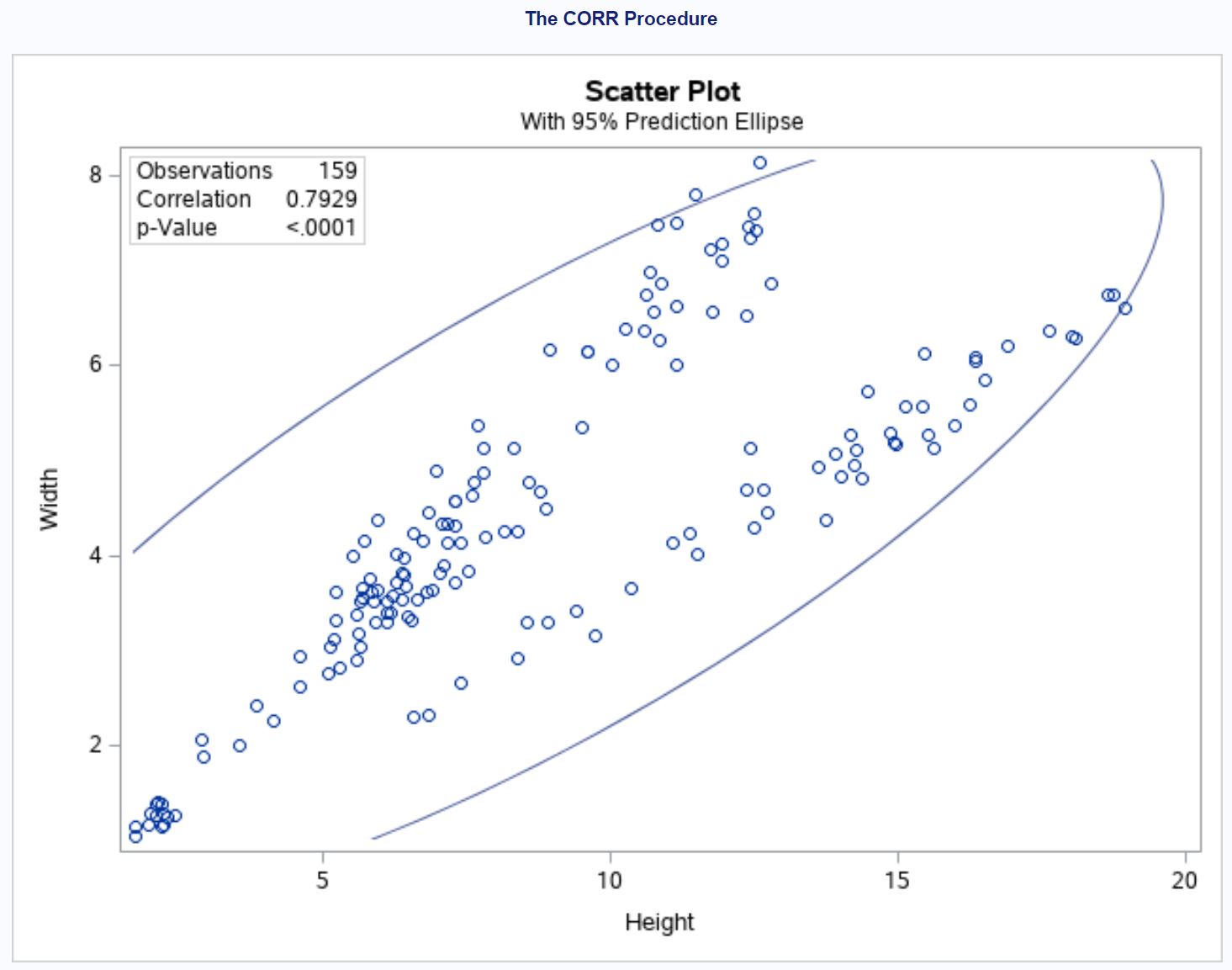
In der Grafik können wir die starke positive Korrelation zwischen Höhe und Breite erkennen. Mit zunehmender Höhe nimmt tendenziell auch die Breite zu.

In der oberen linken Ecke des Diagramms sehen wir außerdem die insgesamt verwendeten Beobachtungen, den Korrelationskoeffizienten und den p-Wert des Korrelationskoeffizienten.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere gängige Vorgänge in SAS ausführen:

So erstellen Sie Häufigkeitstabellen in SAS
So berechnen Sie deskriptive Statistiken in SAS