Was ist korrelation nullter ordnung?

In der Statistik gibt uns die Korrelation zwischen zwei Variablen Auskunft über die Beziehung zwischen diesen beiden Variablen.

Eine der grundlegendsten Korrelationsarten ist die sogenannte Korrelation nullter Ordnung , die sich auf die Korrelation zwischen zwei Variablen bezieht, ohne den möglichen Einfluss anderer Variablen zu berücksichtigen.

Ein Beispiel für diese Art von Korrelation ist der Pearson-Korrelationskoeffizient , der den linearen Zusammenhang zwischen zwei Variablen misst und Werte zwischen -1 und 1 annehmen kann, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Je weiter die Korrelation von Null entfernt ist, desto stärker ist der Zusammenhang zwischen den beiden Variablen.

Korrelationen erster und zweiter Ordnung

Wenn wir die Korrelation zwischen zwei Variablen A und B berechnen und dabei den Einfluss einer dritten Variablen C berücksichtigen, würden wir die Korrelation zwischen A und B als Korrelation erster Ordnung bezeichnen.

Wenn wir in ähnlicher Weise die Korrelation zwischen zwei Variablen A und B berechnen und dabei den Einfluss der Variablen C und D berücksichtigen, würden wir die Korrelation zwischen A und B als Korrelation zweiter Ordnung bezeichnen.

Beispiel einer Korrelation nullter Ordnung

Nehmen wir an, wir haben den folgenden Datensatz, der die Anzahl der Lernstunden und die bei der Prüfung erzielte Note von 10 verschiedenen Studenten zeigt:

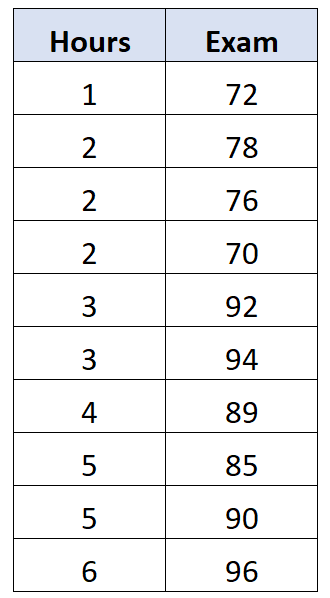
Es stellt sich heraus, dass die Korrelation zwischen diesen beiden Variablen 0,762 beträgt. Dies würde als Korrelation nullter Ordnung zwischen den beiden Variablen angesehen werden, da wir den möglichen Einfluss einer dritten Variablen nicht kontrollieren.

Tatsächlich ist es jedoch möglich, dass andere Faktoren die Beziehung zwischen diesen beiden Variablen beeinflussen.

Beispielsweise kann sich die aktuelle Note des Schülers in der Klasse auf sein Prüfungsergebnis auswirken. Angenommen, wir haben auch Zugriff auf diese Daten:

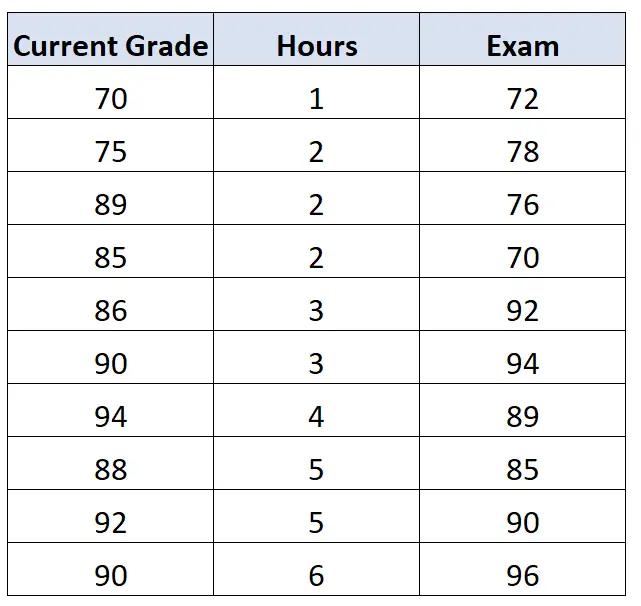
Wenn wir dann die Korrelation zwischen Stunden und Prüfung berechnen und dabei den Einfluss der aktuellen Note berücksichtigen würden , würden wir feststellen, dass die Korrelation erster Ordnung zwischen Stunden und Prüfung 0,578 beträgt.

Dies bedeutet, dass es immer noch eine ziemlich starke positive Korrelation zwischen den gelernten Stunden und der Prüfungsnote gibt, selbst nach Berücksichtigung der Auswirkungen der aktuellen Note des Schülers in der Klasse.

Hinweis: Korrelation erster Ordnung wird manchmal als partielle Korrelation bezeichnet . In diesem Tutorial wird erklärt, wie man Teilkorrelationen in Excel berechnet.

Korrelationen nullter Ordnung in einer Korrelationsmatrix

Wir erstellen eine Korrelationsmatrix. Wann immer für eine Reihe von Variablen die in der Matrix angezeigten Korrelationskoeffizienten immer Korrelationen nullter Ordnung sind, da es sich lediglich um die Korrelationen zwischen jeder paarweisen Kombination von Variablen handelt, ohne den Einfluss anderer Variablen zu berücksichtigen.

Betrachten Sie zum Beispiel unseren Datensatz aus dem vorherigen Beispiel:

Wenn wir für diesen Datensatz eine Korrelationsmatrix erstellen würden, würde diese so aussehen:

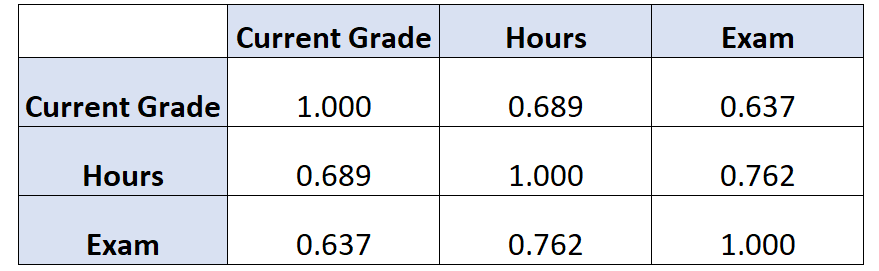
Die Art und Weise, dies zu interpretieren, ist:

• Die Korrelation zwischen der aktuellen Note und den gelernten Stunden beträgt 0,689 .
• Die Korrelation zwischen der aktuellen Punktzahl und der in der Prüfung erzielten Punktzahl beträgt 0,637 .
• Die Korrelation zwischen Lernstunden und Prüfungsergebnis beträgt 0,762 .

Jede dieser Korrelationen ist eine Korrelation nullter Ordnung .

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Korrelationskoeffizienten:

Einführung in den Pearson-Korrelationskoeffizienten
So lesen Sie eine Korrelationsmatrix
So berechnen Sie die partielle Korrelation in Excel