Korrelation vs. assoziation: was ist der unterschied?

Zwei Begriffe, die manchmal synonym verwendet werden, sind Korrelation und Assoziation . Im Bereich der Statistik haben diese beiden Begriffe jedoch leicht unterschiedliche Bedeutungen.

Insbesondere wenn wir das Wort Korrelation verwenden, sprechen wir normalerweise vom Pearson-Korrelationskoeffizienten . Es ist ein Maß für den linearen Zusammenhang zwischen zwei Zufallsvariablen X und Y. Es hat einen Wert zwischen -1 und 1, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Umgekehrt können Statistiker, wenn sie das Wort Assoziation verwenden, über jede Beziehung zwischen zwei Variablen sprechen, unabhängig davon, ob sie linear oder nichtlinear ist.

Um diese Idee zu veranschaulichen, betrachten Sie die folgenden Beispiele.

Visualisierung der Korrelation und Assoziation mit Punktwolken

Wir verwenden zwei Wörter, um die Korrelation zwischen zwei Zufallsvariablen zu beschreiben:

1 Richtung

• Positiv: Zwei Zufallsvariablen haben eine positive Korrelation, wenn Y tendenziell zunimmt, wenn X zunimmt.
• Negativ: Zwei Zufallsvariablen haben eine negative Korrelation, wenn Y tendenziell abnimmt, während X zunimmt.

2. Stärke

• Niedrig: Zwei Zufallsvariablen haben eine geringe Korrelation, wenn die Punkte in einem Streudiagramm dünn verteilt sind.
• Stark: Zwei Zufallsvariablen weisen eine starke Korrelation auf, wenn die Punkte in einem Streudiagramm eng beieinander gruppiert sind.

Die folgenden Streudiagramme veranschaulichen Beispiele für jeden Korrelationstyp:

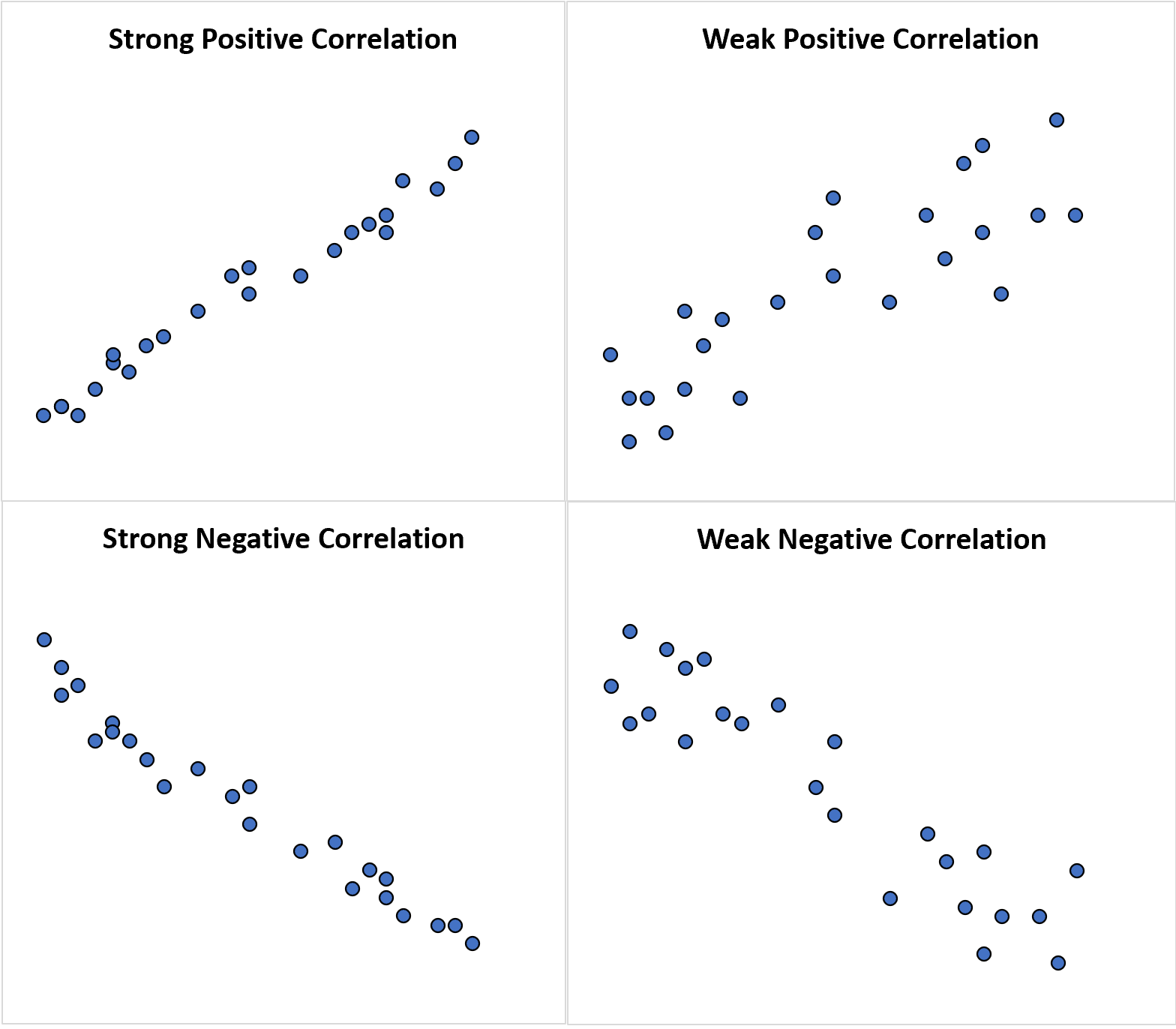
Im Vergleich zur Korrelation kann uns die Wortassoziation sagen, ob zwischen zwei Zufallsvariablen eine Beziehung besteht: linear oder nichtlinear.

Die folgenden Streudiagramme veranschaulichen einige Beispiele:

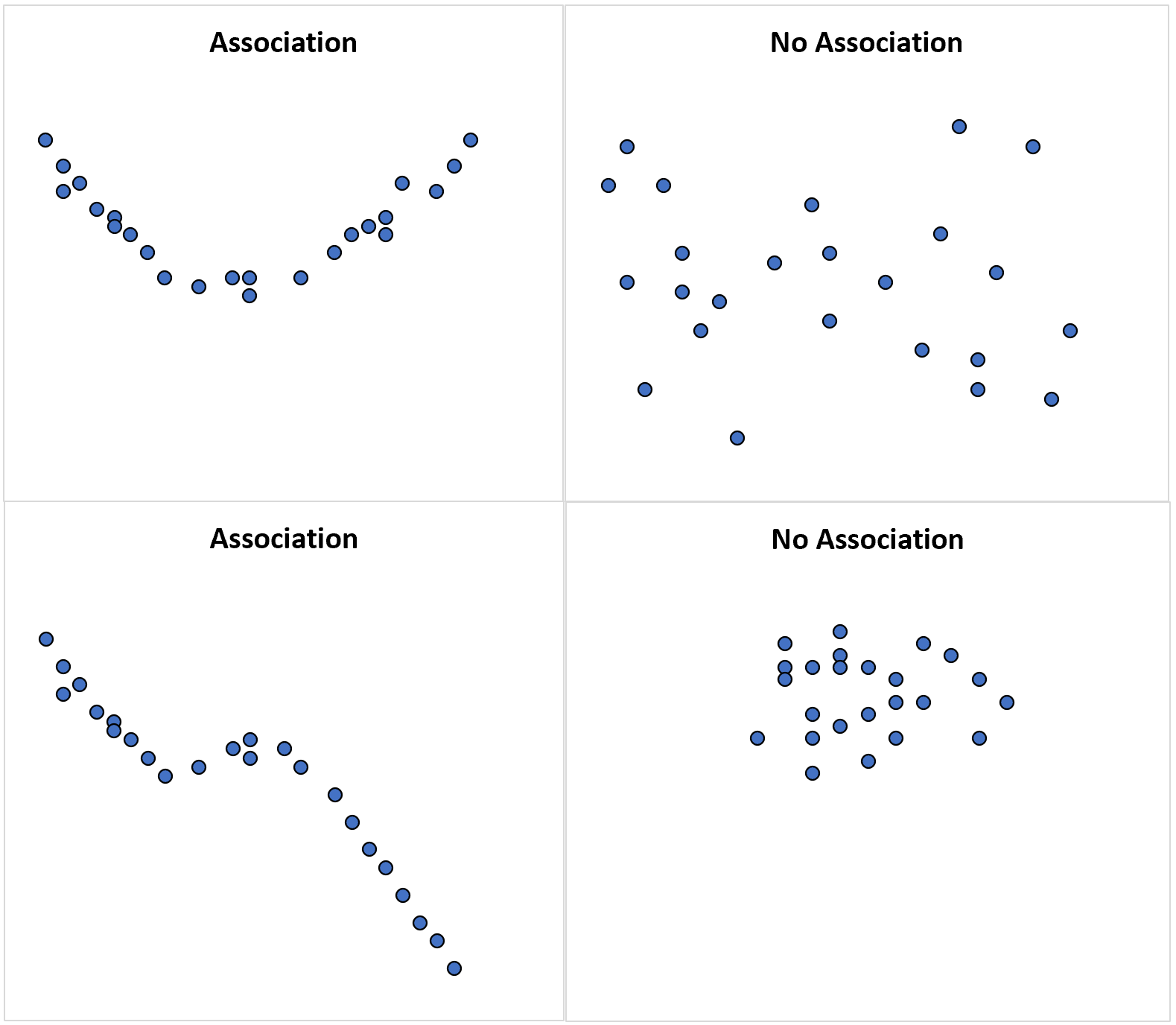
Das Streudiagramm in der oberen linken Ecke veranschaulicht eine quadratische Beziehung zwischen zwei Zufallsvariablen, was bedeutet, dass zwischen den beiden Variablen ein Zusammenhang besteht , dieser jedoch nicht linear ist.

Wenn wir die Korrelation zwischen den beiden Variablen berechnen würden, würde sie wahrscheinlich nahe Null liegen, da zwischen ihnen keine lineare Beziehung besteht.

Allerdings kann die bloße Kenntnis, dass die Korrelation zwischen den beiden Variablen Null ist, irreführend sein, da dadurch die Tatsache verschleiert wird, dass stattdessen eine nichtlineare Beziehung besteht.

Korrelation vs. Assoziation: eine Zusammenfassung

Die Begriffe Korrelation und Assoziation weisen folgende Gemeinsamkeiten und Unterschiede auf:

Ähnlichkeiten:

• Mit beiden Begriffen wird beschrieben, ob zwischen zwei Zufallsvariablen ein Zusammenhang besteht oder nicht.
• Beide Begriffe können Streudiagramme verwenden, um die Beziehung zwischen zwei Zufallsvariablen zu analysieren.

Unterschiede:

• Die Korrelation kann uns nur sagen, ob zwei Zufallsvariablen eine lineare Beziehung haben, während die Assoziation uns sagen kann, ob zwei Zufallsvariablen eine lineare oder nichtlineare Beziehung haben.
• Bei der Korrelation wird die Beziehung zwischen zwei Zufallsvariablen mithilfe einer Zahl zwischen -1 und 1 quantifiziert, bei der Assoziation wird jedoch keine bestimmte Zahl zur Quantifizierung einer Beziehung verwendet.

Zusätzliche Ressourcen

Eine Einführung in den Pearson-Korrelationskoeffizienten
Eine Einführung in Punktwolken
Korrelation vs. Regression: Was ist der Unterschied?