Korrelation vs. regression: was ist der unterschied?

Korrelation und Regression sind zwei verwandte, aber nicht völlig gleiche statistische Begriffe.

In diesem Tutorial geben wir eine kurze Erklärung beider Begriffe und erklären, wie ähnlich und unterschiedlich sie sind.

Was ist Korrelation?

Die Korrelation misst den linearen Zusammenhang zwischen zwei Variablen, x und y . Es hat einen Wert zwischen -1 und 1, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Angenommen, wir haben den folgenden Datensatz, der zwei Variablen enthält: (1) gelernte Stunden und (2) erhaltene Prüfungsergebnisse für 20 verschiedene Studenten:

Wenn wir ein Streudiagramm der Lernstunden im Vergleich zu den Prüfungsergebnissen erstellen würden, würde es so aussehen:

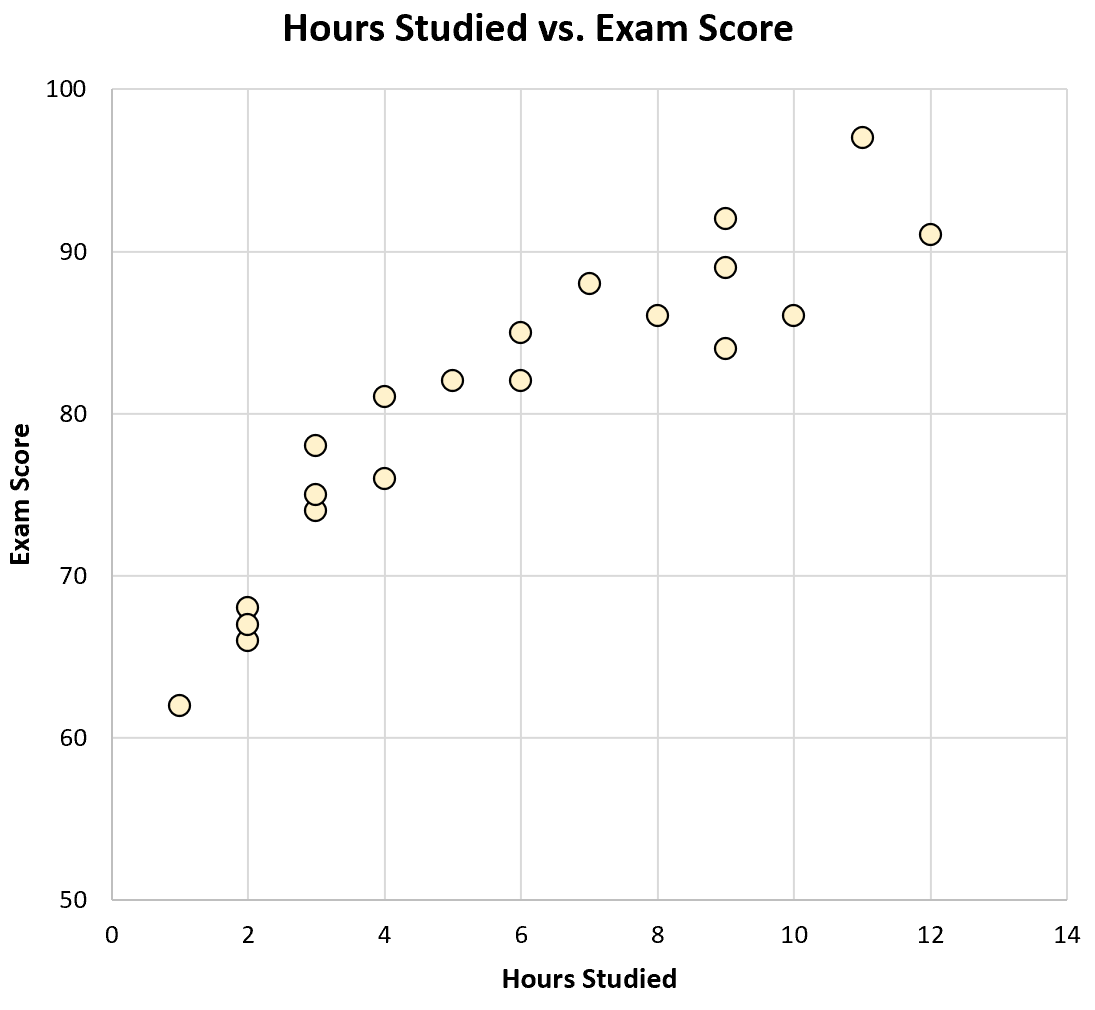
Wenn wir uns die Grafik ansehen, können wir erkennen, dass Studierende, die mehr lernen, bei Prüfungen tendenziell bessere Ergebnisse erzielen. Mit anderen Worten: Wir können visuell erkennen, dass zwischen den beiden Variablen eine positive Korrelation besteht.

Mithilfe eines Taschenrechners können wir erkennen, dass die Korrelation zwischen diesen beiden Variablen r = 0,915 beträgt. Da dieser Wert nahe bei 1 liegt, bestätigt dies, dass eine starke positive Korrelation zwischen den beiden Variablen besteht.

Was ist Regression?

Regression ist eine Methode, mit der wir verstehen können, wie sich eine Änderung der Werte der Variablen x auf die Werte der Variablen y auswirkt.

Ein Regressionsmodell verwendet eine Variable, x , als Prädiktorvariable und die andere Variable, y , als Antwortvariable . Anschließend wird eine Gleichung der folgenden Form ermittelt, die die Beziehung zwischen den beiden Variablen am besten beschreibt:

ŷ = b ₀ + b ₁ x

Gold:

• ŷ: der vorhergesagte Wert der Antwortvariablen
• b ₀ : Die Ordinate im Ursprung (der Wert von y, wenn x gleich Null ist)
• b ₁ : Der Regressionskoeffizient (der durchschnittliche Anstieg von y für einen Anstieg von x um eine Einheit)
• x: der Wert der Vorhersagevariablen

Betrachten Sie zum Beispiel unseren vorherigen Datensatz:

Mithilfe eines linearen Regressionsrechners stellen wir fest, dass die folgende Gleichung die Beziehung zwischen diesen beiden Variablen am besten beschreibt:

Voraussichtliche Prüfungspunktzahl = 65,47 + 2,58*(Studienstunden)

Die Art und Weise, diese Gleichung zu interpretieren, ist:

• Die voraussichtliche Prüfungspunktzahl für einen Studenten, der null Stunden studiert, beträgt 65,47 .
• Die durchschnittliche Steigerung der Prüfungspunktzahl, die mit einer zusätzlichen Unterrichtsstunde einhergeht, beträgt 2,58 .

Wir können diese Gleichung auch verwenden, um die Punktzahl vorherzusagen, die ein Schüler basierend auf der Anzahl der gelernten Stunden erhalten wird.

Beispielsweise sollte ein Student, der 6 Stunden lernt, eine Note von 80,95 erhalten:

Voraussichtliches Prüfungsergebnis = 65,47 + 2,58*(6) = 80,95 .

Wir können diese Gleichung auch als Linie in einem Streudiagramm darstellen:

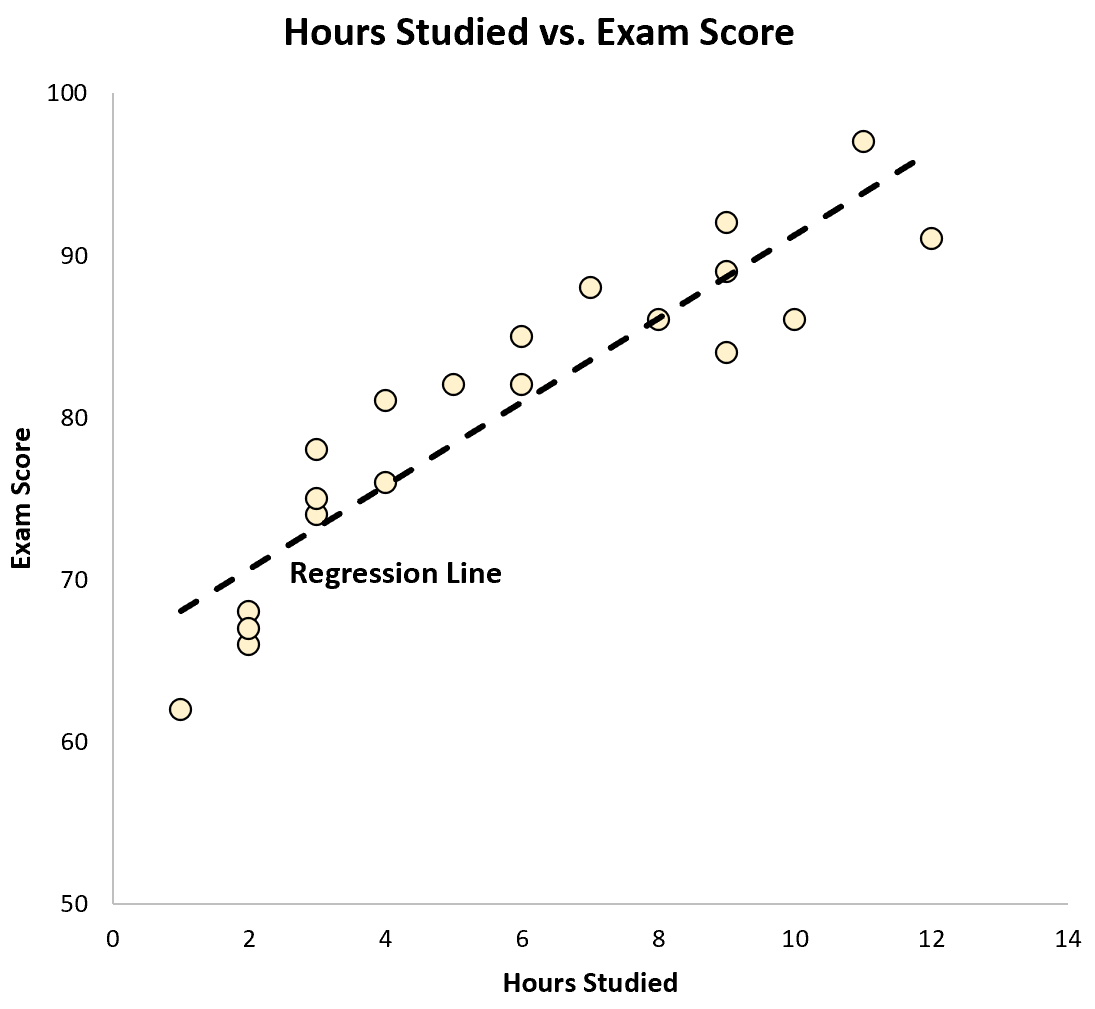
Wir können sehen, dass die Regressionsgerade recht gut zu den Daten „passt“.

Denken Sie daran, dass die Korrelation zwischen diesen beiden Variablen r = 0,915 betrug. Es stellt sich heraus, dass wir diesen Wert quadrieren können und eine Zahl namens „r-Quadrat“ erhalten, die den Gesamtanteil der Varianz in der Antwortvariablen beschreibt, der durch die Prädiktorvariable erklärt werden kann.

In diesem Beispiel ist r ² = 0,915 ² = 0,837 . Dies bedeutet, dass 83,7 % der Abweichungen in den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden können.

Korrelation vs. Regression: Ähnlichkeiten und Unterschiede

Hier ist eine Zusammenfassung der Ähnlichkeiten und Unterschiede zwischen Korrelation und Regression:

Ähnlichkeiten:

• Beide quantifizieren die Richtung einer Beziehung zwischen zwei Variablen.
• Beide quantifizieren die Stärke einer Beziehung zwischen zwei Variablen.

Unterschiede:

• Die Regression ist in der Lage, eine Ursache-Wirkungs-Beziehung zwischen zwei Variablen aufzuzeigen. Korrelation macht das nicht.
• Bei der Regression kann eine Gleichung verwendet werden, um den Wert einer Variablen basierend auf dem Wert einer anderen Variablen vorherzusagen. Korrelation macht das nicht.
• Bei der Regression wird eine Gleichung verwendet, um die Beziehung zwischen zwei Variablen zu quantifizieren. Die Korrelation verwendet eine einzelne Zahl.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten ausführlichere Erläuterungen zu den in diesem Artikel behandelten Themen.

Eine Einführung in den Pearson-Korrelationskoeffizienten
Eine Einführung in die einfache lineare Regression
Einfacher linearer Regressionsrechner
Was ist ein guter R-Quadrat-Wert?