So berechnen sie die korrelation zwischen kategorialen variablen

Wir verwenden häufig den Pearson-Korrelationskoeffizienten , um die Korrelation zwischen kontinuierlichen numerischen Variablen zu berechnen.

Wir müssen jedoch eine andere Metrik verwenden, um die Korrelation zwischen kategorialen Variablen zu berechnen, d. h. Variablen, die Namen oder Bezeichnungen annehmen, wie zum Beispiel:

• Familienstand (ledig, verheiratet, geschieden)
• Raucherstatus (Raucher, Nichtraucher)
• Augenfarbe (blau, braun, grün)

Es gibt drei häufig verwendete Maße zur Berechnung der Korrelation zwischen kategorialen Variablen:

1. Tetrachorische Korrelation: Wird zur Berechnung der Korrelation zwischen binären kategorialen Variablen verwendet.

2. Polychorische Korrelation: Wird zur Berechnung der Korrelation zwischen ordinalen kategorialen Variablen verwendet.

3. Cramer’s V: wird zur Berechnung der Korrelation zwischen nominalen kategorialen Variablen verwendet.

Die folgenden Abschnitte enthalten ein Beispiel für die Berechnung jeder dieser drei Messungen.

Metrik 1: Tetrachorische Korrelation

Mithilfe der tetrachorischen Korrelation wird die Korrelation zwischen binären kategorialen Variablen berechnet. Denken Sie daran, dass binäre Variablen Variablen sind, die nur einen von zwei möglichen Werten annehmen können.

Der tetrachorische Korrelationswert reicht von -1 bis 1, wobei -1 eine starke negative Korrelation anzeigt, 0 keine Korrelation anzeigt und 1 eine starke positive Korrelation anzeigt.

Angenommen, wir möchten wissen, ob das Geschlecht mit der Präferenz für eine politische Partei zusammenhängt. Wir nehmen also eine einfache Zufallsstichprobe von 100 Wählern und fragen sie nach ihrer Präferenz für eine politische Partei.

Die folgende Tabelle stellt die Ergebnisse der Umfrage dar:

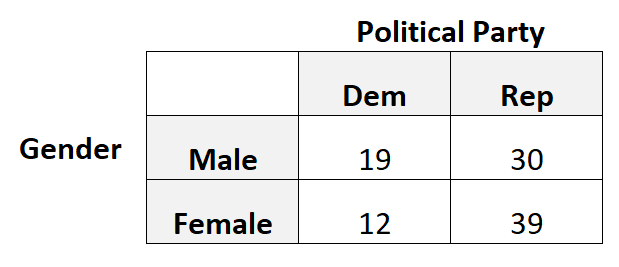
In diesem Szenario würden wir die tetrachorische Korrelation verwenden, da jede kategoriale Variable binär ist, das heißt, jede Variable kann nur zwei mögliche Werte annehmen.

Wir können den folgenden Code in R verwenden, um die tetrachorische Korrelation zwischen den beiden Variablen zu berechnen:

 library (psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow= 2 )

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

Die tetrachorische Korrelation beträgt 0,27 . Dieser Wert ist recht niedrig, was darauf hindeutet, dass (wenn überhaupt) ein schwacher Zusammenhang zwischen Geschlecht und Parteipräferenz besteht.

Metrik 2: Polychorische Korrelation

Mithilfe der polychorischen Korrelation wird die Korrelation zwischen ordinalen kategorialen Variablen berechnet. Denken Sie daran, dass Ordinalvariablen Variablen sind, deren mögliche Werte eine natürliche Reihenfolge haben.

Der Wert der polychorischen Korrelation reicht von -1 bis 1, wobei -1 eine starke negative Korrelation angibt, 0 keine Korrelation angibt und 1 eine starke positive Korrelation angibt.

Angenommen, Sie möchten wissen, ob zwei verschiedene Filmbewertungsagenturen eine hohe Korrelation zwischen ihren Filmbewertungen aufweisen.

Wir bitten jede Agentur, 20 verschiedene Filme auf einer Skala von 1 bis 3 zu bewerten, wobei 1 „schlecht“, 2 „schlecht“ und 3 „gut“ bedeutet.

Die folgende Tabelle zeigt die Ergebnisse:

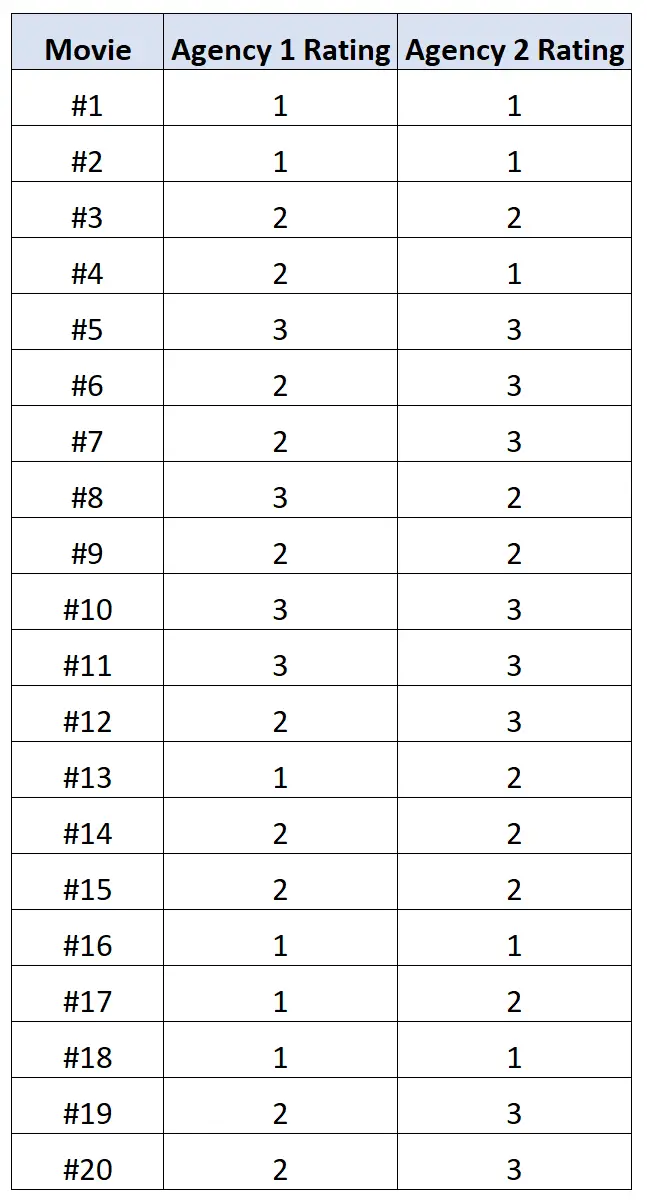
Wir können den folgenden Code in R verwenden, um die polychorische Korrelation zwischen den Bewertungen der beiden Agenturen zu berechnen:

 library (polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

Die polychorische Korrelation beträgt 0,78 . Dieser Wert ist recht hoch, was darauf hindeutet, dass zwischen den Bewertungen der einzelnen Agenturen ein starker positiver Zusammenhang besteht.

Metrik 3: Cramers V

Cramers V wird verwendet, um die Korrelation zwischen nominalen kategorialen Variablen zu berechnen. Denken Sie daran, dass nominale Variablen solche sind, die Kategoriebezeichnungen tragen, aber keine natürliche Reihenfolge haben.

Der Wert von Cramers V liegt zwischen 0 und 1, wobei 0 keinen Zusammenhang zwischen den Variablen und 1 einen starken Zusammenhang zwischen den Variablen anzeigt.

Nehmen wir zum Beispiel an, wir möchten wissen, ob ein Zusammenhang zwischen Augenfarbe und Geschlecht besteht. Wir befragen daher 50 Personen und kommen zu folgenden Ergebnissen:

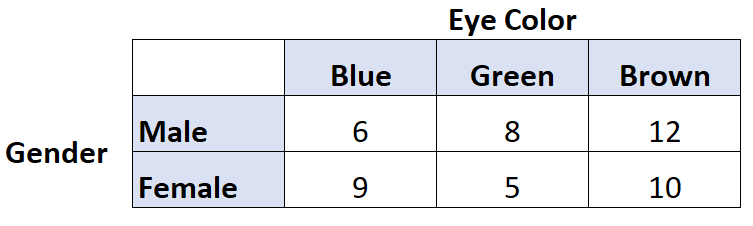
Wir können den folgenden Code in R verwenden, um Cramers V für diese beiden Variablen zu berechnen:

 library (rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )

#view table
data

     [,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

Es stellt sich heraus, dass Cramers V 0,1671 beträgt. Dieser Wert ist recht niedrig, was darauf hindeutet, dass ein schwacher Zusammenhang zwischen Geschlecht und Augenfarbe besteht.

Zusätzliche Ressourcen

Einführung in den Pearson-Korrelationskoeffizienten
Einführung in die tetrachorische Korrelation
Kategoriale oder quantitative Variablen: Was ist der Unterschied?
Messniveaus: nominal, ordinal, Intervall und Verhältnis