So berechnen sie die korrelation zwischen kontinuierlichen und kategorialen variablen

Wenn wir die Korrelation zwischen zwei kontinuierlichen Variablen berechnen möchten, verwenden wir im Allgemeinen den Pearson-Korrelationskoeffizienten .

Wenn wir jedoch die Korrelation zwischen einer kontinuierlichen Variablen und einer kategorialen Variablen berechnen möchten, können wir die sogenannte punktbiserielle Korrelation verwenden.

Die punktbiserielle Korrelation wird zur Berechnung der Korrelation zwischen einer binären kategorialen Variablen (einer Variablen, die nur zwei Werte annehmen kann) und einer kontinuierlichen Variablen verwendet und weist die folgenden Eigenschaften auf:

• Die Punkt-Biserial-Korrelation kann zwischen -1 und 1 variieren.
• Für jede durch die binäre Variable erstellte Gruppe wird angenommen, dass die kontinuierliche Variable normalverteilt mit gleichen Varianzen ist.
• Für jede durch die Binärvariable erstellte Gruppe wird davon ausgegangen, dass es keine extremen Ausreißer gibt.

Das folgende Beispiel zeigt, wie man eine Punkt-Biserial-Korrelation in der Praxis berechnet.

Beispiel: Berechnung einer Punkt-Biserial-Korrelation

Angenommen, ein Universitätsprofessor möchte feststellen, ob ein Zusammenhang zwischen Geschlecht und Punktzahl bei einer bestimmten Eignungsprüfung besteht.

Er sammelt folgende Daten von 12 Jungen und 12 Mädchen in seiner Klasse:

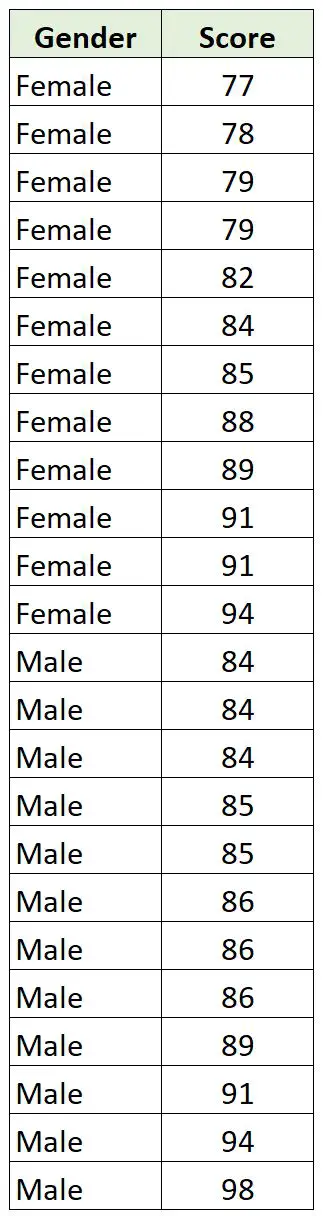
Da es sich bei Geschlecht um eine kategoriale Variable und bei Score um eine kontinuierliche Variable handelt, ist es sinnvoll, eine punktbiserielle Korrelation zwischen den beiden Variablen zu berechnen.

Der Professor kann jede beliebige Statistiksoftware (einschließlich Excel, R, Python, SPSS, Stata) verwenden, um die punktbiserielle Korrelation zwischen den beiden Variablen zu berechnen.

Der folgende Code zeigt, wie die Punkt-Biserial-Korrelation in R berechnet wird, wobei für die Geschlechtsvariable der Wert 0 zur Darstellung von Frauen und 1 zur Darstellung von Männern verwendet wird:

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

Aus dem Ergebnis können wir ersehen, dass der Punkt-Biserial-Korrelationskoeffizient 0,281 beträgt und der entsprechende p-Wert 0,1833 beträgt.

Da der Korrelationskoeffizient positiv ist, bedeutet dies, dass eine positive Korrelation zwischen Geschlecht und Punktzahl besteht.

Da wir Männer mit 1 und Frauen mit 0 kodiert haben, deutet dies darauf hin, dass die Werte für Männer tendenziell höher sind (d. h. die Werte steigen tendenziell mit zunehmendem Geschlecht). » von 0 bis 1).

Da der p-Wert jedoch nicht kleiner als 0,05 ist, ist dieser Korrelationskoeffizient statistisch nicht signifikant.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie die punktbiserielle Korrelation mit unterschiedlicher Statistiksoftware berechnet wird:

So berechnen Sie die Punkt-Biserial-Korrelation in Excel
So berechnen Sie die Punkt-Biserial-Korrelation in R
So berechnen Sie die Punkt-Biserial-Korrelation in Python