Klasseninterner korrelationskoeffizient: definition + beispiel

Ein Intraclass-Korrelationskoeffizient (ICC) wird verwendet, um die Zuverlässigkeit der Ergebnisse in Studien zu messen, in denen es zwei oder mehr Bewerter gibt.

Der Wert eines ICC kann zwischen 0 und 1 liegen, wobei 0 für keine Zuverlässigkeit unter den Bewertern steht und 1 für vollkommene Zuverlässigkeit unter den Bewertern.

Einfach ausgedrückt wird ein ICC verwendet, um festzustellen, ob Artikel (oder Themen) von verschiedenen Bewertern zuverlässig bewertet werden können.

Es gibt verschiedene Versionen eines ICC, die abhängig von den folgenden drei Faktoren berechnet werden können:

• Modell: Einweg-Zufallseffekte, Zwei-Wege-Zufallseffekte oder Zwei-Wege-Mischeffekte
• Art der Beziehung: Konsistenz oder absolute Übereinstimmung
• Einheit: Einzelbewerter oder Durchschnitt der Bewerter

Hier eine kurze Beschreibung der drei verschiedenen Modelle :

1. Einweg-Random-Effects-Modell: Dieses Modell geht davon aus, dass jeder Proband von einer anderen Gruppe zufällig ausgewählter Bewerter bewertet wird. Bei diesem Modell werden Bewerter als Quelle zufälliger Effekte betrachtet. Dieses Modell wird in der Praxis selten angewendet, da für die Beurteilung jedes Fachs im Allgemeinen dieselbe Gruppe von Prüfern eingesetzt wird.

2. Zwei-Wege-Zufallseffektmodell: Dieses Modell geht davon aus, dass eine Gruppe von Bewertern k zufällig aus einer Population ausgewählt und dann zur Bewertung der Probanden verwendet wird. Bei diesem Modell werden Bewerter und Probanden als Quellen zufälliger Effekte betrachtet. Dieses Modell wird häufig verwendet, wenn wir unsere Ergebnisse auf Bewerter übertragen möchten, die denen in der Studie ähneln.

3. Zwei-Wege-Mixed-Effects-Modell: Dieses Modell geht außerdem davon aus, dass eine Gruppe von Bewertern k zufällig aus einer Population ausgewählt und dann zur Bewertung der Probanden verwendet wird. Dieses Modell geht jedoch davon aus, dass die von uns ausgewählte Gruppe von Bewertern die einzigen Bewerter ist, die von Interesse sind. Das bedeutet, dass wir unsere Ergebnisse nicht auf andere Bewerter übertragen möchten, die möglicherweise ähnliche Merkmale wie die in der Studie verwendeten Bewerter aufweisen.

Hier ist eine kurze Beschreibung der beiden verschiedenen Arten von Beziehungen, die wir messen möchten:

1. Konsistenz: Wir sind an systematischen Unterschieden zwischen den Bewertungen der Richter interessiert (z. B. haben Richter ähnliche Themen als niedrig und hoch bewertet?)

2. Absolute Übereinstimmung: Uns interessieren die absoluten Unterschiede zwischen den Wertungen der Richter (z. B. was ist der absolute Unterschied zwischen den Werten von Richter A und Richter B?)

Hier ist eine kurze Beschreibung der beiden verschiedenen Einheiten , die uns interessieren könnten:

1. Einzelner Rezensent: Wir möchten nur die Bewertungen eines einzelnen Rezensenten als Grundlage für die Messung verwenden.

2. Bewerterdurchschnitt: Als Grundlage für die Messung wollen wir den Durchschnitt aller Bewertungen der Juroren verwenden.

Hinweis: Wenn Sie den Grad der Übereinstimmung zwischen zwei Bewertern messen möchten, die bei einem dichotomen Ergebnis jedes der Elemente verfehlen, sollten Sie stattdessen Cohens Kappa verwenden.

So interpretieren Sie den Intraclass-Korrelationskoeffizienten

So interpretieren Sie den Wert eines klasseninternen Korrelationskoeffizienten nach Koo & Li :

• Weniger als 0,50: schlechte Zuverlässigkeit
• Zwischen 0,5 und 0,75: Mäßige Zuverlässigkeit
• Zwischen 0,75 und 0,9: Gute Zuverlässigkeit
• Größer als 0,9: Hervorragende Zuverlässigkeit

Das folgende Beispiel zeigt, wie ein Intraclass-Korrelationskoeffizient in der Praxis berechnet wird.

Beispiel: Berechnung des Intraclass-Korrelationskoeffizienten

Angenommen, vier verschiedene Richter werden gebeten, die Qualität von zehn verschiedenen Hochschulaufnahmeprüfungen zu bewerten. Die Ergebnisse sind unten dargestellt:

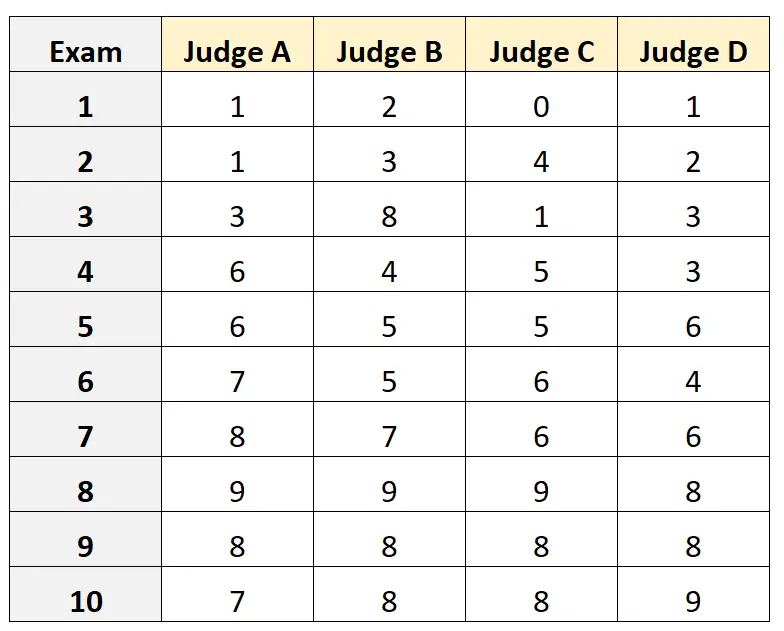
Angenommen, die vier Richter wurden zufällig aus einer Gruppe qualifizierter Richter für die Aufnahmeprüfung ausgewählt und wir wollten die absolute Übereinstimmung zwischen den Richtern messen und die Ergebnisse aus der Perspektive nur eines Bewerters als Grundlage für unsere Messung verwenden.

Wir können den folgenden Code in R verwenden, um ein bidirektionales Zufallseffektmodell anzupassen, indem wir die absolute Übereinstimmung als Beziehung zwischen den Bewertern und die einzelne Einheit als interessierende Einheit verwenden:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

Der klasseninterne Korrelationskoeffizient (ICC) betrug 0,782 .

Basierend auf den Faustregeln zur Interpretation des ICC würden wir zu dem Schluss kommen, dass ein ICC von 0,782 darauf hinweist, dass Prüfungen von verschiedenen Bewertern mit „guter“ Zuverlässigkeit bewertet werden können.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten detaillierte Erklärungen zur Berechnung des ICC in verschiedenen Statistiksoftware:

So berechnen Sie den klasseninternen Korrelationskoeffizienten in Excel
So berechnen Sie den klasseninternen Korrelationskoeffizienten in R
So berechnen Sie den klasseninternen Korrelationskoeffizienten in Python