So erstellen sie eine korrelationsmatrix in r (4 beispiele)

Eine Korrelationsmatrix ist eine quadratische Tabelle, die die Korrelationskoeffizienten zwischen Variablen in einem Datensatz anzeigt.

Es bietet eine schnelle Möglichkeit, die Stärke linearer Beziehungen zu verstehen, die zwischen Variablen in einem Datensatz bestehen.

Es gibt vier gängige Methoden zum Erstellen einer Korrelationsmatrix in R:

Methode 1: die Cor-Funktion (um eine einfache Matrix von Korrelationskoeffizienten zu erhalten)

 cor(df)

Methode 2: die rcorr-Funktion (um die p-Werte der Korrelationskoeffizienten zu erhalten)

 library (Hmisc)

rcorr( as.matrix (df))

Methode 3: die Corrplot-Funktion (zur Visualisierung der Korrelationsmatrix)

 library (corplot)

corrplot(cor(df))

Methode 4: die ggcorrplot-Funktion (zur Visualisierung der Korrelationsmatrix)

 library (ggcorrplot)

ggcorrplot(cor(df))

Die folgenden Beispiele zeigen, wie jede Methode mit dem folgenden Datenrahmen in R verwendet wird:

 #create data frame
df <- data. frame (assists=c(4, 5, 5, 6, 7, 8, 8, 10),
                 rebounds=c(12, 14, 13, 7, 8, 8, 9, 13),
                 points=c(22, 24, 26, 26, 29, 32, 20, 14))

#view data frame
df

  assists rebound points
1 4 12 22
2 5 14 24
3 5 13 26
4 6 7 26
5 7 8 29
6 8 8 32
7 8 9 20
8 10 13 14

Beispiel 1: Die cor-Funktion

Mit der R-Base-Funktion cor() können wir eine Korrelationsmatrix erstellen, die die Korrelationskoeffizienten zwischen den einzelnen Variablen in unserem Datenrahmen anzeigt:

 #create correlation matrix
cor(df)

            assists rebound points
assists 1.0000000 -0.2448608 -0.3295730
rebounds -0.2448608 1.0000000 -0.5220917
points -0.3295730 -0.5220917 1.0000000

Die Korrelationskoeffizienten entlang der Diagonalen der Tabelle sind alle gleich 1, da jede Variable perfekt mit sich selbst korreliert.

Alle anderen Korrelationskoeffizienten geben die Korrelation zwischen verschiedenen paarweisen Kombinationen von Variablen an. Zum Beispiel:

• Der Korrelationskoeffizient zwischen Assists und Rebounds beträgt -0,245 .
• Der Korrelationskoeffizient zwischen Assists und Punkten beträgt -0,330 .
• Der Korrelationskoeffizient zwischen Rebounds und Punkten beträgt -0,522 .

Beispiel 2: die rcorr-Funktion

Wir können die Funktion rcorr() aus dem Hmisc- Paket in R verwenden, um eine Korrelationsmatrix zu erstellen, die die Korrelationskoeffizienten zwischen jeder Variablen in unserem Datenrahmen zeigt:

 library (Hmisc)

#create matrix of correlation coefficients and p-values
rcorr( as.matrix (df))

         assists rebound points
assists 1.00 -0.24 -0.33
rebounds -0.24 1.00 -0.52
points -0.33 -0.52 1.00

n=8 

P
         assists rebound points
assists 0.5589 0.4253
rebounds 0.5589 0.1844
points 0.4253 0.1844

Die erste Matrix zeigt die Korrelationskoeffizienten zwischen den Variablen und die zweite Matrix zeigt die entsprechenden p-Werte.

Beispielsweise beträgt der Korrelationskoeffizient zwischen Assists und Rebounds -0,24 und der p-Wert dieses Korrelationskoeffizienten beträgt 0,5589 .

Dies sagt uns, dass die Korrelation zwischen den beiden Variablen negativ ist, aber es handelt sich nicht um eine statistisch signifikante Korrelation, da der p-Wert nicht weniger als 0,05 beträgt.

Beispiel 3: Die corrplot-Funktion

Wir können die Funktion corrplot() aus dem Paket corrplot in R verwenden, um die Korrelationsmatrix zu visualisieren:

 library (corplot)

#visualize correlation matrix
corrplot(cor(df))

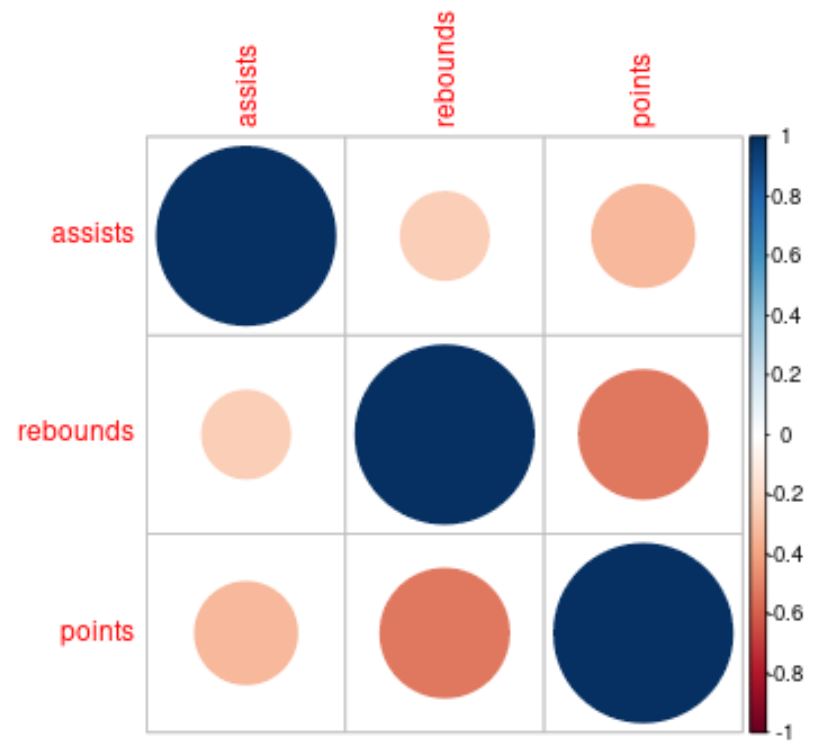
Die Farbe und Größe der Kreise in der Korrelationsmatrix helfen uns, die Korrelationen zwischen den einzelnen Variablen zu visualisieren.

Beispielsweise ist der Kreis, in dem sich die Assists- und Rebounds-Variablen schneiden, klein und hellrot, was uns sagt, dass die Korrelation schwach und negativ ist.

Beispiel 4: Die corrplot-Funktion

Wir können die Funktion ggcorrplot() aus dem Paket ggcorrplot in R verwenden, um die Korrelationsmatrix zu visualisieren:

 library (ggcorrplot)

#visualize correlation matrix
ggcorrplot(cor(df))

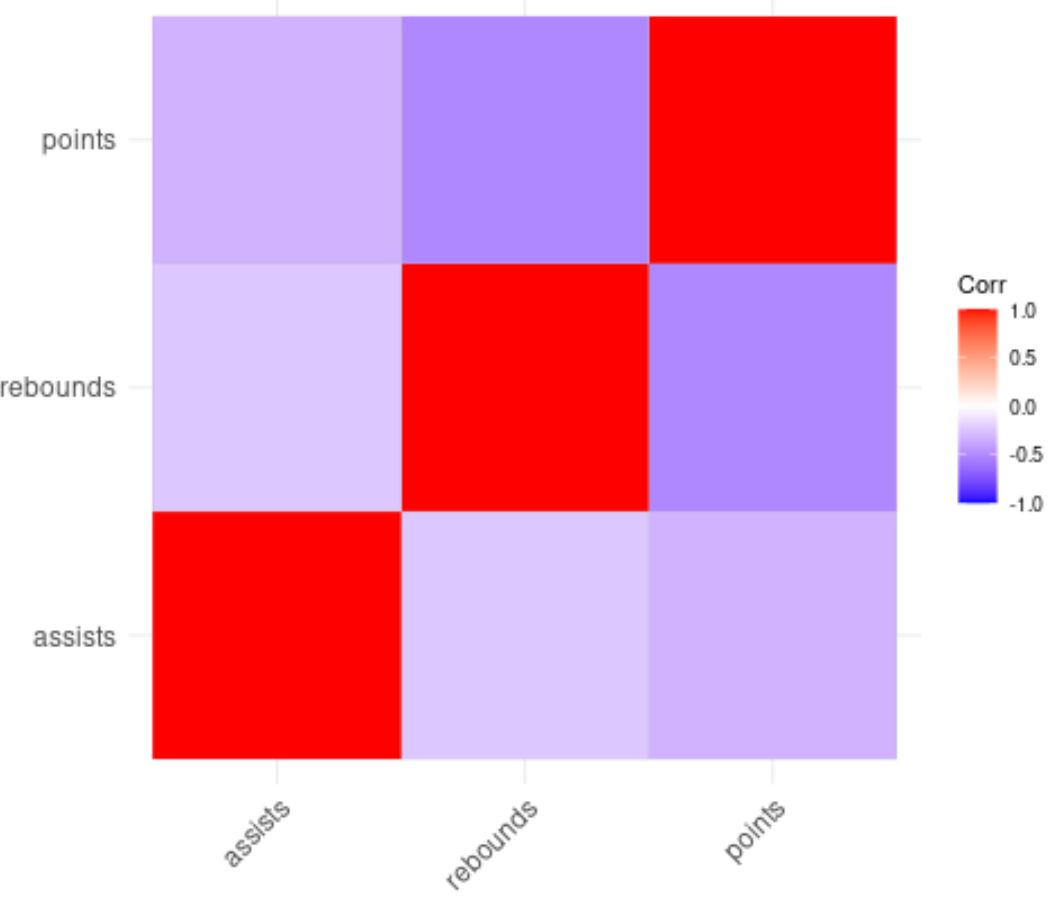
Die Farbe der Quadrate in der Korrelationsmatrix hilft uns, die Korrelationen zwischen den einzelnen Variablen zu visualisieren.

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie Sie andere häufige Aufgaben in R ausführen:

So berechnen Sie die Spearman-Rangkorrelation in R
So berechnen Sie die partielle Korrelation in R
So berechnen Sie die gleitende Korrelation in R