So führen sie einen korrelationstest in r durch (mit beispielen)

Eine Möglichkeit, die Beziehung zwischen zwei Variablen zu quantifizieren, ist die Verwendung des Pearson-Korrelationskoeffizienten , der ein Maß für den linearen Zusammenhang zwischen zwei Variablen ist .

Es nimmt immer einen Wert zwischen -1 und 1 an, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Um festzustellen, ob ein Korrelationskoeffizient statistisch signifikant ist, können Sie den entsprechenden t-Score und p-Wert berechnen.

Die Formel zur Berechnung des t-Scores eines Korrelationskoeffizienten (r) lautet:

t = r * √ n-2 / √ 1-r ²

Der p-Wert wird als entsprechender zweiseitiger p-Wert für die t-Verteilung mit n-2 Freiheitsgraden berechnet.

Beispiel: Korrelationstest in R

Um festzustellen, ob der Korrelationskoeffizient zwischen zwei Variablen statistisch signifikant ist, können Sie einen Korrelationstest in R mit der folgenden Syntax durchführen:

cor.test(x, y, method=c(„pearson“, „kendall“, „spearman“))

Gold:

• x, y: digitale Datenvektoren.
• Methode: Methode zur Berechnung der Korrelation zwischen zwei Vektoren. Der Standardwert ist „Pearson“.

Angenommen, wir haben die folgenden zwei Vektoren in R:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Bevor wir einen Korrelationstest zwischen den beiden Variablen durchführen, können wir ein schnelles Streudiagramm erstellen, um ihre Beziehung zu visualisieren:

 #create scatterplot
plot(x, y, pch= 16 )

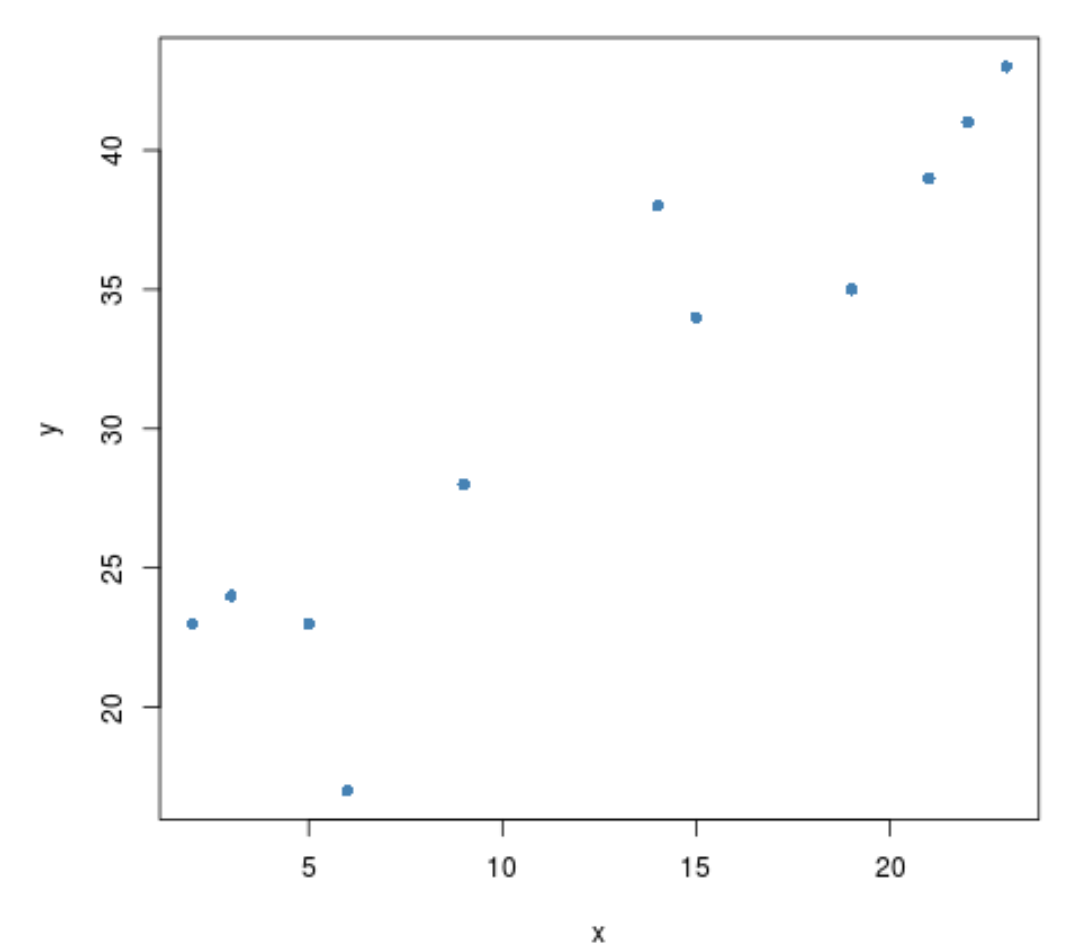
Es scheint eine positive Korrelation zwischen den beiden Variablen zu bestehen. Das heißt, wenn das eine zunimmt, nimmt auch das andere tendenziell zu.

Um festzustellen, ob diese Korrelation statistisch signifikant ist, können wir einen Korrelationstest durchführen:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

Der Korrelationskoeffizient zwischen den beiden Vektoren beträgt 0,9279869 .

Die Teststatistik beträgt 7,8756 und der entsprechende p-Wert beträgt 1,35e-05 .

Da dieser Wert weniger als 0,05 beträgt, haben wir genügend Belege dafür, dass die Korrelation zwischen den beiden Variablen statistisch signifikant ist.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Korrelationskoeffizienten:

Eine Einführung in den Pearson-Korrelationskoeffizienten
Was gilt als „starke“ Korrelation?
Die fünf Hypothesen der Pearson-Korrelation