Kovarianz

Von Dr. Benjamin Anderson August 5, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was Kovarianz ist und wie sie berechnet wird. Sie finden die Kovarianzformel sowie ein Beispiel zur Berechnung der Kovarianz eines Datensatzes. Zusätzlich können Sie mit dem Online-Rechner am Ende die Kovarianz beliebiger Datenreihen berechnen.

Was ist Kovarianz?

In der Statistik ist Kovarianz ein Wert, der den Grad der gemeinsamen Variation zweier Zufallsvariablen angibt. Mit anderen Worten: Kovarianz wird verwendet, um die Abhängigkeit zwischen zwei Variablen zu analysieren.

Die Kovarianz ist gleich der Summe der Produkte der Differenzen zwischen den Daten der beiden Variablen und ihren jeweiligen Mittelwerten dividiert durch die Gesamtzahl der Daten.

👉 Mit dem Rechner unten können Sie die Kovarianz eines beliebigen Datensatzes berechnen.

Die Interpretation des Kovarianzwertes ist sehr einfach:

Wenn die Kovarianz positiv ist , bedeutet dies, dass eine Abhängigkeit zwischen den beiden Variablen besteht. Wenn also eine Variable an Wert zunimmt, nimmt auch die andere Variable zu und umgekehrt.
Wenn die Kovarianz negativ ist , bedeutet dies, dass die Beziehung zwischen den beiden Variablen negativ ist. Wenn also der Wert einer Variablen zunimmt, nimmt der Wert der anderen Variablen ab und umgekehrt.
Wenn die Kovarianz Null ist (oder ihr Wert nahe bei Null liegt), bedeutet dies, dass zwischen den beiden Variablen keine Beziehung besteht. Mit anderen Worten: Die beiden Zufallsvariablen sind unabhängig.

So berechnen Sie die Kovarianz

Um die Kovarianz einer Datenreihe zu berechnen, müssen folgende Schritte durchgeführt werden:

Berechnen Sie den Durchschnitt jeder Variablen separat.
Ermitteln Sie für jede Variable die Differenz zwischen jedem ihrer Werte und dem Mittelwert der Variablen.
Multiplizieren Sie die im vorherigen Schritt berechneten Differenzen für jeden Datenpunkt.
Addieren Sie alle im vorherigen Schritt erhaltenen Ergebnisse.
Teilen Sie durch die Gesamtzahl der Daten. Der erhaltene Wert ist die Kovarianz der Datenreihe.

Zusammenfassend lautet die Formel zur Berechnung der Kovarianz zwischen zwei Variablen wie folgt:

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

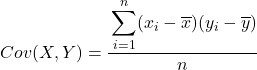
Eine dringend empfohlene Methode zum Extrahieren der Kovarianz zwischen zwei Variablen besteht darin, eine Tabelle mit allen Datenpaaren zu erstellen und für jeden der oben erläuterten Schritte eine Spalte hinzuzufügen. Auf diese Weise werden Ihre Berechnungen viel besser organisiert und Sie werden besser verstehen, was Sie tun.

Beispiel einer Kovarianzberechnung

Unter Berücksichtigung der Definition der Kovarianz finden Sie unten ein schrittweises Beispiel für die Berechnung dieser Art von statistischem Maß. Ziel ist es, das Konzept der Kovarianz besser zu verstehen und die Korrelation zwischen zwei Variablen zu analysieren.

Berechnen Sie die Kovarianz des folgenden statistischen Datensatzes:

Zuerst müssen wir das arithmetische Mittel jeder Variablen berechnen. Dazu dividieren wir die Summe der Werte jeder Variablen durch die Gesamtzahl der Daten.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ Siehe: Mittelwert der arithmetischen Formel

Sobald wir den Mittelwert jeder Zufallsvariablen ermittelt haben, können wir der Datentabelle die folgenden Spalten hinzufügen, um die Kovarianz zu ermitteln:

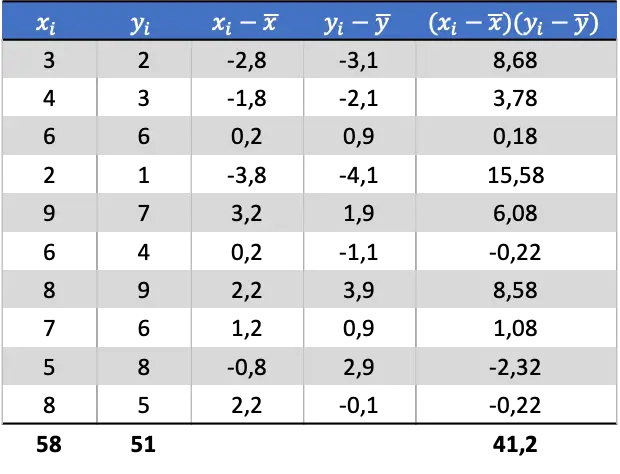
Um die Kovarianz der beiden Variablen zu bestimmen, müssen Sie also die Summe der letzten Spalte durch die Anzahl der Datenpaare dividieren:

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

In diesem Fall ist der Kovarianzwert positiv, was bedeutet, dass eine direkte Abhängigkeit zwischen den beiden untersuchten Zufallsvariablen besteht. Wäre der Kovarianzwert jedoch negativ gewesen, würde dies bedeuten, dass die Abhängigkeit zwischen den beiden Variablen umgekehrt ist. Und schließlich: Wenn der Kovarianzwert Null ist oder sehr nahe bei Null liegt, bedeutet dies, dass zwischen den beiden Variablen keine lineare Beziehung besteht.

Wie Sie anhand der Lösung dieses Beispiels sehen können, ist es sehr nützlich, ein Computerprogramm wie Excel zu verwenden, um die Spalten zur Tabelle hinzuzufügen und die Berechnungen schnell durchzuführen. Andernfalls dauert es bei manueller Berechnung der Operationen viel länger, die Kovarianz zu ermitteln.

Kovarianzrechner

Geben Sie einen Satz statistischer Daten in den folgenden Rechner ein, um die Kovarianz zwischen zwei Variablen zu berechnen. Sie müssen die Datenpaare trennen, sodass im ersten Feld nur die Werte einer Variablen und im zweiten Feld nur die Werte der zweiten Variablen stehen.

Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Kovarianzeigenschaften

Kovarianz hat die folgenden Eigenschaften:

Die Kovarianz zwischen einer Zufallsvariablen und einer Konstante ist Null.

$Cov(X,a)=0$

Die Kovarianz einer Variablen und sich selbst entspricht der Varianz dieser Variablen.

$Cov(X,X)=Var(X)$

➤ Siehe: Was ist Varianz?

Die Kovarianz erfüllt die Symmetrieeigenschaft, sodass die Kovarianz der Variablen X und Y gleich der Kovarianz der Variablen Y und X ist. Die Reihenfolge der Variablen hat keinen Einfluss auf das Ergebnis der Kovarianz.

$Cov(X,Y)=Cov(Y,X)$

Wenn die Variablen mit Konstanten multipliziert werden, können Sie zunächst die Kovarianz berechnen und dann das Ergebnis mit den Konstanten multiplizieren.

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

Das Hinzufügen von Termen zu Variablen hat keinen Einfluss auf das Kovarianzergebnis.

$Cov(a+X,b+Y)=Cov(X+Y)$

Die Kovarianz zwischen zwei Zufallsvariablen hängt mit ihren mathematischen Erwartungen zusammen. Die Kovarianz zwischen den Variablen X und Y ist gleich dem mathematischen Erwartungswert des Produkts von X und Y minus dem Produkt des mathematischen Erwartungswerts jeder Variablen.

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

Bei der Arbeit mit Variablen wird hinsichtlich der Kovarianz folgender algebraischer Ausdruck gefüllt:

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen