So erstellen sie eine kovarianzmatrix in google sheets
Kovarianz ist ein Maß dafür, wie Änderungen einer Variablen mit Änderungen einer zweiten Variablen verbunden sind. Genauer gesagt ist es ein Maß für den Grad, in dem zwei Variablen linear miteinander verbunden sind.
Die Formel zur Berechnung der Kovarianz zwischen zwei Variablen, X und Y, lautet:
COV( X , Y ) = Σ(x- x )(y- y ) / n
Eine Kovarianzmatrix ist eine quadratische Matrix, die die Kovarianz zwischen vielen verschiedenen Variablen zeigt. Dies kann eine nützliche Methode sein, um zu verstehen, wie verschiedene Variablen in einem Datensatz zusammenhängen.
Das folgende Beispiel zeigt, wie Sie in Google Sheets eine Kovarianzmatrix für einen bestimmten Datensatz erstellen.
So erstellen Sie eine Kovarianzmatrix in Google Sheets
Nehmen wir an, wir haben den folgenden Datensatz, der die Testergebnisse von 10 verschiedenen Schülern in drei Fächern zeigt: Mathematik, Naturwissenschaften und Geschichte.
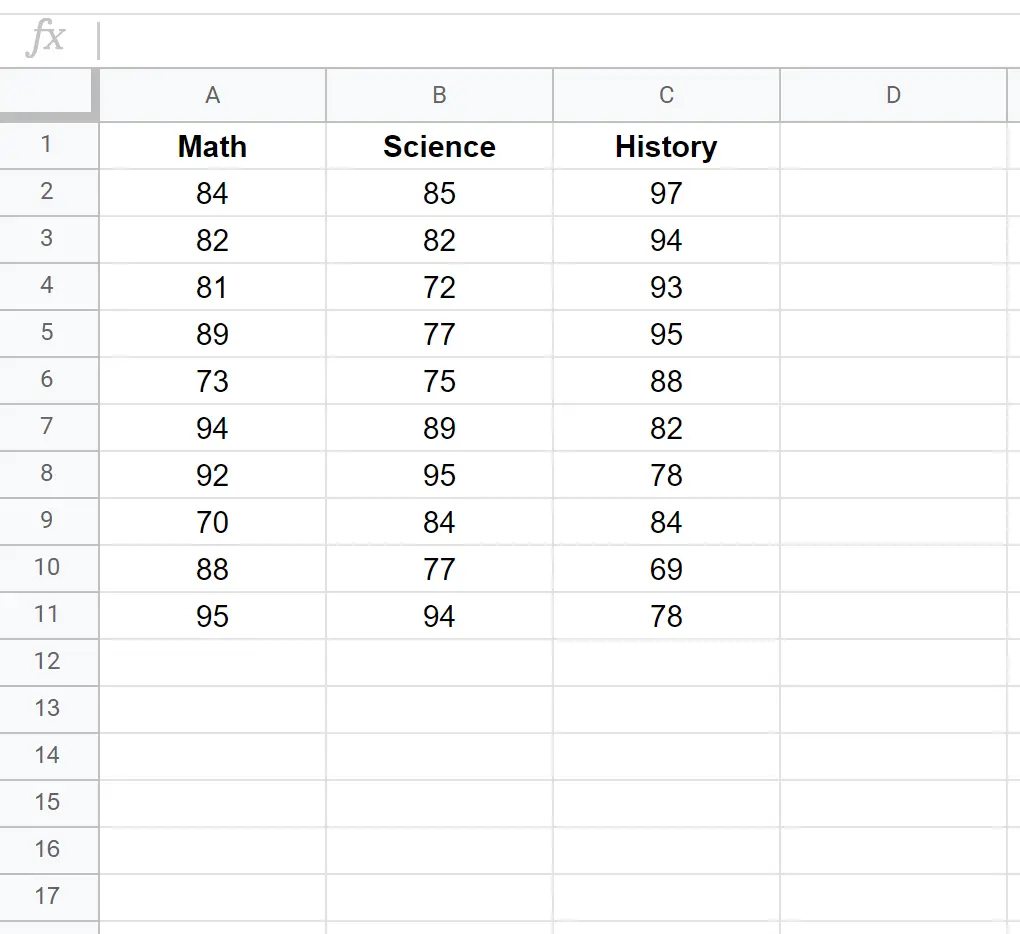
Um eine Kovarianzmatrix für diesen Datensatz zu erstellen, können wir die Funktion COVAR() mit der folgenden Syntax verwenden:
COVAR(data_y, data_x)
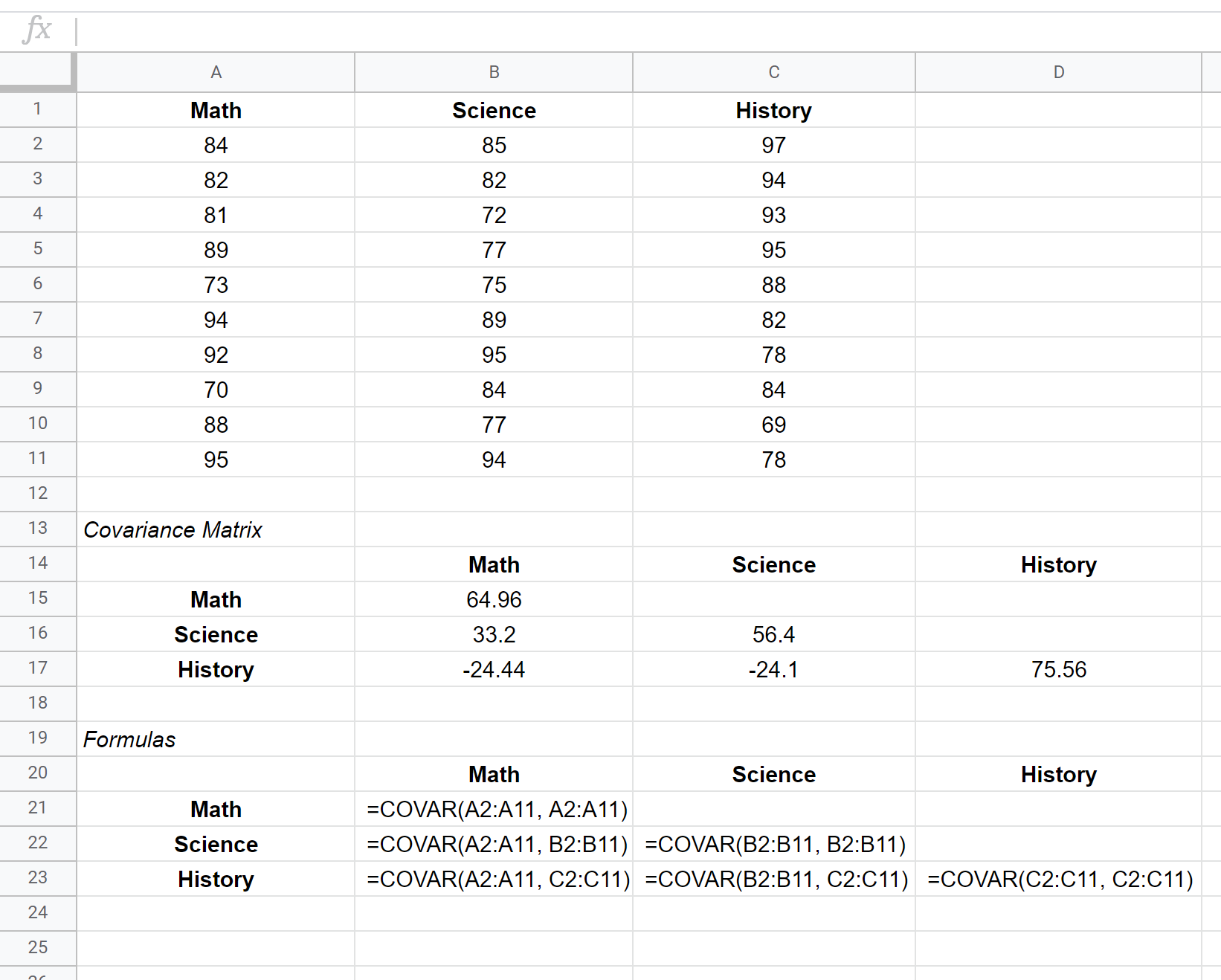
Die Kovarianzmatrix für diesen Datensatz wird in den Zellen B15:D17 angezeigt, während die zur Erstellung der Kovarianzmatrix verwendeten Formeln in den Zellen B21:D23 unten angezeigt werden:
So interpretieren Sie eine Kovarianzmatrix
Sobald wir eine Kovarianzmatrix haben, ist es einfach, die Matrixwerte zu interpretieren.
Die Werte entlang der Diagonalen der Matrix sind einfach die Varianzen jedes Subjekts. Zum Beispiel:
- Die Varianz der Mathematikergebnisse beträgt 64,96
- Die Varianz der naturwissenschaftlichen Ergebnisse beträgt 56,4
- Die historische Score-Varianz beträgt 75,56

Die anderen Werte der Matrix stellen die Kovarianzen zwischen den verschiedenen Subjekten dar. Zum Beispiel:
- Die Kovarianz zwischen den Ergebnissen in Mathematik und Naturwissenschaften beträgt 33,2.
- Die Kovarianz zwischen Mathematik- und Geschichtsergebnissen beträgt -24,44.
- Die Kovarianz zwischen den Ergebnissen in Naturwissenschaften und Geschichte beträgt -24,1.

Eine positive Zahl für die Kovarianz zeigt an, dass zwei Variablen tendenziell gleichzeitig zunehmen oder abnehmen. Beispielsweise weisen Mathematik und Naturwissenschaften eine positive Kovarianz (33,2) auf, was darauf hindeutet, dass Schüler, die in Mathematik gute Ergebnisse erzielen, tendenziell auch in Naturwissenschaften gute Ergebnisse erzielen. Ebenso tendieren Schüler, die in Mathematik schlecht abschneiden, auch in den Naturwissenschaften zu schlechten Leistungen.
Eine negative Zahl für die Kovarianz bedeutet, dass eine zweite Variable tendenziell abnimmt, wenn eine Variable zunimmt. Beispielsweise haben Mathematik und Geschichte eine negative Kovarianz (-24,44), was darauf hindeutet, dass Schüler, die in Mathematik gute Ergebnisse erzielen, tendenziell schlechte Ergebnisse in Geschichte erzielen. Ebenso erzielen Schüler, die in Mathematik schlechte Ergebnisse erzielen, tendenziell gute Ergebnisse in Geschichte.
Zusätzliche Ressourcen
So erstellen Sie eine Kovarianzmatrix in Excel
So erstellen Sie eine Kovarianzmatrix in R
So erstellen Sie eine Kovarianzmatrix in Python
So erstellen Sie eine Kovarianzmatrix in SPSS