Kreisdiagramm

In diesem Artikel erfahren Sie, was ein Kreisdiagramm ist, wie man ein Kreisdiagramm erstellt und eine Schritt-für-Schritt-Übung für diesen Diagrammtyp. Darüber hinaus können Sie die Eigenschaften der Kreisdiagramme erkennen.

Was ist ein Kreisdiagramm?

Ein Tortendiagramm , auch Tortendiagramm genannt, ist eine Art statistisches Diagramm, das zur visuellen Darstellung von Prozentsätzen und Proportionen dient. Genauer gesagt werden die Daten in einem Kreisdiagramm durch Teile eines Kreises dargestellt, sodass der Winkel jedes Käses proportional zu seiner Häufigkeit ist.

Je häufiger also ein Wert vorkommt, desto größer ist sein Anteil am Kreisdiagramm.

In der Statistik sind Kreisdiagramme sehr nützlich, um qualitative Daten in einem Diagramm darzustellen, und sie ermöglichen es Ihnen auch, schnell Schlussfolgerungen zu ziehen.

Es ist zu beachten, dass das Kreisdiagramm viele verschiedene Namen hat, wie z . B. Tortendiagramm, Pizzadiagramm, Tortendiagramm, Käsediagramm oder sogar 360-Grad-Diagramm.

So erstellen Sie ein Kreisdiagramm

Basierend auf der Definition eines Kreisdiagramms zeigt dieser Abschnitt, wie man ein Diagramm dieses Typs erstellt:

1. Sammeln Sie statistische Daten und erstellen Sie die entsprechende Häufigkeitstabelle.
2. Berechnen Sie den Winkel jedes Sektors des Diagramms mit der folgenden Formel



Gold



ist der Winkel des Sektors i ,



seine absolute Häufigkeit und



die Gesamtzahl der Daten.

3. Stellen Sie anhand der berechneten Winkel die Sektoren mithilfe eines Winkelmessers in einem kreisförmigen Diagramm dar.
4. Berechnen Sie den Prozentsatz jedes Sektors mit der folgenden Formel:



Gold



ist der Prozentsatz des Sektors i ,



seine absolute Häufigkeit und



die Gesamtzahl der Daten.

5. Geben Sie in der Grafik den Prozentsatz jedes Sektors an.

Beispiel für ein Kreisdiagramm

Damit Sie sehen können, wie ein Kreisdiagramm aufgebaut ist, lasse ich Ihnen unten ein Beispiel, das Schritt für Schritt erklärt wird.

• 50 Personen wurden nach ihrer Lieblingsstadt befragt und die Daten in der folgenden Tabelle zusammengestellt. Stellen Sie diese statistischen Daten in einem Kreisdiagramm dar.

Zunächst müssen Sie den Winkel finden, der jedem Käse entspricht. Dazu wenden wir die folgende Formel an:

Als Beispiel wird der Winkel berechnet, der dem ersten Wert in der Datentabelle entspricht:

Sobald wir den Winkel kennen, stellen Sie einfach den Kreissektor mit einem Winkelmesser dar:

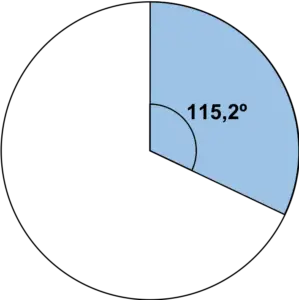
Wir wiederholen den gleichen Schritt für alle Werte in der Tabelle:

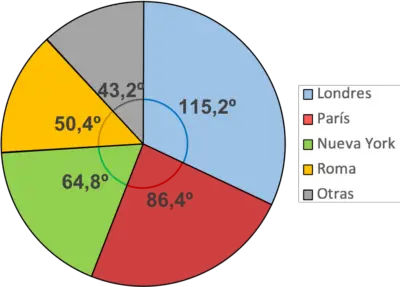
Es wird empfohlen, jeden Sektor mit einer Farbe zu versehen, um das Diagramm leichter verständlich zu machen. Ebenso sollten Sie eine Legende hinzufügen, um die Bedeutung jeder Farbe im Diagramm anzuzeigen.

Nachdem wir die Käsesorten grafisch dargestellt haben, müssen wir den Prozentsatz jedes einzelnen Käses berechnen, um ihn in das Diagramm einzutragen. Dazu verwenden wir die folgende Formel:

Der Prozentsatz jedes Sektors beträgt daher:

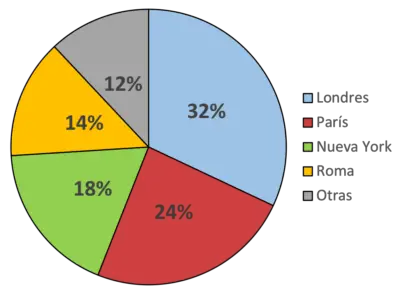
Mit diesem Kreisdiagramm zeigen wir an, dass beispielsweise die Farbe Blau die Stadt London darstellt und der Ort ist, den die meisten Menschen bevorzugen (32 % der Menschen). Die Farbe Grün hingegen repräsentiert New York, die Lieblingsstadt von 18 % der Befragten.

Kreisdiagrammfunktionen

Die Eigenschaften des Camemberts sind wie folgt:

• Das Kreisdiagramm eignet sich sehr gut zur Darstellung qualitativer Daten.
• Es gibt jedoch andere Arten statistischer Diagramme, die sich besser für die Darstellung quantitativer Variablen oder Zeitreihen eignen.
• Darüber hinaus kann in einem Kreisdiagramm nur eine Variable dargestellt werden, was den Vergleich von Variablen erschwert.
• Das Kreisdiagramm ist sehr anschaulich und ermöglicht eine schnelle Analyse und Schlussfolgerungen.
• Das Lesen des Diagramms ist schwierig, wenn es viele Sektoren gibt oder einige sehr klein sind. In einem solchen Fall wird empfohlen, die kleinen Sektoren in einem einzigen Sektor mit der Bezeichnung „Andere“ zusammenzufassen.