So berechnen sie die kreuzkorrelation in r

Kreuzkorrelation ist eine Möglichkeit, den Grad der Ähnlichkeit zwischen einer Zeitreihe und einer verzögerten Version einer anderen Zeitreihe zu messen.

Diese Art der Korrelation ist für die Berechnung nützlich, da sie uns sagen kann, ob Werte in einer Zeitreihe zukünftige Werte in einer anderen Zeitreihe vorhersagen. Mit anderen Worten: Es kann uns sagen, ob eine Zeitreihe ein Frühindikator für eine andere Zeitreihe ist.

Diese Art der Korrelation wird in vielen verschiedenen Bereichen verwendet, darunter:

Wirtschaft: Der Verbrauchervertrauensindex (CCI) gilt als Frühindikator für das Bruttoinlandsprodukt (BIP) eines Landes. Wenn beispielsweise der CCI in einem bestimmten Monat hoch ist, ist das BIP wahrscheinlich x Monate später höher.

Unternehmen: Marketingausgaben werden oft als Frühindikator für zukünftige Geschäftseinnahmen angesehen. Wenn ein Unternehmen beispielsweise in einem Quartal ungewöhnlich viel Geld für Marketing ausgibt, sollte der Gesamtumsatz x Quartale später hoch sein.

Biologie: Die Gesamtverschmutzung der Meere gilt als führender Indikator für die Population einer bestimmten Schildkrötenart. Wenn beispielsweise die Verschmutzung in einem bestimmten Jahr höher ist, wird erwartet, dass die Gesamtschildkrötenpopulation x Jahre später zurückgeht.

Das folgende Beispiel zeigt, wie die Kreuzkorrelation zwischen zwei Zeitreihen in R berechnet wird.

Beispiel: So berechnen Sie die Kreuzkorrelation in R

Angenommen, wir haben die folgende Zeitreihe in R, die die gesamten Marketingausgaben (in Tausend) für ein bestimmtes Unternehmen sowie den Gesamtumsatz (in Tausend) für 12 aufeinanderfolgende Monate zeigt:

 #define data
marketing <- c(3, 4, 5, 5, 7, 9, 13, 15, 12, 10, 8, 8)
revenue <- c(21, 19, 22, 24, 25, 29, 30, 34, 37, 40, 35, 30)

Wir können die Kreuzkorrelation für jede Verzögerung zwischen den beiden Zeitreihen mithilfe der Funktion ccf() wie folgt berechnen:

 #calculate cross correlation
ccf(marketing, revenue)

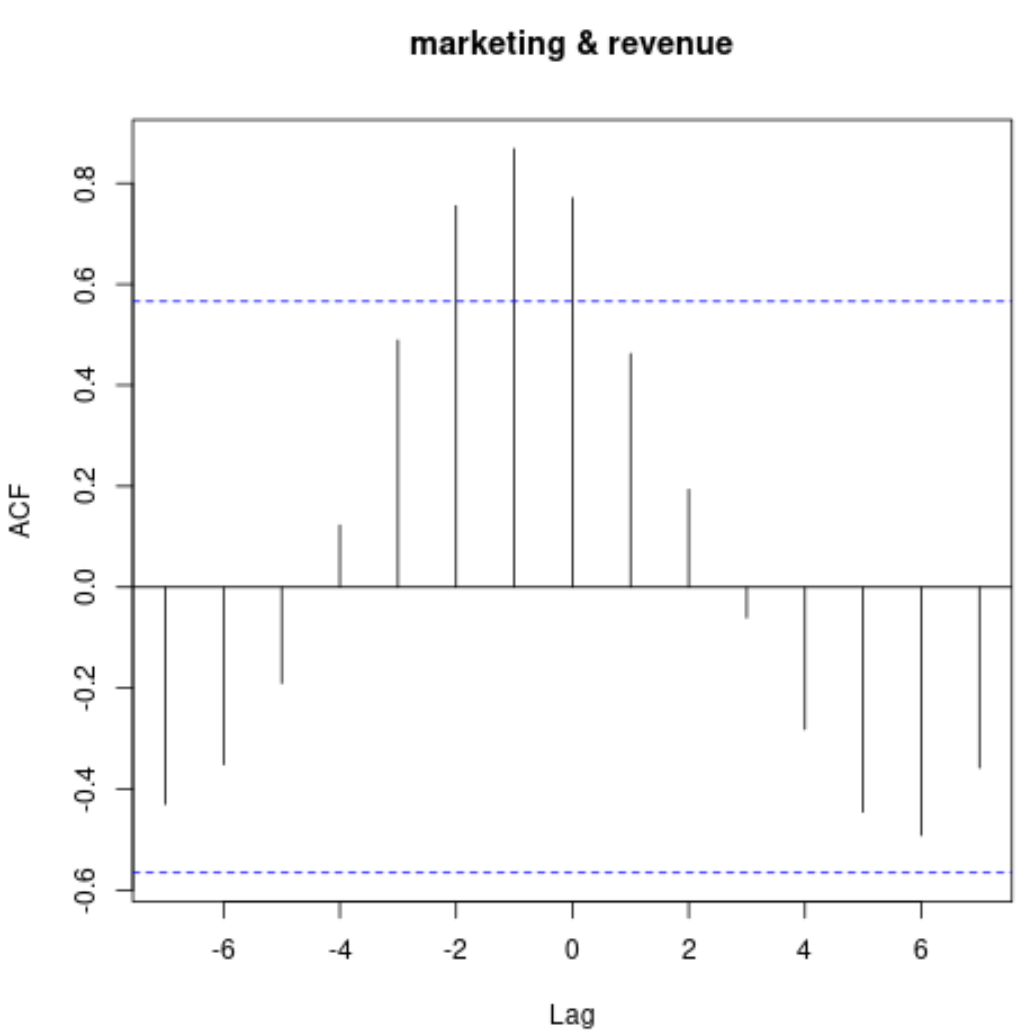
Dieses Diagramm zeigt die Korrelation zwischen den beiden Zeitreihen mit unterschiedlichen Verzögerungen.

Um die tatsächlichen Korrelationswerte anzuzeigen, können wir die folgende Syntax verwenden:

 #display cross correlation values
print (ccf(marketing, revenue))

Autocorrelations of series 'X', by lag

    -7 -6 -5 -4 -3 -2 -1 0 1 2 3 
-0.430 -0.351 -0.190 0.123 0.489 0.755 0.868 0.771 0.462 0.194 -0.061 
     4 5 6 7 
-0.282 -0.445 -0.492 -0.358

So interpretieren Sie diese Ausgabe:

• Die Kreuzkorrelation bei Verzögerung 0 beträgt 0,771 .
• Die Kreuzkorrelation bei Verzögerung 1 beträgt 0,462 .
• Die Kreuzkorrelation bei Verzögerung 2 beträgt 0,194 .
• Die Kreuzkorrelation bei Verzögerung 3 beträgt -0,061 .

Und so weiter.

Beachten Sie, dass die Korrelation zwischen den beiden Zeitreihen mit Verzögerungen von -2 bis 2 recht positiv ist, was uns sagt, dass die Marketingausgaben in einem bestimmten Monat einen guten Vorhersagewert für den Umsatz ein und zwei Monate später haben.

Dies macht intuitiv Sinn: Wir gehen davon aus, dass hohe Marketingausgaben in einem bestimmten Monat einen Anstieg des Umsatzes in den nächsten zwei Monaten vorhersagen.

Zusätzliche Ressourcen

So berechnen Sie die Autokorrelation in R
So berechnen Sie die partielle Korrelation in R
So berechnen Sie die gleitende Korrelation in R