Chauvenet-kriterium: definition und beispiel

Ein Ausreißer ist eine Beobachtung , die ungewöhnlich weit von anderen Werten in einem Datensatz entfernt ist. Ausreißer können problematisch sein, da sie die Ergebnisse einer Analyse beeinflussen können.

Eine Möglichkeit, Ausreißer in einem Datensatz zu identifizieren, ist die Verwendung des Chauvenet-Kriteriums , das den folgenden Prozess verwendet:

1. Berechnen Sie für jeden einzelnen Wert x _i im Datensatz die Abweichung vom Mittelwert wie folgt:

Abweichung = |x _i – x | /S

Dabei ist x der Stichprobenmittelwert und s die Stichprobenstandardabweichung.

2. Vergleichen Sie die Abweichungen jedes einzelnen Werts mit den kritischen Werten in der folgenden Chauvenet-Kriterientabelle. Melden Sie bei einzelnen Datenwerten mit Abweichungen, die größer sind als die in der Tabelle gefundenen, diese Datenwerte als Ausreißer.

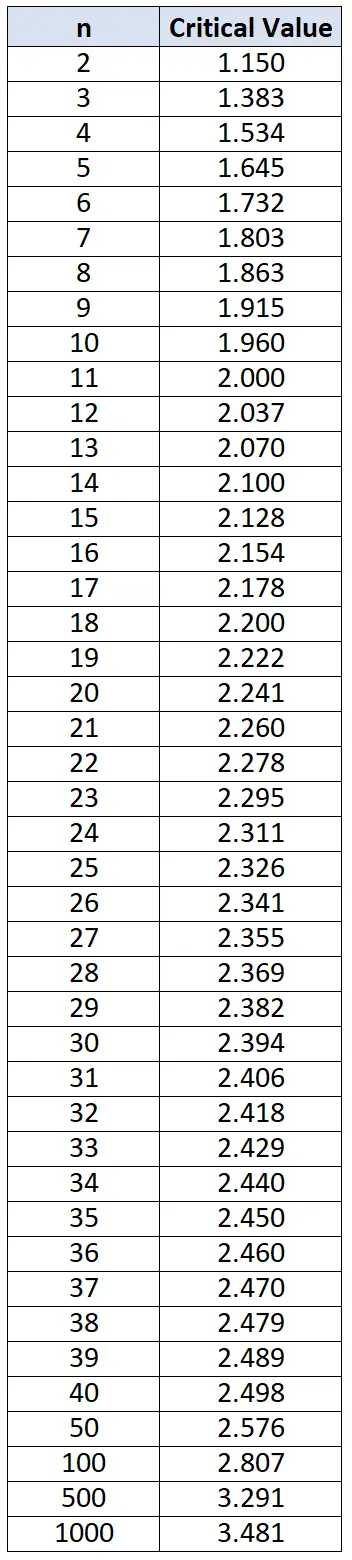
Das Chauvenet-Kriterium: ein Beispiel

Angenommen, wir haben den folgenden Datensatz mit 15 Werten:

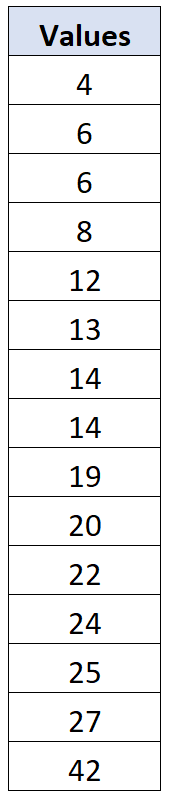
Der Stichprobenmittelwert für diesen Datensatz beträgt x = 17,067 und die Stichprobenstandardabweichung beträgt s = 10,096 . Für jeden einzelnen Datenwert können wir seine Abweichung wie folgt berechnen:

Abweichung = |x _i – x | /S

Zum Beispiel:

• Der erste Datenwert hätte eine Abweichung von |4 – 17,067| / 10.096 = 1.294 .
• Der erste Datenwert hätte eine Abweichung von |6 – 17,067| / 10,096 = 1,096 .

Und so weiter.

Wir können dieselbe Formel verwenden, um die Abweichung jedes einzelnen Datenwerts zu berechnen:

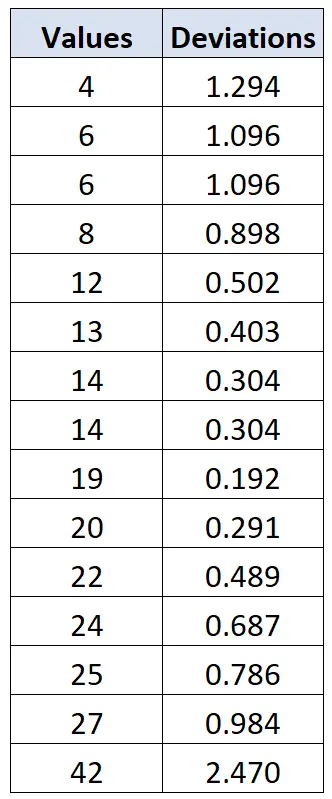
Wir können uns dann auf die Chauvenet-Kriterientabelle beziehen und feststellen, dass der kritische Wert, der einer Stichprobengröße von n=15 entspricht, 2,128 ist. Daher kann jeder Wert mit einer Abweichung von mehr als 2,128 als Ausreißer betrachtet werden.

Es stellt sich heraus, dass der Wert 42 eine Abweichung von mehr als 2,128 aufweist:

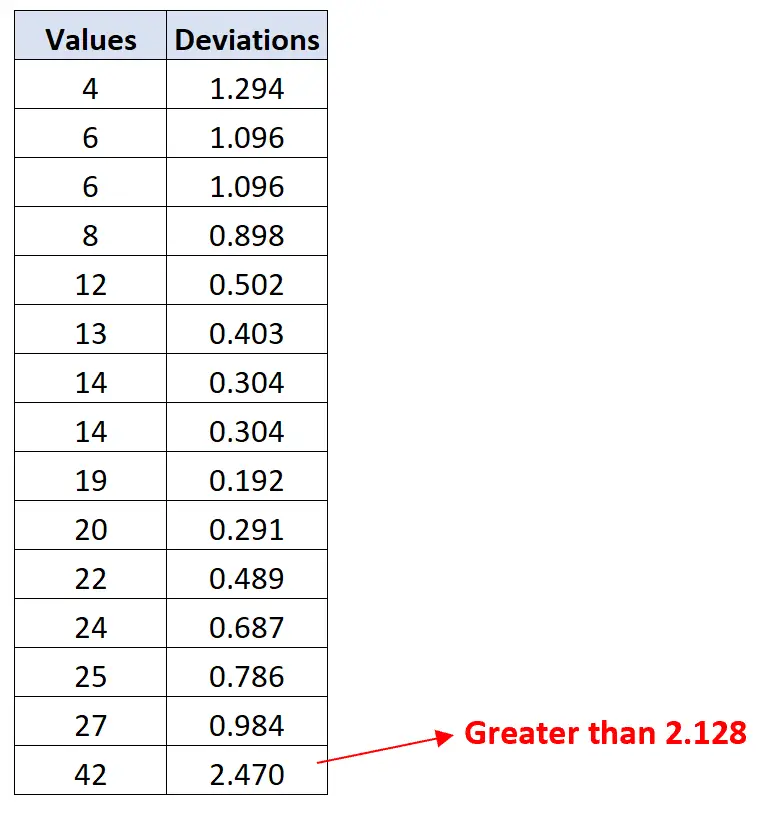
Somit ist der Wert 42 der einzige Ausreißer in diesem Datensatz.

Vorsichtsmaßnahmen hinsichtlich der Verwendung des Chauvenet-Kriteriums

Das Chauvenet-Kriterium geht davon aus, dass die Werte in einem Datensatznormalverteilt sind. Wenn diese Annahme nicht erfüllt ist, ist die Verwendung des Chauvenet-Kriteriums zur Identifizierung von Ausreißern wahrscheinlich nicht gültig.

Wenn Sie diese Methode verwenden und feststellen, dass es sich bei einem Wert um einen Ausreißer handelt, müssen Sie zunächst sicherstellen, dass der Wert nicht auf einen Dateneingabefehler zurückzuführen ist. Manchmal werden Daten einfach falsch eingegeben.

Wenn es sich bei dem Wert wirklich um einen Ausreißer handelt, können Sie ihn entfernen, wenn er erhebliche Auswirkungen auf Ihre Gesamtanalyse hat. Erwähnen Sie bei der Meldung Ihrer Ergebnisse unbedingt, dass Sie einen Ausreißer entfernt haben.

Darüber hinaus sollte diese Methode nur einmal für einen bestimmten Datensatz verwendet werden. Angenommen, wir verwenden dieses Kriterium, um den Wert 42 im vorherigen Beispiel als Ausreißer zu identifizieren und diesen Wert aus dem Datensatz zu entfernen.

Wir sollten dann nicht den Stichprobenmittelwert und die Stichprobenstandardabweichung neu berechnen und die Abweichungen erneut berechnen, um weitere Ausreißer zu finden.