Was ist krummlinige regression? (definition & beispiele)

Als krummlinige Regression bezeichnet man jedes Regressionsmodell, das versucht, eine Kurve statt einer geraden Linie anzupassen.

Zu den gängigen Beispielen für krummlinige Regressionsmodelle gehören:

Quadratische Regression: wird verwendet, wenn eine quadratische Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen besteht. In der grafischen Darstellung sieht diese Art von Beziehung in einem Streudiagramm wie ein „U“ oder ein umgekehrtes „U“ aus:

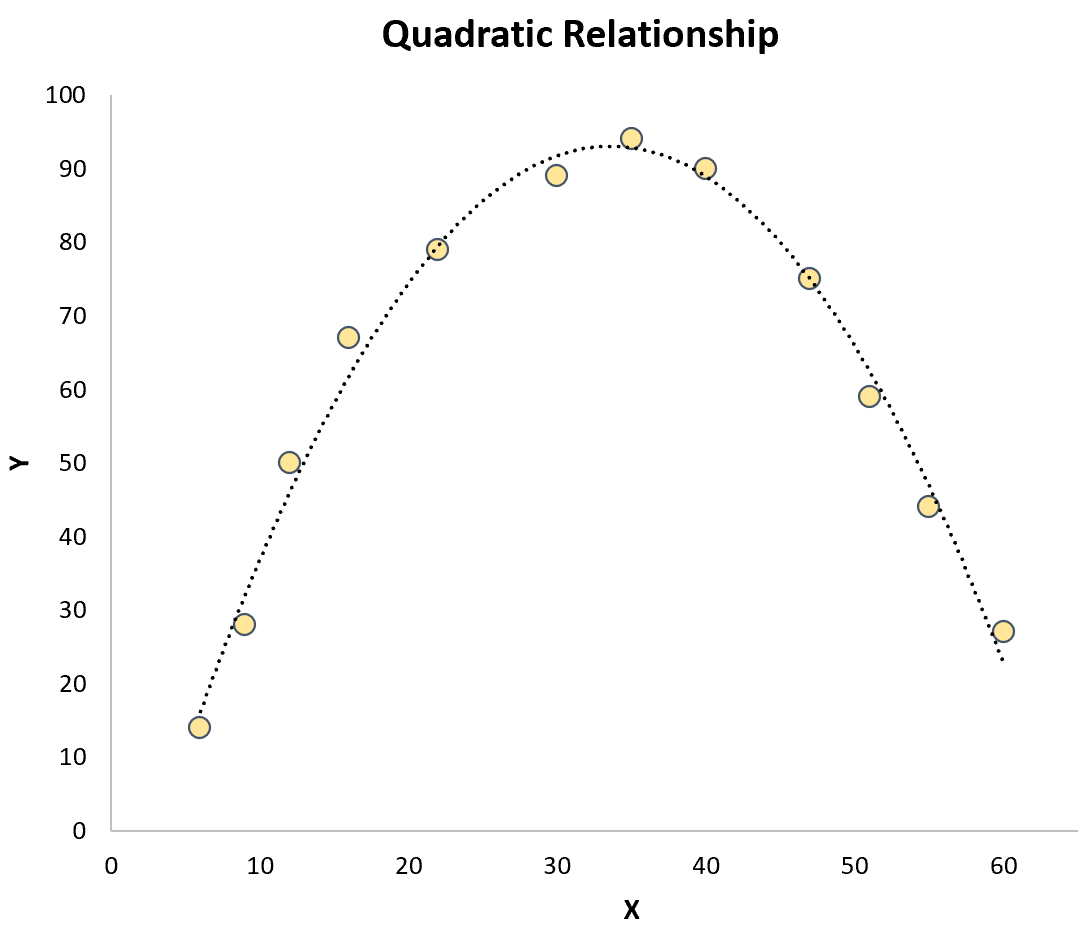
Kubische Regression: Wird verwendet, wenn eine kubische Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen besteht. In der grafischen Darstellung zeigt diese Art von Beziehung zwei unterschiedliche Kurven in einem Streudiagramm:

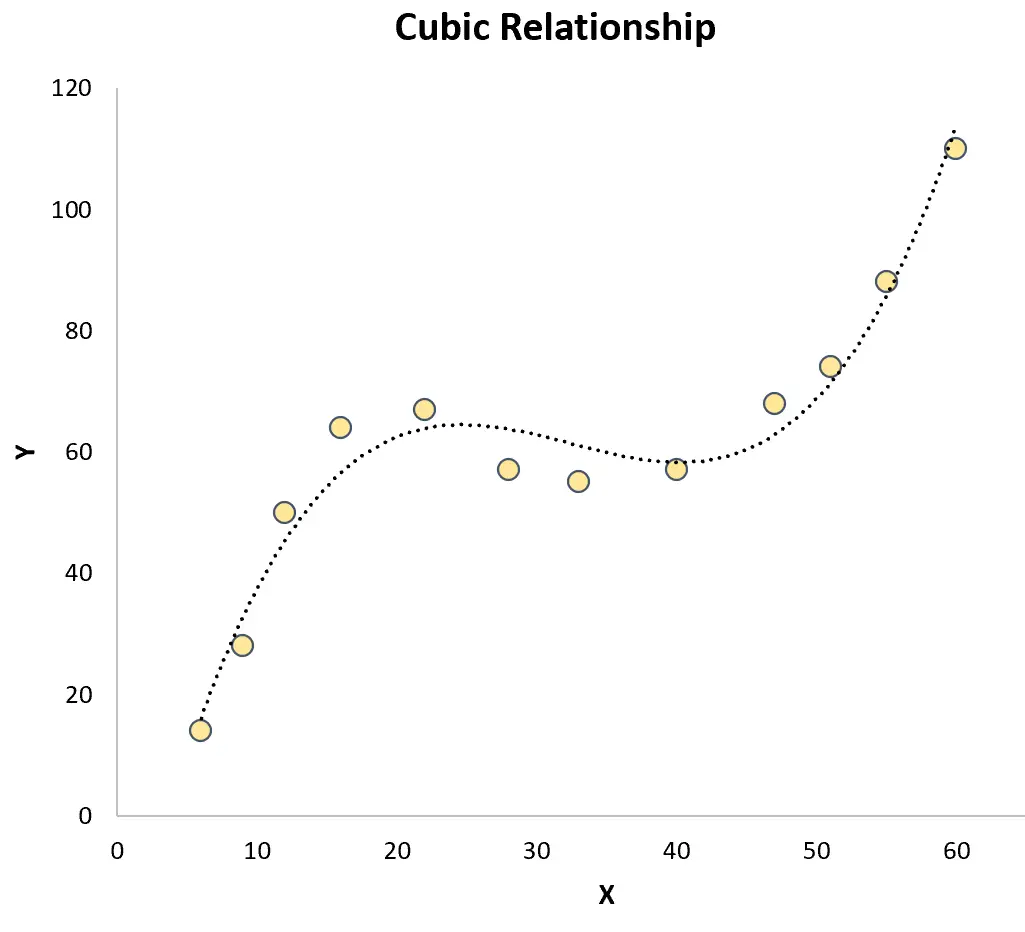
Beides steht im Gegensatz zur einfachen linearen Regression , bei der die Beziehung zwischen der Prädiktorvariablen und der Antwortvariablen linear ist:

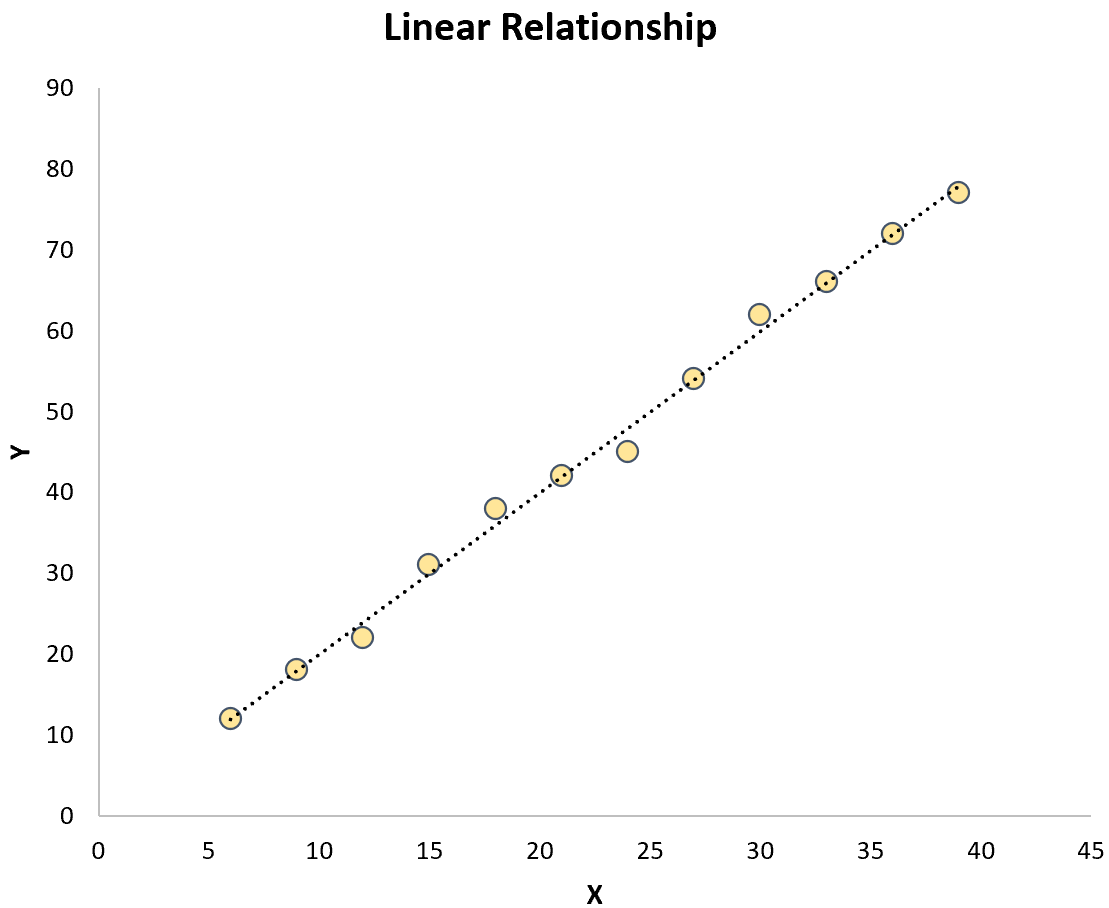
Die Formel für krummlinige Regressionsmodelle

Ein einfaches lineares Regressionsmodell versucht, einen Datensatz mithilfe der folgenden Formel anzupassen:

ŷ = β ₀ + β ₁ x

Gold:

• ŷ: Die Antwortvariable
• β ₀ , β ₁ : Die Regressionskoeffizienten
• x: die Vorhersagevariable

Im Gegensatz dazu verwendet ein quadratisches Regressionsmodell die folgende Formel:

ŷ = β ₀ + β ₁ x + β ₂ x ²

Und ein kubisches Regressionsmodell verwendet die folgende Formel:

ŷ = β ₀ + β ₁ x + β ₂ x ² + β ₃ x ³

Ein allgemeinerer Name für Regressionsmodelle, die Exponenten enthalten, ist Polynomregression , die die folgende Formel verwendet:

ŷ = β ₀ + β ₁ x + β ₂ x ² + … + β _k x ^k

Der Wert von k gibt den Grad des Polynoms an. Obwohl der Grad eine beliebige positive Zahl sein kann, passen wir in der Praxis selten polynomiale Regressionsmodelle mit einem Grad größer als 3 oder 4 an.

Durch die Verwendung von Exponenten in der Regressionsmodellformel können polynomiale Regressionsmodelle Kurven anstelle von geraden Linien an Datensätze anpassen.

Wann sollte die krummlinige Regression verwendet werden?

Der einfachste Weg herauszufinden, ob Sie die krummlinige Regression verwenden sollten oder nicht, besteht darin, ein Streudiagramm der Prädiktorvariablen und der Antwortvariablen zu erstellen.

Wenn das Streudiagramm eine lineare Beziehung zwischen den beiden Variablen zeigt, ist wahrscheinlich eine einfache lineare Regression angebracht.

Wenn das Streudiagramm jedoch ein quadratisches, kubisches oder anderes krummliniges Muster zwischen dem Prädiktor und der Antwortvariablen zeigt, ist die Verwendung einer krummlinigen Regression wahrscheinlich besser geeignet.

Sie können auch ein einfaches lineares Regressionsmodell und ein krummliniges Regressionsmodell anpassen und die angepassten R-Quadrat-Werte jedes Modells vergleichen, um zu bestimmen, welches Modell die beste Anpassung an die Daten bietet.

Das angepasste R-Quadrat ist nützlich, da es Ihnen sagt, wie viel der Varianz in der Antwortvariablen durch die Prädiktorvariablen erklärt werden kann, angepasst an die Anzahl der Prädiktorvariablen im Modell.

Im Allgemeinen bietet das Modell mit dem höchsten angepassten R-Quadrat-Wert eine bessere Anpassung an den Datensatz.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie eine Polynomregression in verschiedenen Statistikprogrammen durchführen:

Eine Einführung in die Polynomregression
So führen Sie eine Polynomregression in Excel durch
So führen Sie eine Polynomregression in Python durch
So führen Sie eine Polynomregression in R durch