So führen sie einen kruskal-wallis-test in excel durch

Mithilfe eines Kruskal-Wallis-Tests wird ermittelt, ob ein statistisch signifikanter Unterschied zwischen den Medianwerten von drei oder mehr unabhängigen Gruppen besteht. Sie gilt als nichtparametrisches Äquivalent der einfaktoriellen ANOVA.

In diesem Tutorial wird erläutert, wie Sie einen Kruskal-Wallis-Test in Excel durchführen.

Beispiel: Kruskal-Wallis-Test in Excel

Forscher wollen wissen, ob drei verschiedene Düngemittel zu unterschiedlichem Pflanzenwachstum führen. Sie wählen nach dem Zufallsprinzip 30 verschiedene Pflanzen aus und teilen sie in drei Gruppen zu je zehn Pflanzen auf, wobei sie jeder Gruppe einen anderen Dünger hinzufügen. Nach einem Monat messen sie die Höhe jeder Pflanze.

Befolgen Sie die folgenden Schritte, um einen Kruskal-Wallis-Test durchzuführen und festzustellen, ob das mittlere Wachstum in allen drei Gruppen gleich ist.

Schritt 1: Geben Sie die Daten ein.

Geben Sie die folgenden Daten ein, die das Gesamtwachstum (in Zoll) jeder der 10 Pflanzen in jeder Gruppe zeigen:

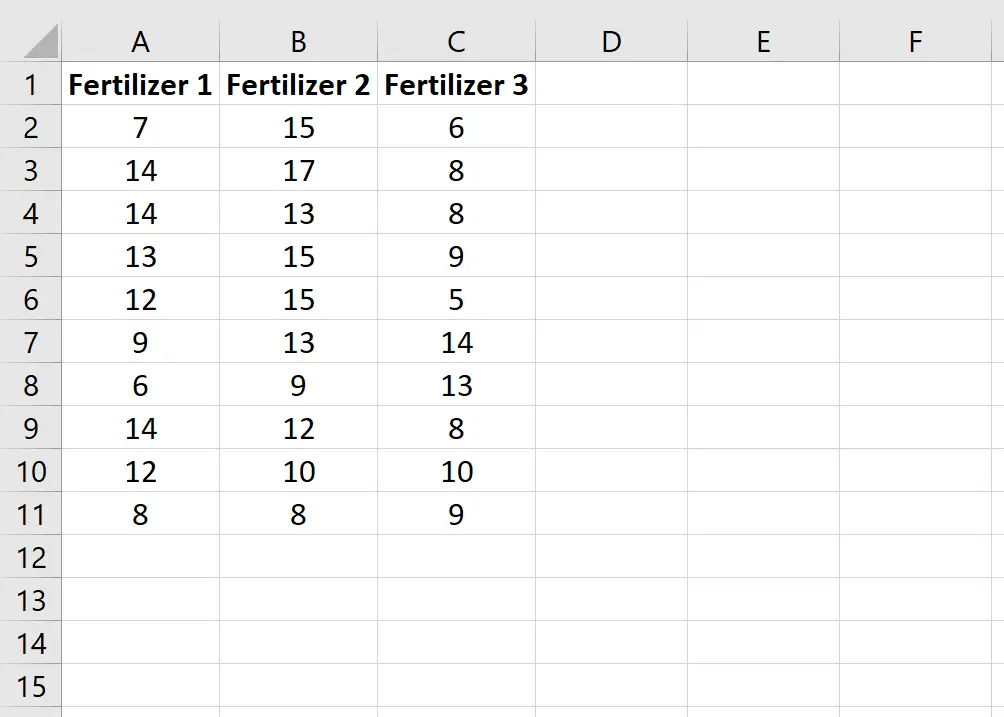
Schritt 2: Klassifizieren Sie die Daten.

Als nächstes verwenden wir die Funktion RANK.AVG() , um dem Wachstum jeder Pflanze unter den 30 Pflanzen einen Rang zuzuweisen. Die folgende Formel zeigt, wie der Rang der ersten Pflanze in der ersten Gruppe berechnet wird:

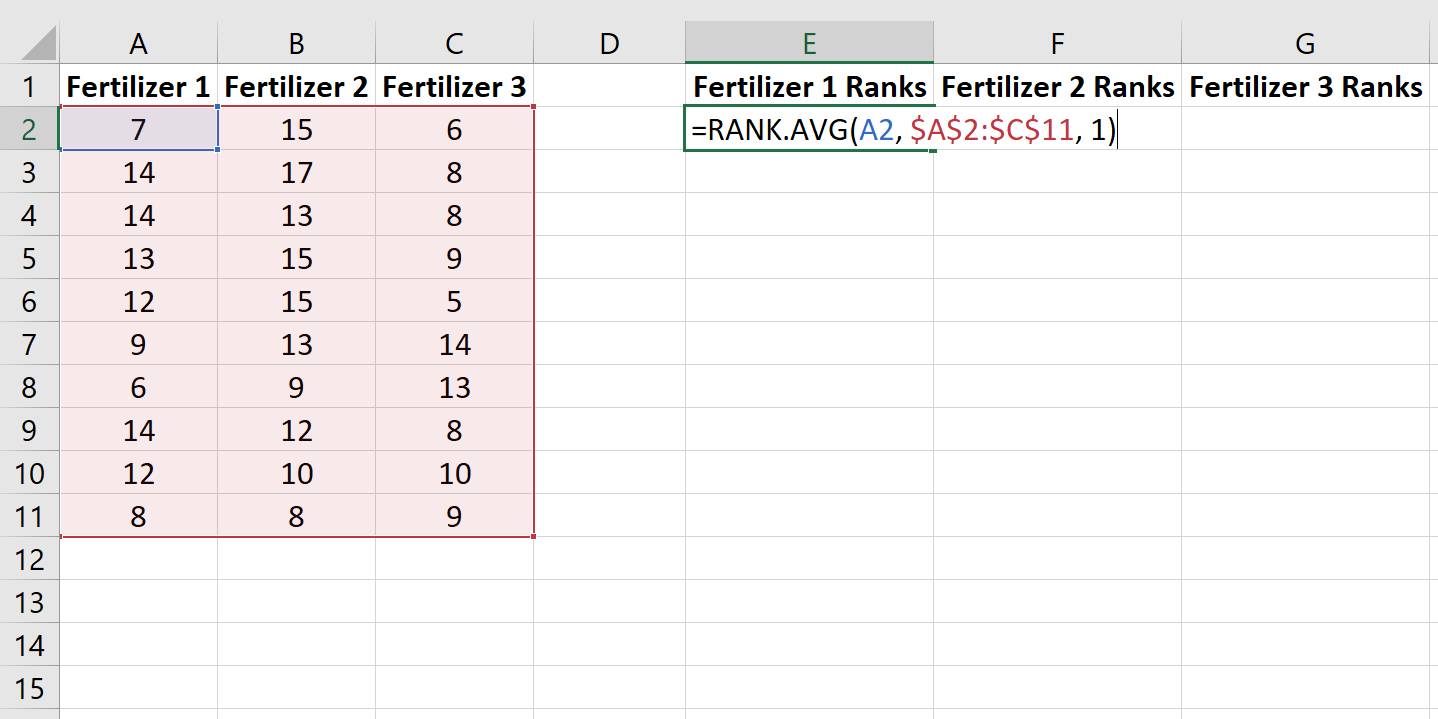
Kopieren Sie diese Formel in die restlichen Zellen:

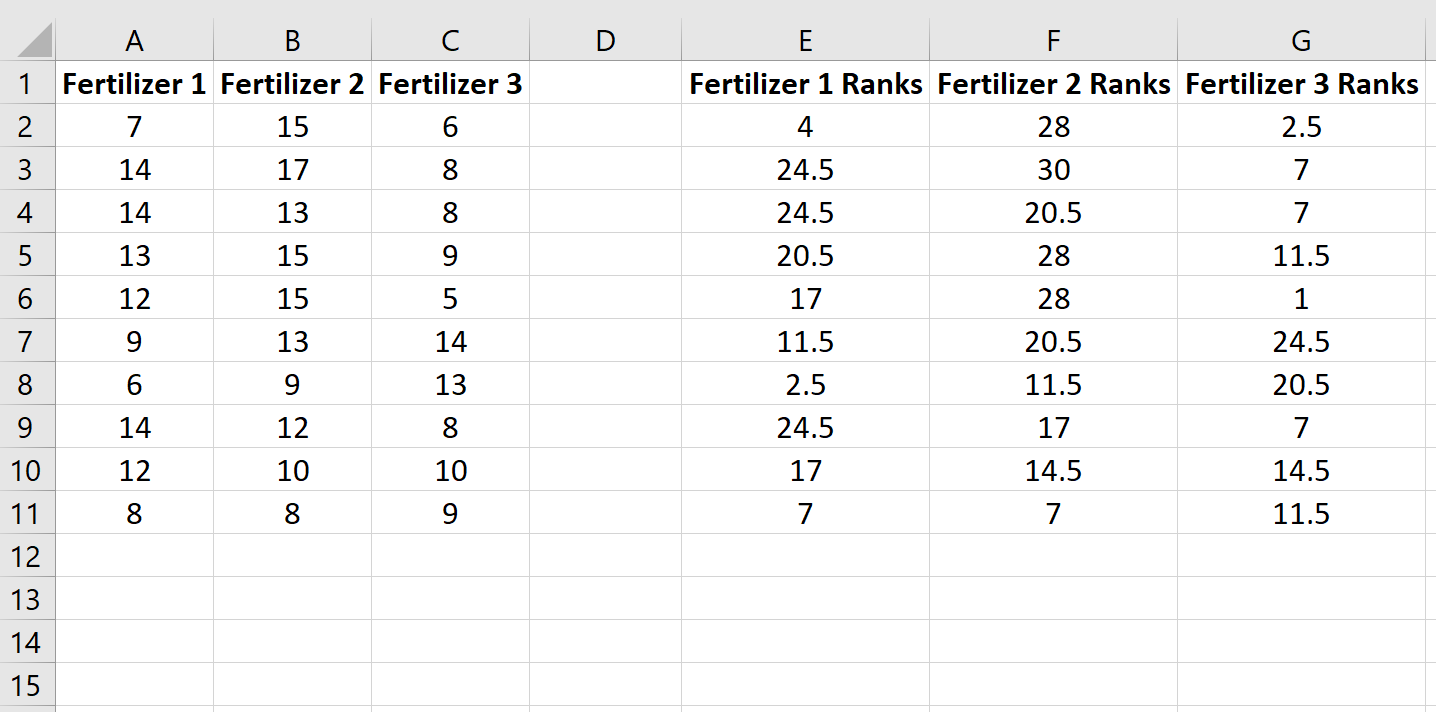
Berechnen Sie als Nächstes die Summe der Ränge für jede Spalte zusammen mit der Stichprobengröße und der quadrierten Summe der Ränge dividiert durch die Stichprobengröße:

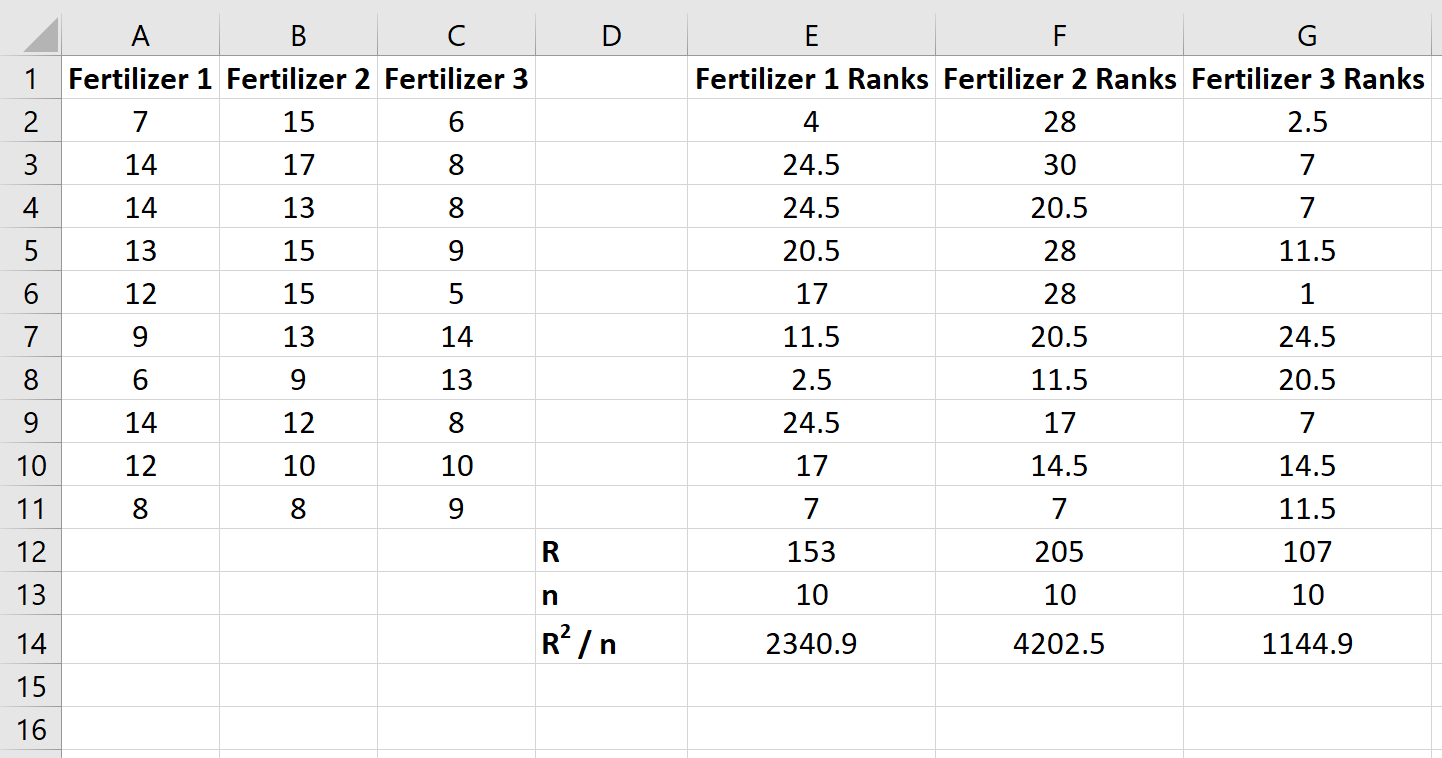
Schritt 3: Berechnen Sie die Teststatistik und den entsprechenden p-Wert.

Die Teststatistik ist definiert als:

H = 12/(n(n+1)) * ΣR _j ² /n _j – 3(n+1)

Gold:

• n = Gesamtstichprobengröße
• R _j ² = Summe der Ränge für die ^j-te Gruppe
• n _j = Stichprobengröße der ^j-ten Gruppe

Unter der Nullhypothese folgt H einer Chi-Quadrat-Verteilung mit k-1 Freiheitsgraden.

Der folgende Screenshot zeigt die Formeln zur Berechnung der Teststatistik H und des entsprechenden p-Werts:

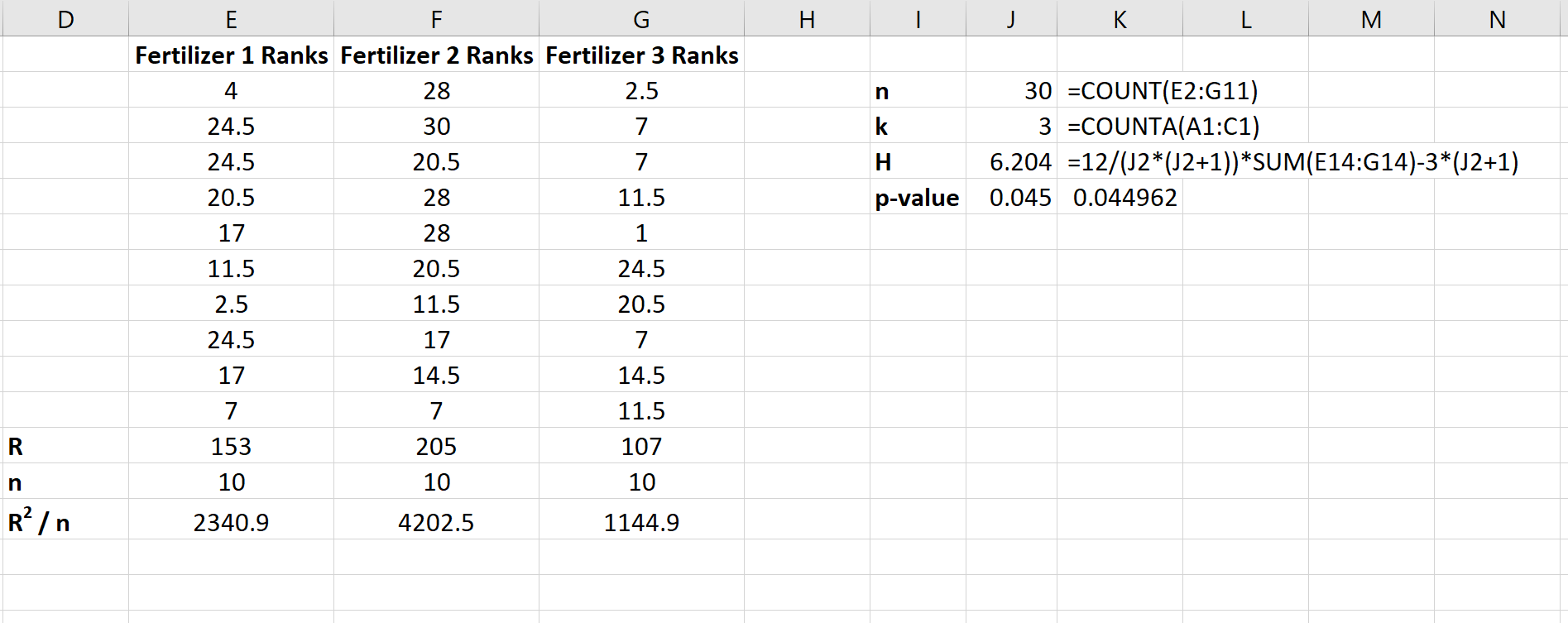
Die Teststatistik ist H = 6,204 und der entsprechende p-Wert ist p = 0,045 . Da dieser p-Wert kleiner als 0,05 ist, können wir die Nullhypothese zurückweisen, dass das mittlere Pflanzenwachstum für alle drei Düngemittel gleich ist. Wir haben genügend Beweise, um zu dem Schluss zu kommen, dass die Art des verwendeten Düngers statistisch signifikante Unterschiede im Pflanzenwachstum verursacht.

Schritt 4: Melden Sie die Ergebnisse.

Abschließend möchten wir über die Ergebnisse des Kruskal-Wallis-Tests berichten. Hier ist ein Beispiel dafür:

Ein Kruskal-Wallist-Test wurde durchgeführt, um festzustellen, ob das mittlere Pflanzenwachstum bei drei verschiedenen Pflanzendüngern gleich war. Insgesamt wurden 30 Pflanzen für die Analyse verwendet. Jeder Dünger wurde auf 10 verschiedene Pflanzen ausgebracht.

Der Test ergab, dass das mittlere Pflanzenwachstum zwischen den drei Düngemitteln nicht gleich war (H = 6,204, p = 0,045). Das heißt, es gab einen statistisch signifikanten Unterschied im mittleren Pflanzenwachstum zwischen zwei oder mehr Düngemitteln.