So führen sie einen kruskal-wallis-test in spss durch

Mithilfe eines Kruskal-Wallis-Tests wird ermittelt, ob ein statistisch signifikanter Unterschied zwischen den Medianwerten von drei oder mehr unabhängigen Gruppen besteht. Sie gilt als nichtparametrisches Äquivalent der einfaktoriellen ANOVA .

In diesem Tutorial wird erläutert, wie Sie einen Kruskal-Wallis-Test in SPSS durchführen.

Beispiel: Kruskal-Wallis-Test in SPSS

Ein Forscher möchte wissen, ob drei Medikamente unterschiedliche Wirkungen auf Knieschmerzen haben. Deshalb rekrutiert er 30 Personen, die alle unter ähnlichen Knieschmerzen leiden, und teilt sie nach dem Zufallsprinzip in drei Gruppen ein, um entweder Medikament 1, Medikament 2 oder Medikament 3 zu erhalten.

Nach einem Monat Einnahme des Medikaments bittet der Forscher jeden Einzelnen, seine Knieschmerzen auf einer Skala von 1 bis 100 einzuschätzen, wobei 100 den stärksten Schmerz angibt. Nachfolgend werden die Ergebnisse der 30 Personen dargestellt:

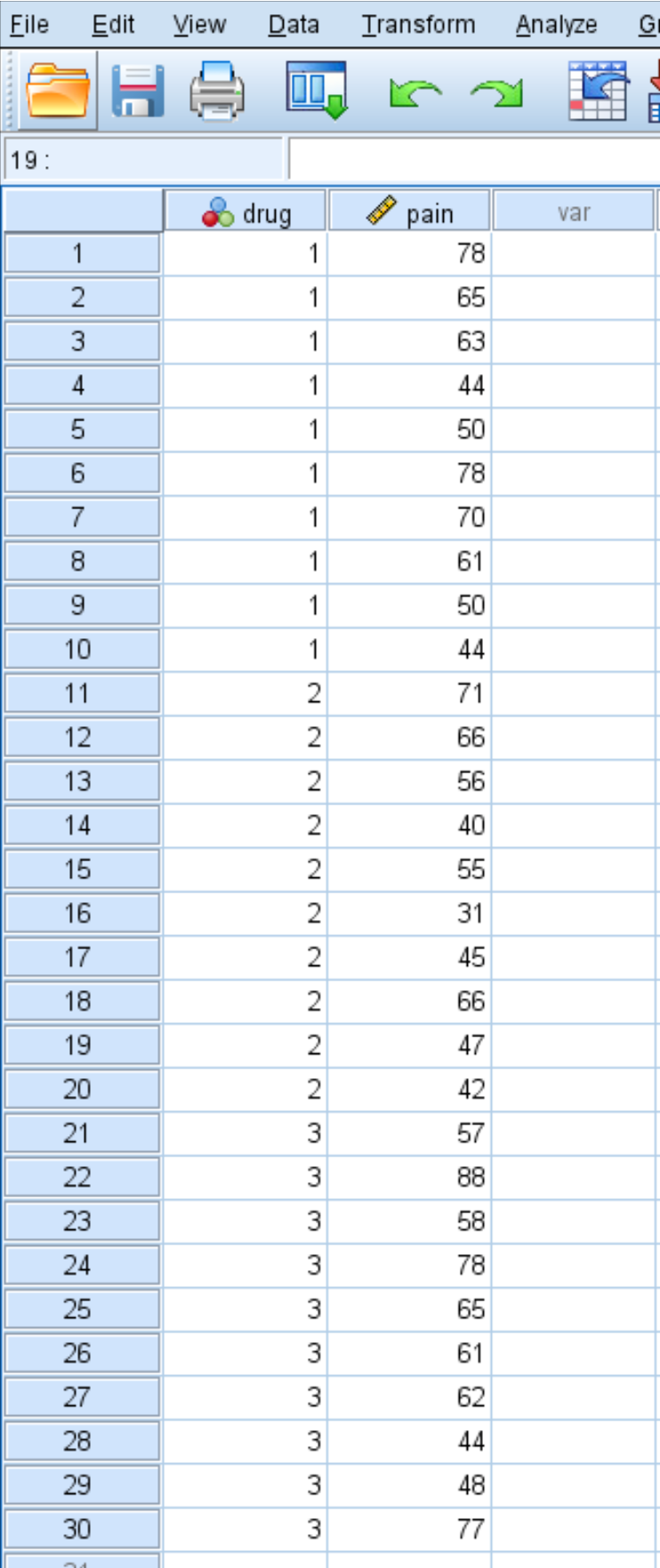
Befolgen Sie die folgenden Schritte, um einen Kruskal-Wallis-Test durchzuführen und festzustellen, ob zwischen den drei Gruppen ein Unterschied bei den gemeldeten Knieschmerzniveaus besteht:

Schritt 1: Führen Sie einen Kruskal-Wallis-Test durch.

Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Nichtparametrische Tests“ , dann auf „Legacy Dialogs“ und dann auf „K Independent Samples“ :

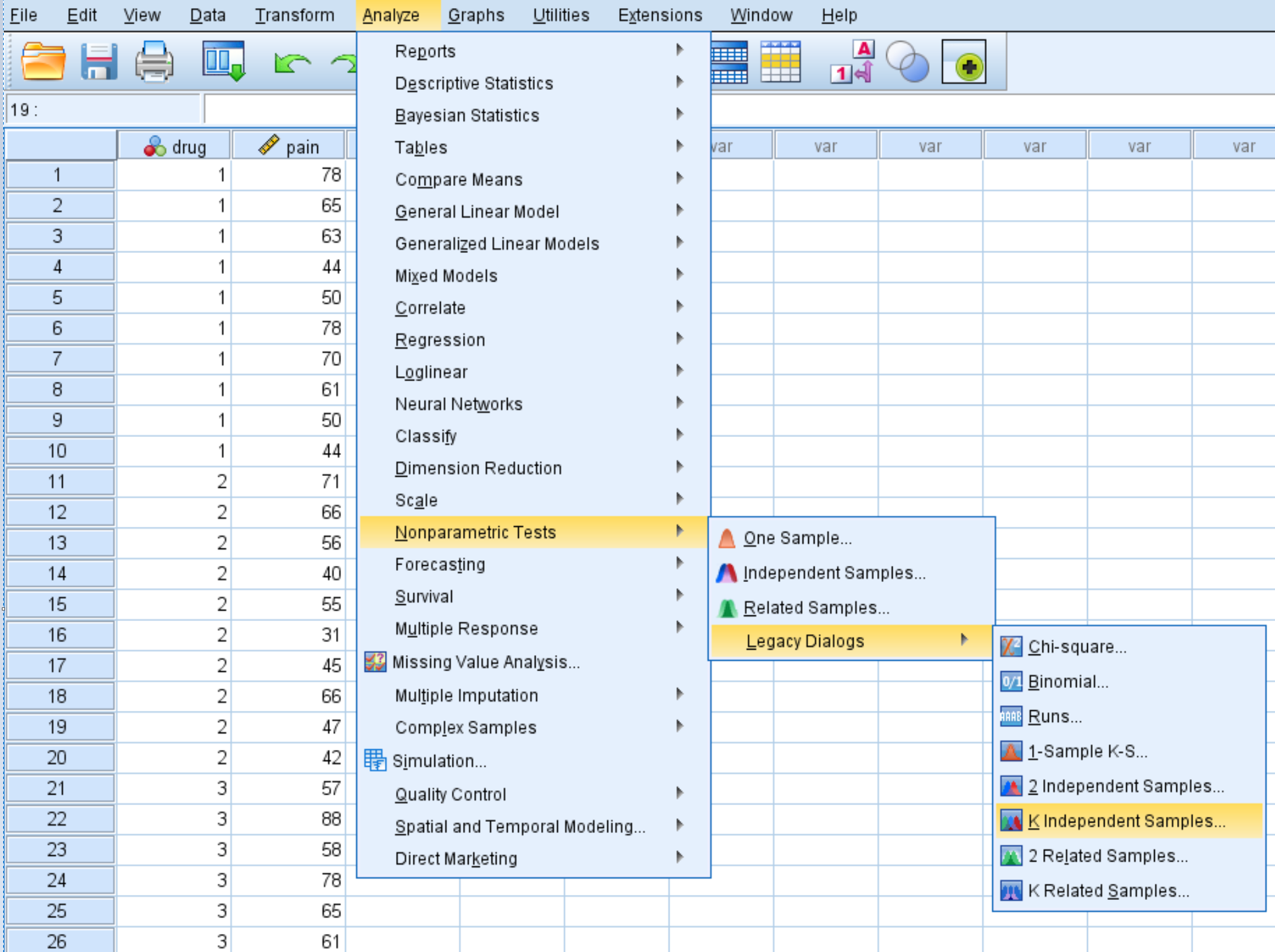
Ziehen Sie im angezeigten Fenster die Schmerzvariable in das Feld mit der Bezeichnung „Liste der Testvariablen“ und das Medikament in das Feld mit der Bezeichnung „Gruppierungsvariable“. Klicken Sie dann auf „Bereich festlegen“ und legen Sie den Mindestwert auf 1 und den Höchstwert auf 3 fest. Klicken Sie dann auf „Weiter“ . Stellen Sie sicher, dass das Kontrollkästchen neben Kruskal-Wallis H aktiviert ist, und klicken Sie dann auf OK .

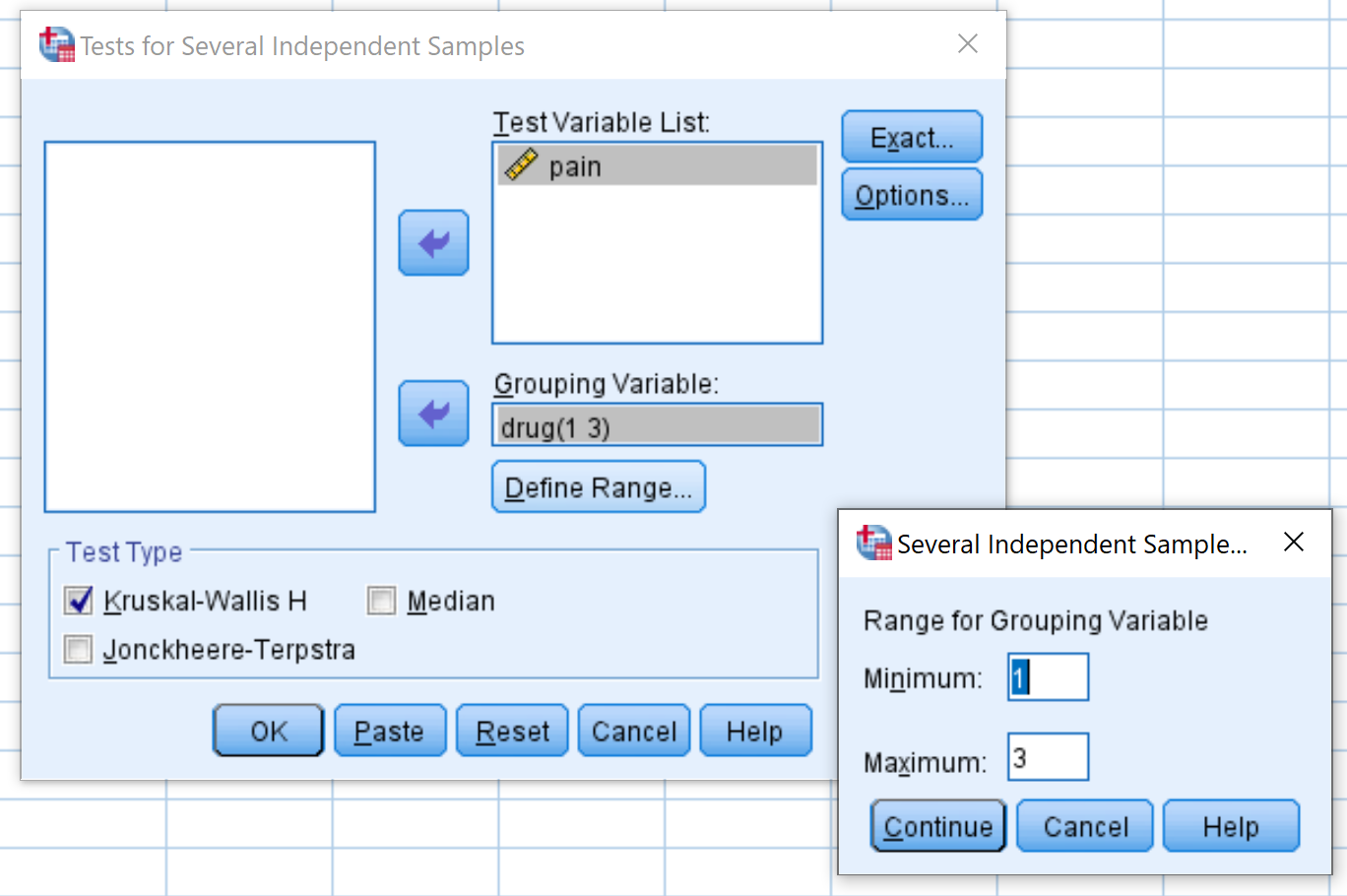
Schritt 2: Interpretieren Sie die Ergebnisse.

Sobald Sie auf „OK“ klicken, werden die Ergebnisse des Kruskal-Wallis-Tests angezeigt:

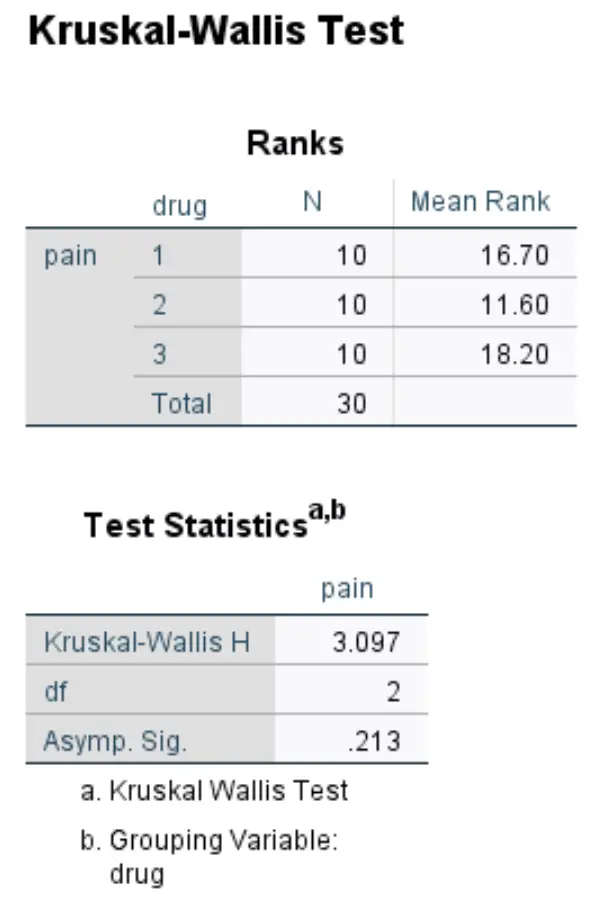
Die zweite Tabelle in der Ausgabe zeigt die Testergebnisse:

• Kruskal-Wallis H: Das ist die X ^2- Teststatistik.
• df: Dies sind die Freiheitsgrade, berechnet als #Gruppen-1 = 3-1 = 2.
• Asymp. Sig: Dies ist der p-Wert, der einer ^X2- Teststatistik von 3,097 mit 2 Freiheitsgraden zugeordnet ist. Dies kann auch mit dem Chi-Quadrat-Score-zu-P-Wert-Rechner ermittelt werden.

Da der p-Wert (0,213) nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen. Wir haben keine ausreichenden Belege dafür, dass zwischen diesen drei Gruppen ein statistisch signifikanter Unterschied in der Bewertung von Knieschmerzen besteht.