So führen sie einen kruskal-wallis-test in stata durch

Mithilfe eines Kruskal-Wallis-Tests wird ermittelt, ob ein statistisch signifikanter Unterschied zwischen den Medianwerten von drei oder mehr unabhängigen Gruppen besteht. Sie gilt als nichtparametrisches Äquivalent der einfaktoriellen ANOVA .

In diesem Tutorial wird erläutert, wie Sie einen Kruskal-Wallis-Test in Stata durchführen.

So führen Sie einen Kruskal-Wallis-Test in Stata durch

Für dieses Beispiel verwenden wir den Zensus- Datensatz, der Volkszählungsdaten von 1980 für alle fünfzig Bundesstaaten der Vereinigten Staaten enthält. Im Datensatz werden Staaten in vier verschiedene Regionen kategorisiert:

• Nord Est
• Nord-Zentral
• Süd
• Westen

Wir werden einen Kruskal-Wallis-Test durchführen, um festzustellen, ob das Durchschnittsalter in diesen vier Regionen gleich ist.

Schritt 1: Daten laden und anzeigen.

Laden Sie zunächst den Datensatz, indem Sie den folgenden Befehl in das Befehlsfeld eingeben:

Verwenden Sie https://www.stata-press.com/data/r13/census

Erhalten Sie mit dem folgenden Befehl eine kurze Zusammenfassung des Datensatzes:

zusammenfassen

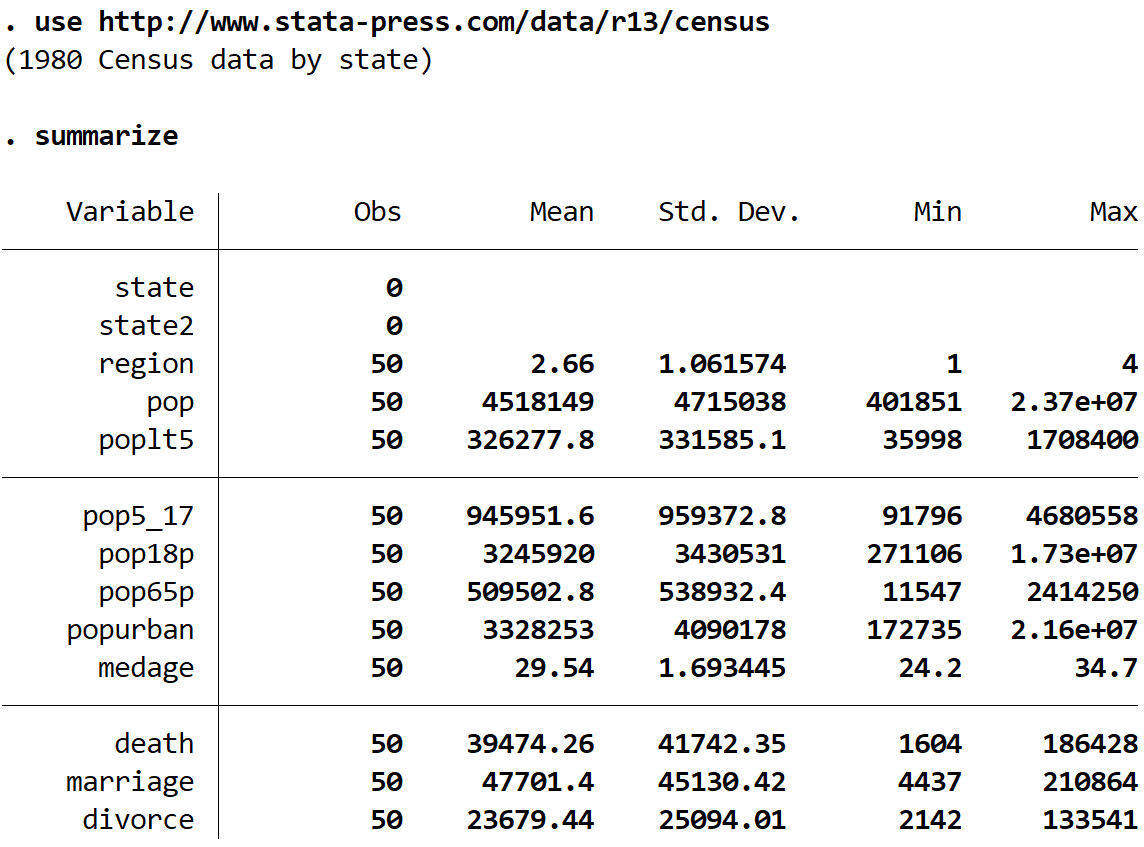
Wir können sehen, dass dieser Datensatz 13 verschiedene Variablen enthält, aber die einzigen zwei, mit denen wir arbeiten werden, sind Medage (Durchschnittsalter) und Region .

Schritt 2: Visualisieren Sie die Daten.

Bevor wir den Kruskal-Wallis-Test durchführen, erstellen wir zunächst einige Boxplots , um die mittlere Altersverteilung für jede der vier Regionen zu visualisieren:

Medage-Grafikbox, auf (Region)

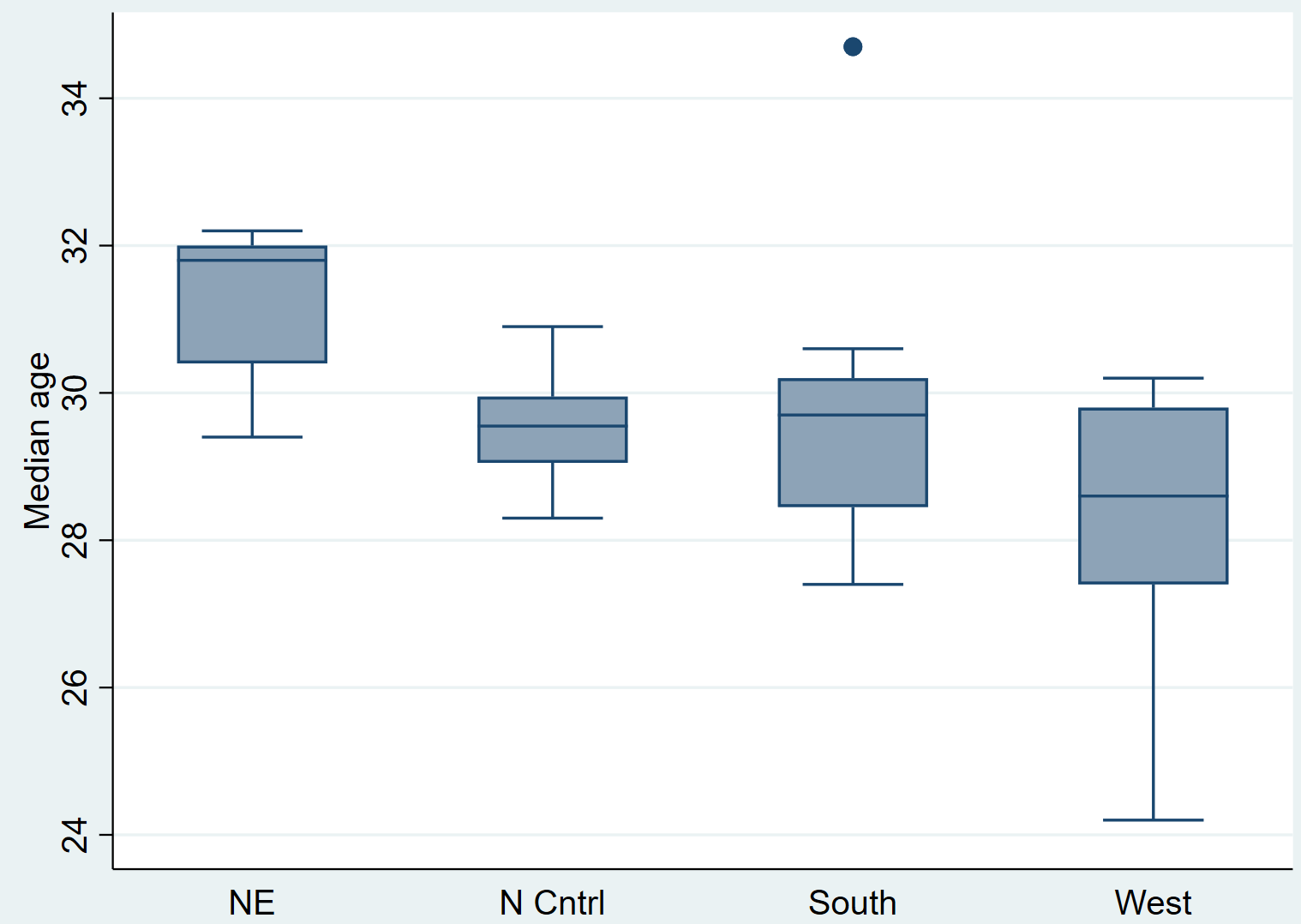
Wenn Sie sich nur die Boxplots ansehen, können Sie erkennen, dass die Verteilungen von Region zu Region unterschiedlich zu sein scheinen. Anschließend führen wir einen Kruskal-Wallis-Test durch, um festzustellen, ob diese Unterschiede statistisch signifikant sind.

Schritt 3: Führen Sie einen Kruskal-Wallis-Test durch.

Verwenden Sie die folgende Syntax, um einen Kruskal-Wallis-Test durchzuführen:

kwalis Measure_variable, by (grouping_variable)

In unserem Fall verwenden wir die folgende Syntax:

Kwallis Medage, von (Region)

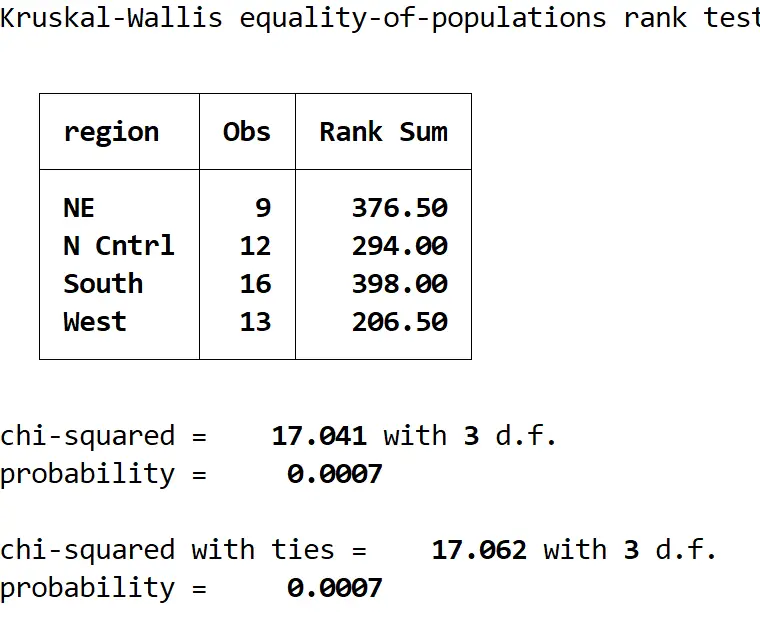
So interpretieren Sie das Ergebnis:

Übersichtstabelle: Diese Tabelle zeigt die Anzahl der Beobachtungen pro Region und die Rangfolgesummen für jede Region.

Chi-Quadrat mit Bindungen: Dies ist der Wert der Teststatistik, der sich als 17,062 herausstellt.

Wahrscheinlichkeit: Dies ist der p-Wert, der der Teststatistik entspricht, die sich als 0,0007 herausstellt. Da dieser Wert kleiner als 0,05 ist, können wir die Nullhypothese ablehnen und daraus schließen, dass das Durchschnittsalter in den vier Regionen nicht gleich ist.

Schritt 4: Melden Sie die Ergebnisse.

Abschließend möchten wir über die Ergebnisse des Kruskal-Wallis-Tests berichten. Hier ist ein Beispiel dafür:

Ein Kruskal-Wallist-Test wurde durchgeführt, um festzustellen, ob das Durchschnittsalter der Personen in den folgenden vier Regionen der Vereinigten Staaten gleich war:

• Nordosten (n=9)
• Nord-Zentral (n=12)
• Süden (n=16)
• Westen (n=13)

Der Test ergab, dass das Durchschnittsalter der Personen in den vier Regionen nicht gleich war (X ² = 17,062, p = 0,0007). Das heißt, es gab einen statistisch signifikanten Unterschied im Durchschnittsalter zwischen zwei oder mehr Regionen.