Kumulierte relative häufigkeit

In diesem Artikel wird erläutert, was die kumulative relative Häufigkeit in der Statistik ist. Sie finden also die Definition der kumulativen relativen Häufigkeit, wie man die kumulative relative Häufigkeit ermittelt und zwei Übungen, die Schritt für Schritt gelöst werden.

Was ist die kumulative relative Häufigkeit?

In der Statistik ist die kumulative relative Häufigkeit die kumulative Summe der relativen Häufigkeiten. Das heißt, die kumulative relative Häufigkeit eines Werts ist gleich der relativen Häufigkeit dieses Werts plus der relativen Häufigkeit aller Werte, die kleiner als dieser sind.

Das Symbol für die kumulative relative Häufigkeit ist H _i . Allerdings besteht in der Statistik noch kein vollständiger Konsens über das Symbol für diese Art von Frequenz, weshalb es auch mit einem anderen Symbol ausgedrückt werden kann.

Um die Bedeutung der kumulativen relativen Häufigkeit zu verstehen, müssen Sie sich natürlich zunächst über das Konzept der relativen Häufigkeit im Klaren sein. Deshalb empfehle ich Ihnen, den folgenden Link zu besuchen, bevor Sie mit der Erklärung fortfahren:

So berechnen Sie die kumulative relative Häufigkeit

Um die kumulative relative Häufigkeit zu berechnen, müssen die folgenden Schritte befolgt werden:

1. Erstellen Sie eine Häufigkeitstabelle mit allen verschiedenen Werten aus der statistischen Stichprobe.
2. Berechnen Sie die absolute Häufigkeit jedes Werts.
3. Bestimmen Sie aus den absoluten Häufigkeiten die relative Häufigkeit jedes Werts.
4. Ermitteln Sie die kumulative relative Häufigkeit jedes Werts. Sie wird berechnet, indem Sie die relative Häufigkeit des Werts selbst plus die relativen Häufigkeiten aller kleineren Werte addieren.

Beachten Sie, dass Sie, wenn Sie den kumulativen relativen Häufigkeitsprozentsatz , also die kumulative relative Häufigkeit ausgedrückt als Prozentsatz, berechnen möchten, einfach die gleichen Schritte ausführen und die Ergebnisse mit 100 multiplizieren müssen.

Beispiele für kumulative relative Häufigkeit

Damit Sie sehen können, wie die kumulative relative Häufigkeit berechnet wird, sind im Folgenden zwei Beispiele aufgeführt, die Schritt für Schritt gelöst werden. Im ersten Beispiel finden wir die kumulative relative Häufigkeit einer diskreten Variablen und im zweiten Beispiel eine kontinuierliche Variable, da der Prozess leicht variiert.

Beispiel 1: diskrete Variable

• Die im Fach Statistik in einer Klasse mit 30 Schülern erzielten Noten lauten wie folgt. Wie hoch ist die kumulative relative Häufigkeit jeder Note?

In diesem Fall ist die Variable diskret, da sie keinen Dezimalwert annehmen kann. Es ist daher nicht notwendig, die Daten nach Intervallen zu gruppieren, sondern die Berechnungen können direkt durchgeführt werden.

Also erstellen wir eine Häufigkeitstabelle und bestimmen die absolute Häufigkeit jedes einzelnen Wertes:

Als nächstes berechnen wir die relative Häufigkeit jedes Werts (wie das geht, können Sie im Link am Anfang des Beitrags sehen).

Und sobald wir die absolute Häufigkeit und die relative Häufigkeit des Datensatzes berechnet haben, können wir die kumulative relative Häufigkeit ermitteln. Dazu müssen wir die relative Häufigkeit des betreffenden Wertes plus alle vorherigen relativen Häufigkeiten oder, anders ausgedrückt, die bisherige kumulierte relative Häufigkeit addieren:

Kurz gesagt, die Häufigkeitstabelle mit absoluter Häufigkeit, relativer Häufigkeit und kumulativer relativer Häufigkeit lautet wie folgt:

Beachten Sie, dass der letzte Wert der kumulativen relativen Häufigkeit immer 1 sein sollte. Wenn Sie eine andere Zahl erhalten, bedeutet dies, dass Sie bei den Berechnungen einen Fehler gemacht haben.

Beispiel 2: kontinuierliche Variable

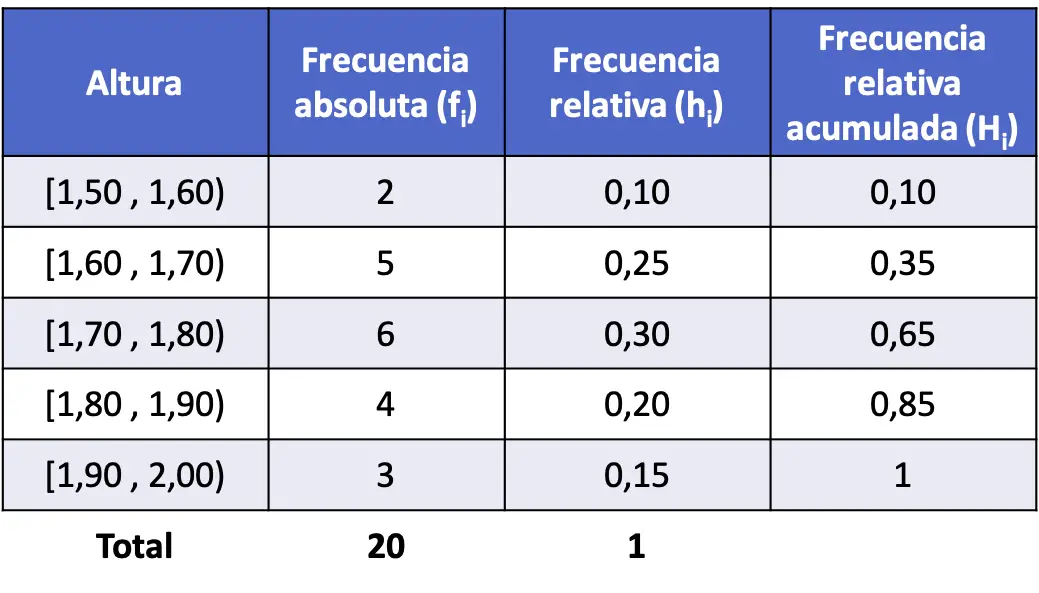
• Die Körpergröße von 20 Personen wurde gemessen und die unten aufgeführten Ergebnisse erzielt. Teilen Sie die Daten in Intervalle auf und ermitteln Sie die kumulative relative Häufigkeit jedes Intervalls.

Dieser Fall unterscheidet sich vom vorherigen Problem, da die Zahlen dezimal sind, was bedeutet, dass die Variable jeden Wert annehmen kann und daher stetig ist. Wir erstellen daher die Häufigkeitstabelle, indem wir die Daten in Intervalle gruppieren.

Wir erstellen daher die Tabelle und erhalten die absolute Häufigkeit jedes Intervalls:

Wir berechnen nun die relativen Häufigkeiten, indem wir die absolute Häufigkeit jedes Intervalls durch die Gesamtzahl der Datenpunkte dividieren:

Und schließlich finden wir die kumulativen relativen Häufigkeiten aller Intervalle. Um eine kumulative relative Häufigkeit eines Intervalls zu bestimmen, ist es wie zuvor notwendig, die relative Häufigkeit dieses Intervalls plus die vorherigen relativen Häufigkeiten zu addieren:

Kumulierte relative Häufigkeit und kumulative absolute Häufigkeit

Wir haben gerade gesehen, wie die kumulative relative Häufigkeit aus der relativen Häufigkeit abgeleitet wird. Diese Art von Häufigkeit kann jedoch auch anhand der kumulierten absoluten Häufigkeit ermittelt werden.

Die kumulative relative Häufigkeit kann berechnet werden, indem die kumulative absolute Häufigkeit durch die Gesamtzahl der Daten in der Stichprobe dividiert wird.

Daher lautet die Formel für die kumulative relative Häufigkeit :

Gold:

• 

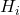
  ist die kumulative relative Häufigkeit.

• 

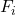
  ist die akkumulierte absolute Häufigkeit .

• 

  ist die Gesamtzahl der Daten.

In Anlehnung an das erste oben entwickelte Beispiel wird hier die akkumulierte relative Häufigkeit aus der akkumulierten absoluten Häufigkeit ermittelt:

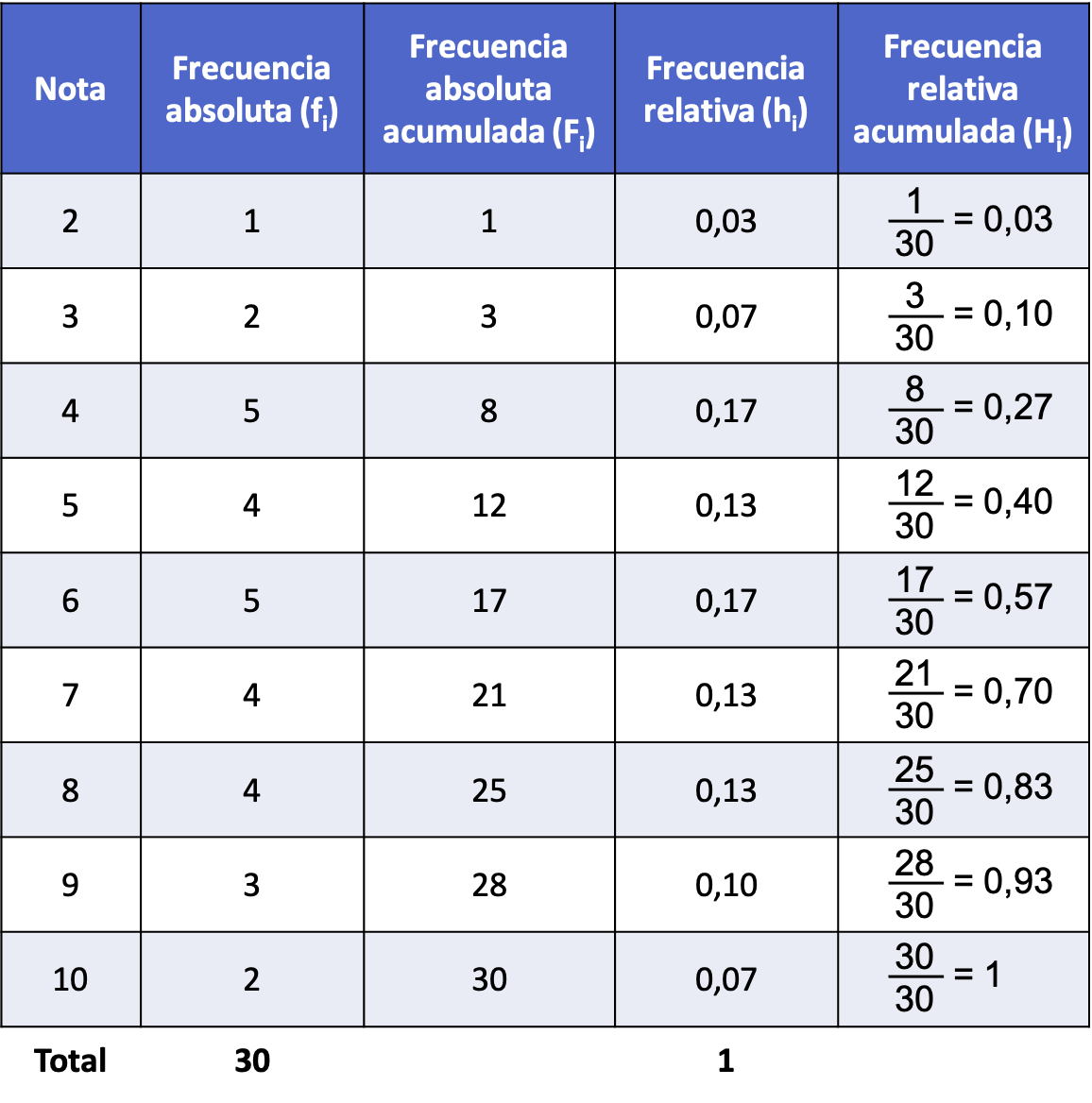
Die obige Tabelle wird als Häufigkeitstabelle bezeichnet, da sie alle Arten statistischer Häufigkeiten enthält. Klicken Sie hier, um mehr zu erfahren: