Kurvenanpassung in excel (mit beispielen)

Häufig möchten Sie möglicherweise die Gleichung finden, die am besten zu einer Kurve für einen Datensatz in Excel passt.

Glücklicherweise ist dies mit der Trendlinienfunktion von Excel recht einfach zu bewerkstelligen.

Dieses Tutorial bietet ein schrittweises Beispiel für die Anpassung einer Gleichung an eine Kurve in Excel.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst einen gefälschten Datensatz, mit dem wir arbeiten können:

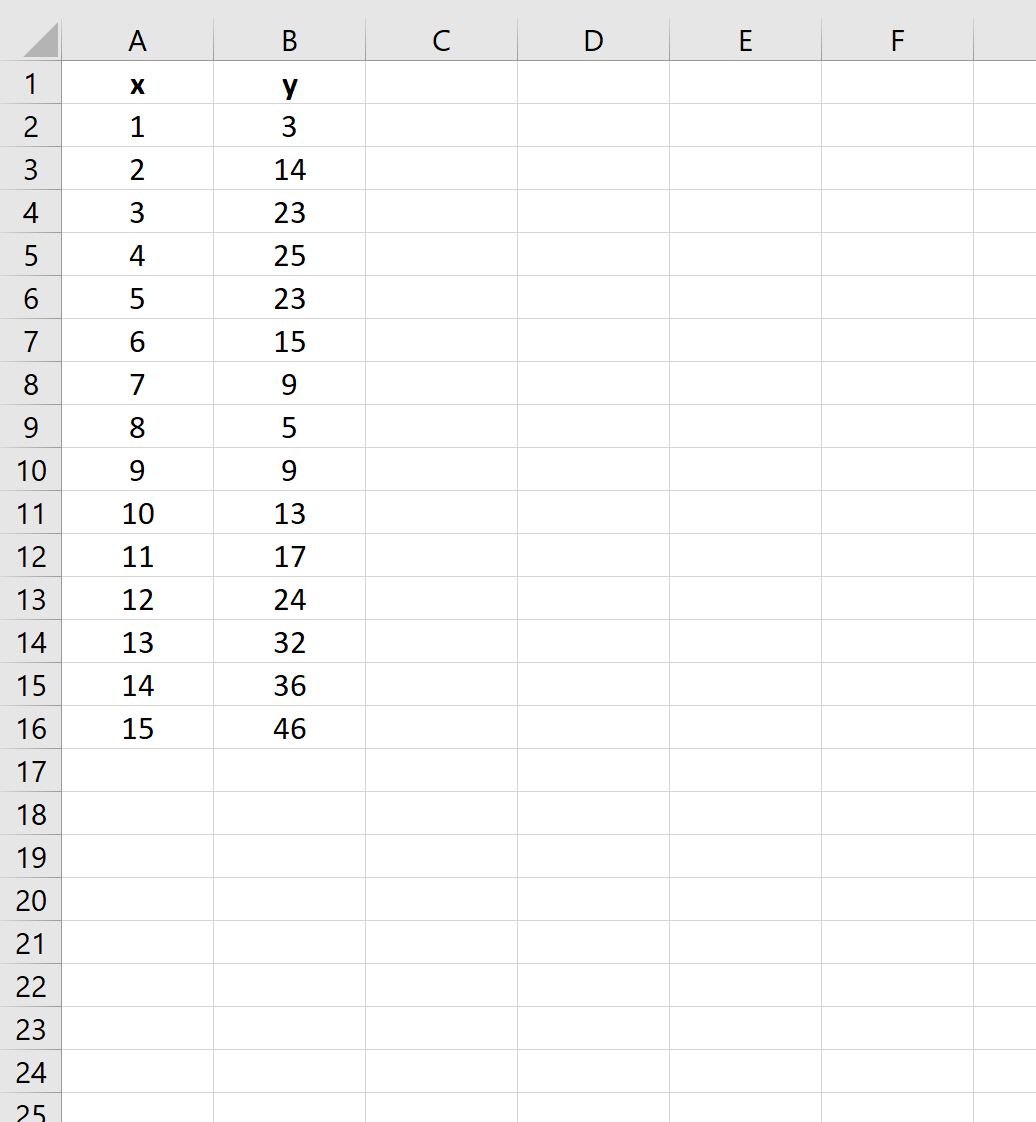
Schritt 2: Erstellen Sie ein Streudiagramm

Als Nächstes erstellen wir ein Streudiagramm, um den Datensatz zu visualisieren.

Markieren Sie zunächst die Zellen A2:B16 wie folgt:

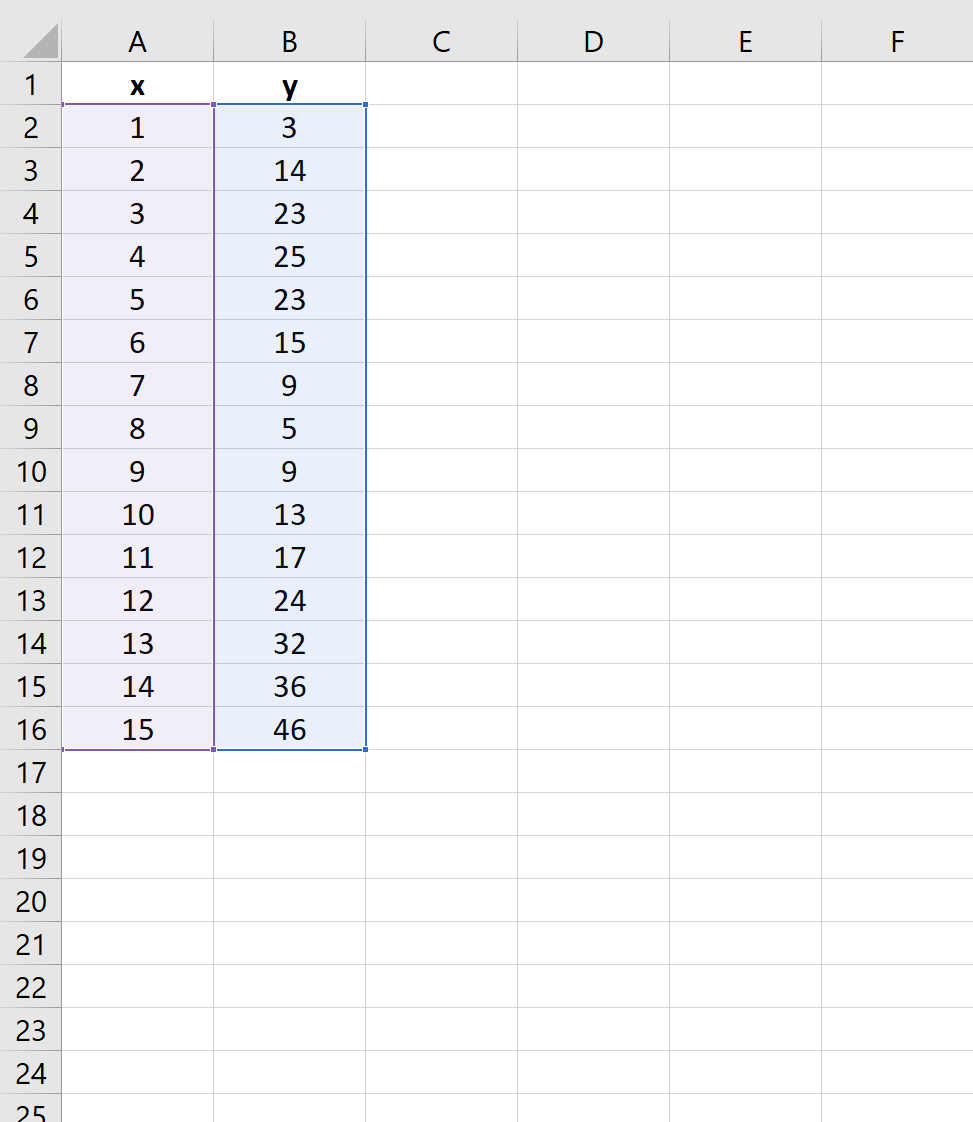
Klicken Sie anschließend im oberen Menüband auf die Registerkarte „Einfügen“ und dann auf die erste Plotoption unter „Streuung“ :

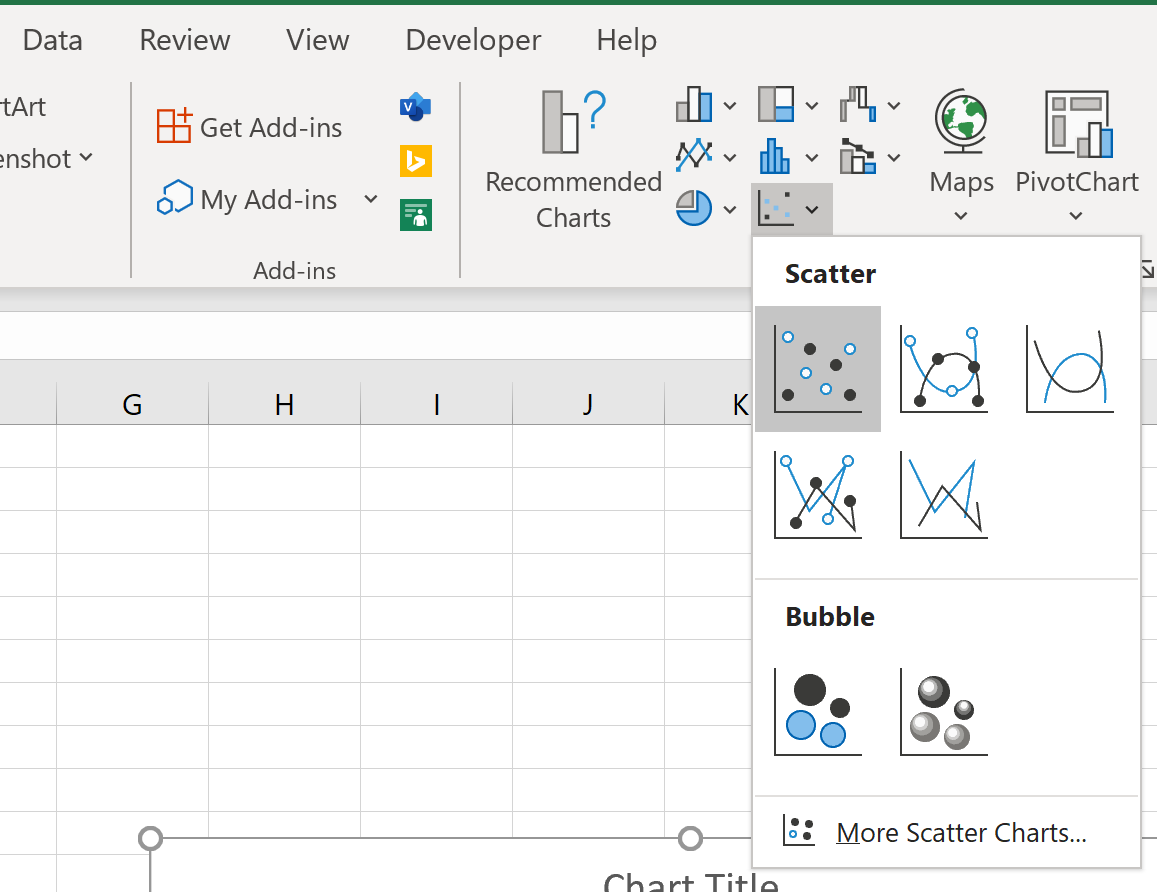
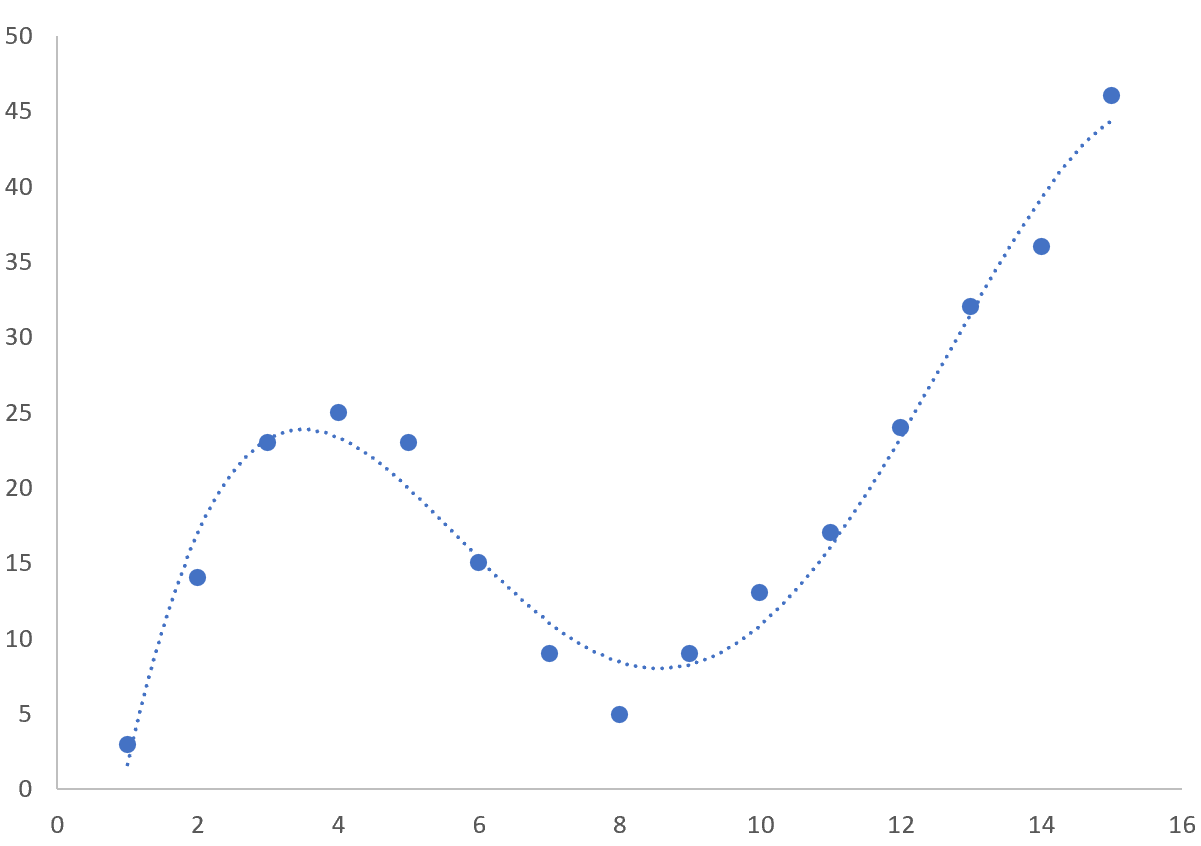
Dadurch entsteht das folgende Streudiagramm:

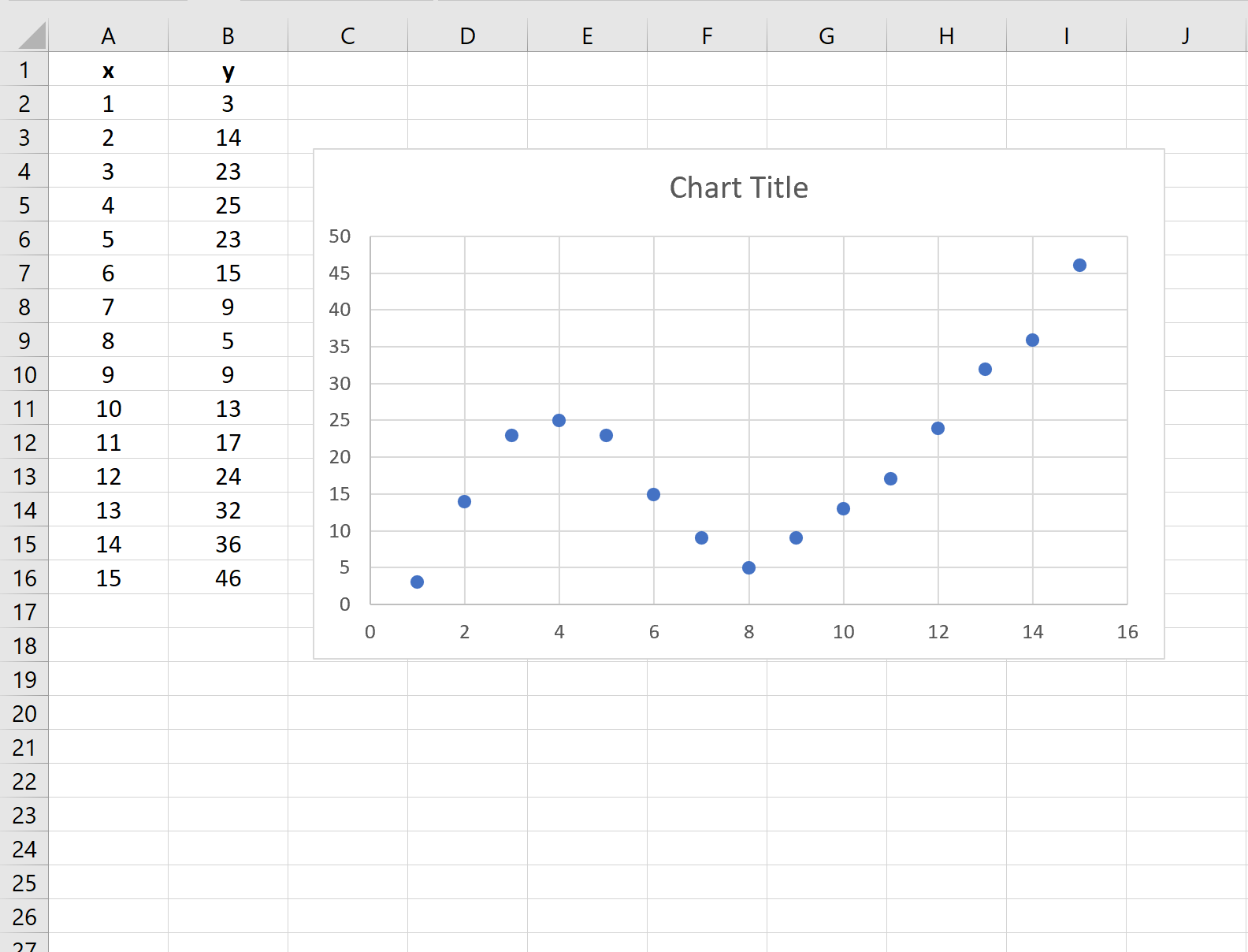
Schritt 3: Fügen Sie eine Trendlinie hinzu

Klicken Sie anschließend irgendwo auf das Streudiagramm. Klicken Sie dann auf das + -Zeichen in der oberen rechten Ecke. Klicken Sie im Dropdown-Menü auf den Pfeil neben „Trendlinie“ und dann auf „Weitere Optionen“ :

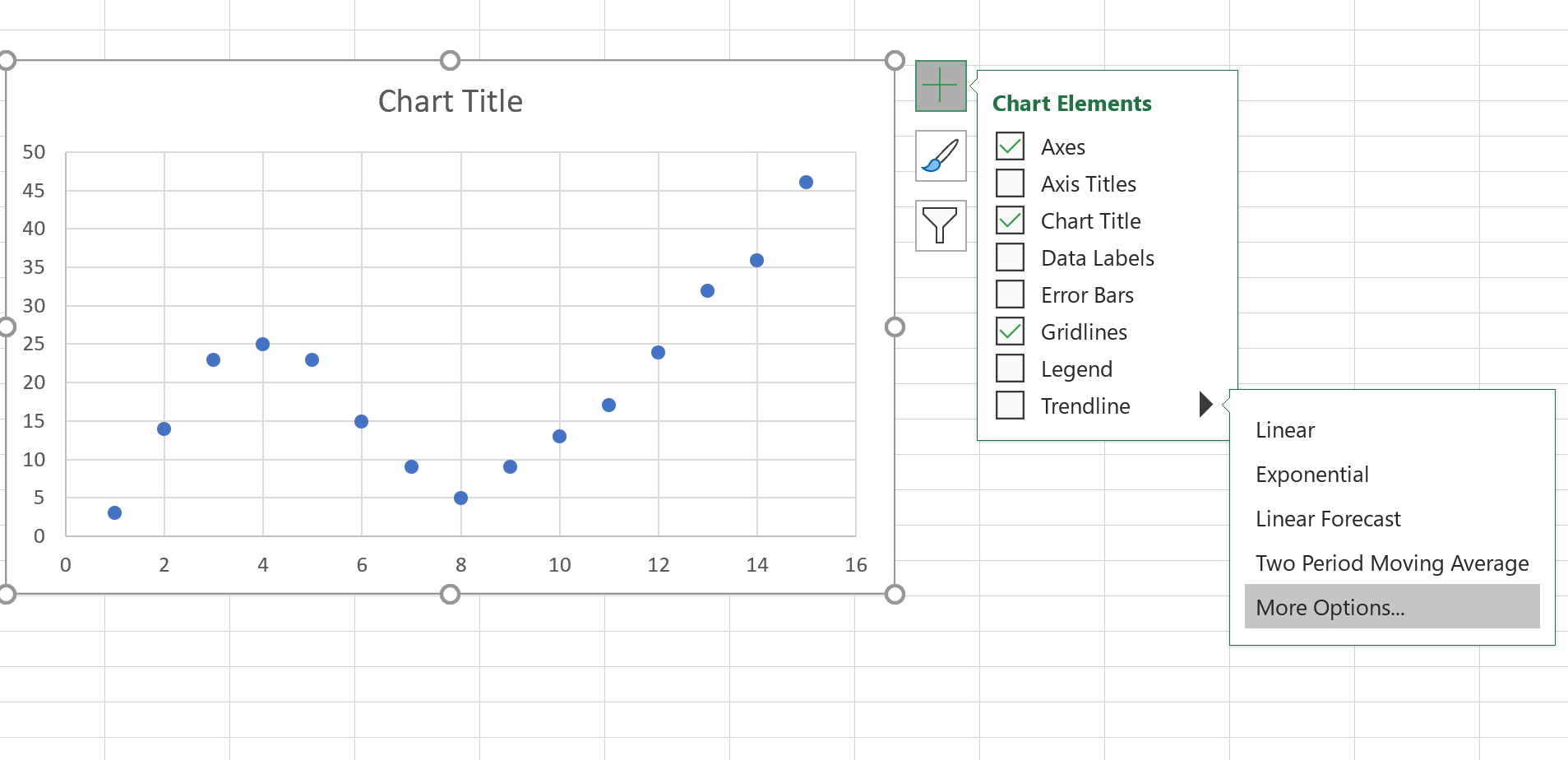
Klicken Sie im rechts angezeigten Fenster auf die Schaltfläche neben Polynom . Aktivieren Sie dann die Kontrollkästchen neben Gleichung im Diagramm anzeigen und R-Quadrat-Wert im Diagramm anzeigen .

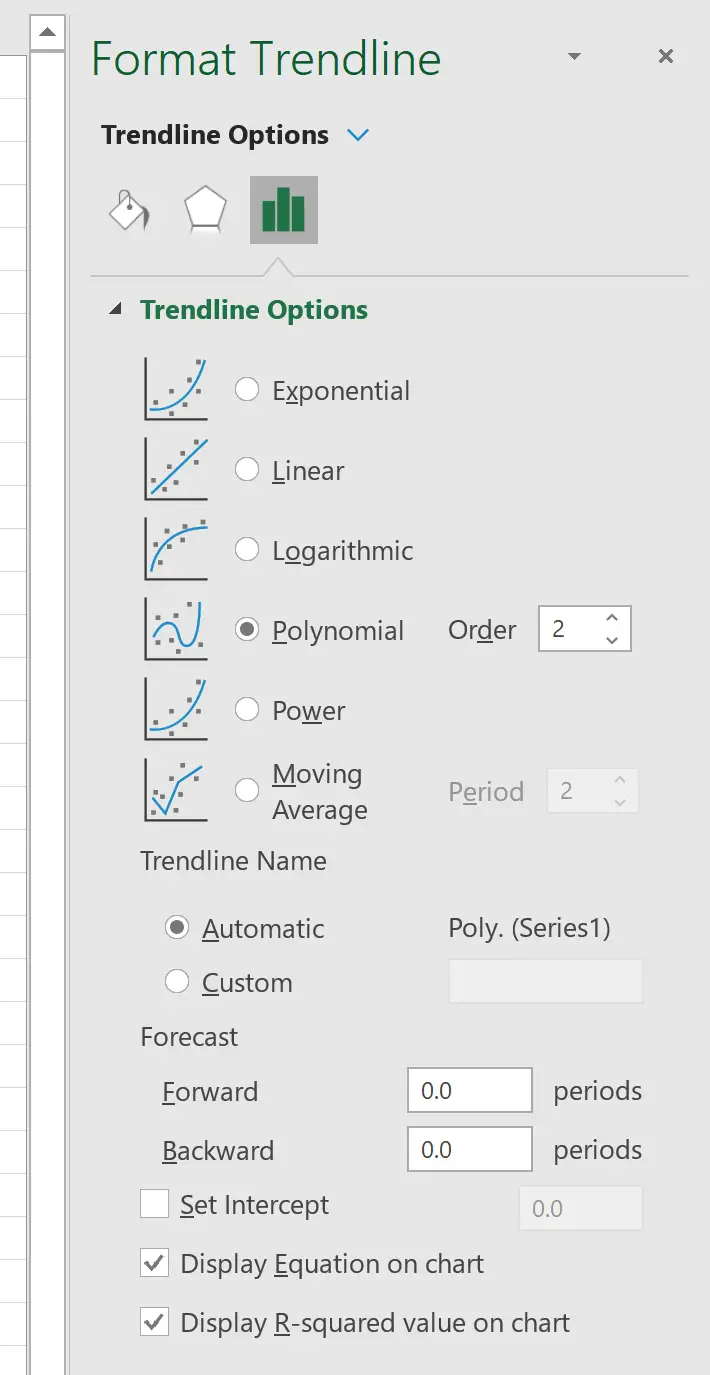
Dadurch entsteht auf der Punktwolke folgende Kurve:

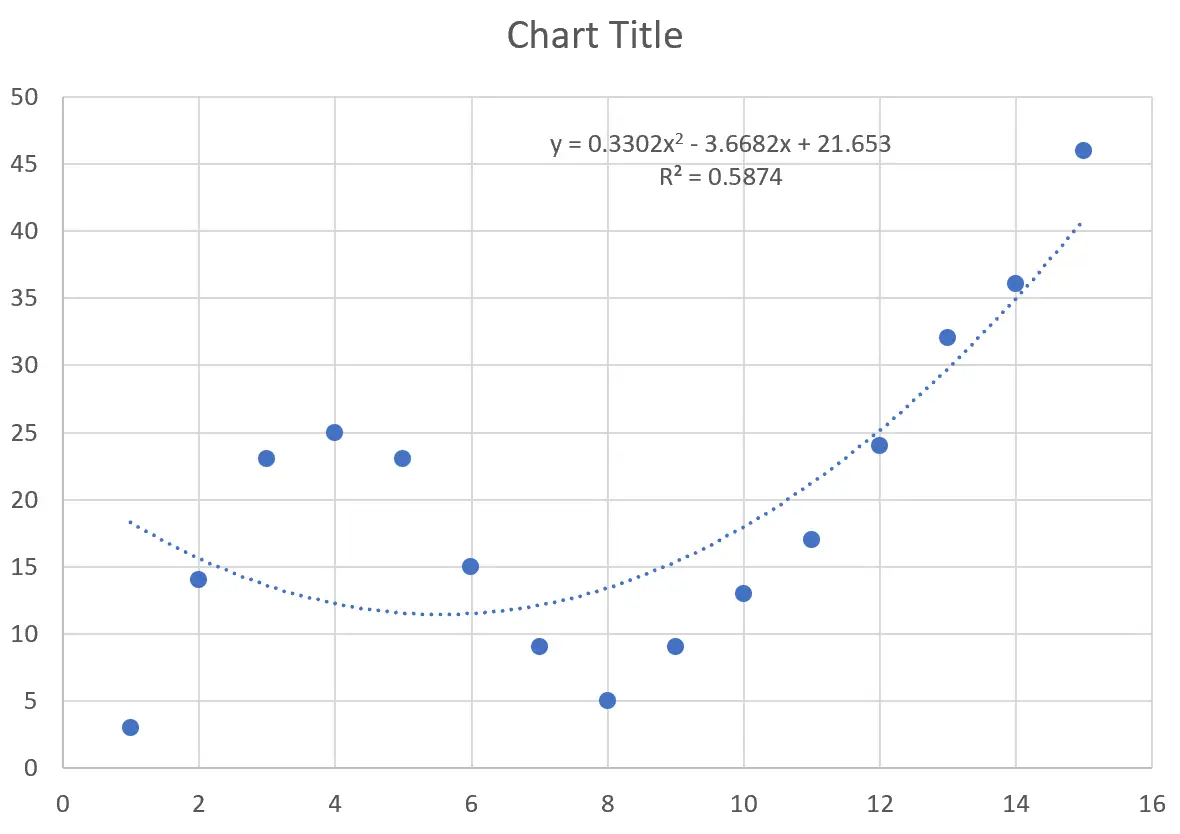
Die Gleichung der Kurve lautet wie folgt:

y = 0,3302x ² – 3,6682x + 21,653

Das R-Quadrat gibt uns den Prozentsatz der Variation in der Antwortvariablen an, der durch die Prädiktorvariablen erklärt werden kann. Das R-Quadrat für diese bestimmte Kurve beträgt 0,5874 .

Schritt 4: Wählen Sie die beste Trendlinie

Wir können auch die Ordnung des von uns verwendeten Polynoms erhöhen, um zu sehen, ob eine flexiblere Kurve besser zum Datensatz passt.

Beispielsweise könnten wir die Polynomordnung auf 4 festlegen:

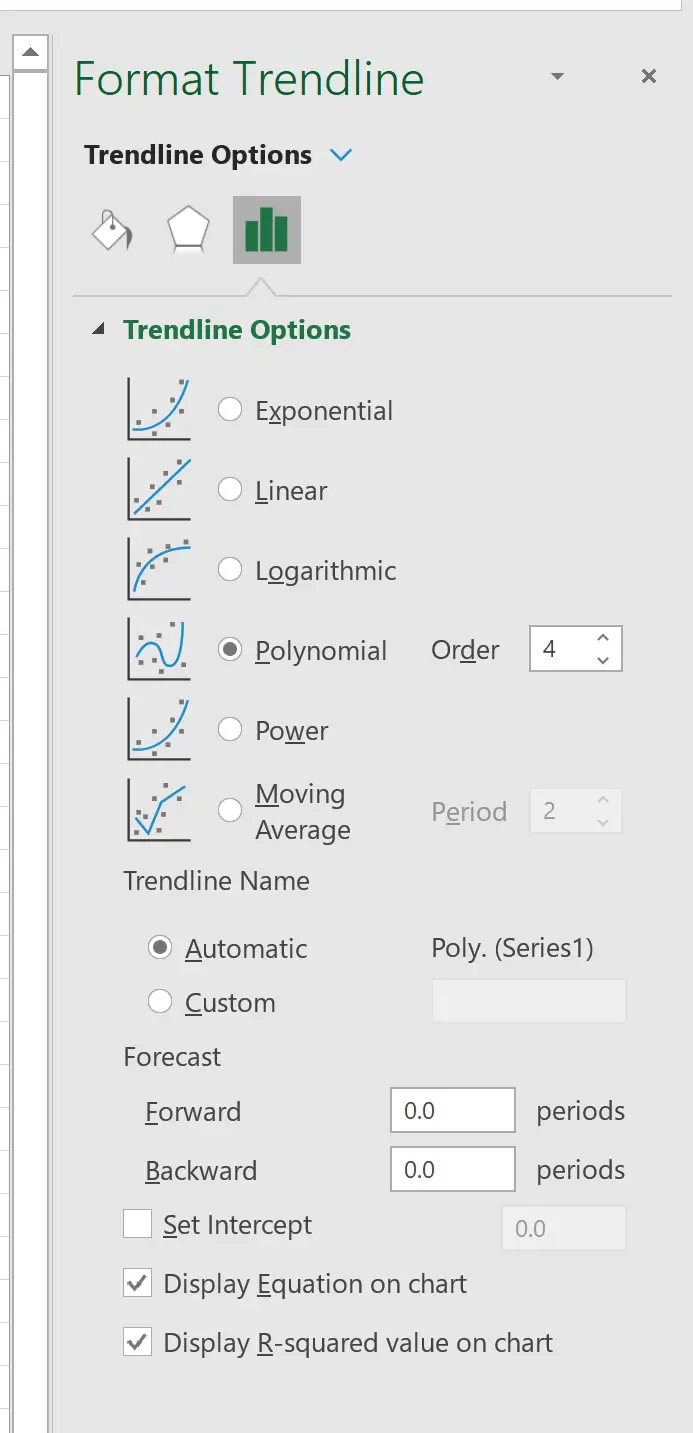
Daraus ergibt sich folgende Kurve:

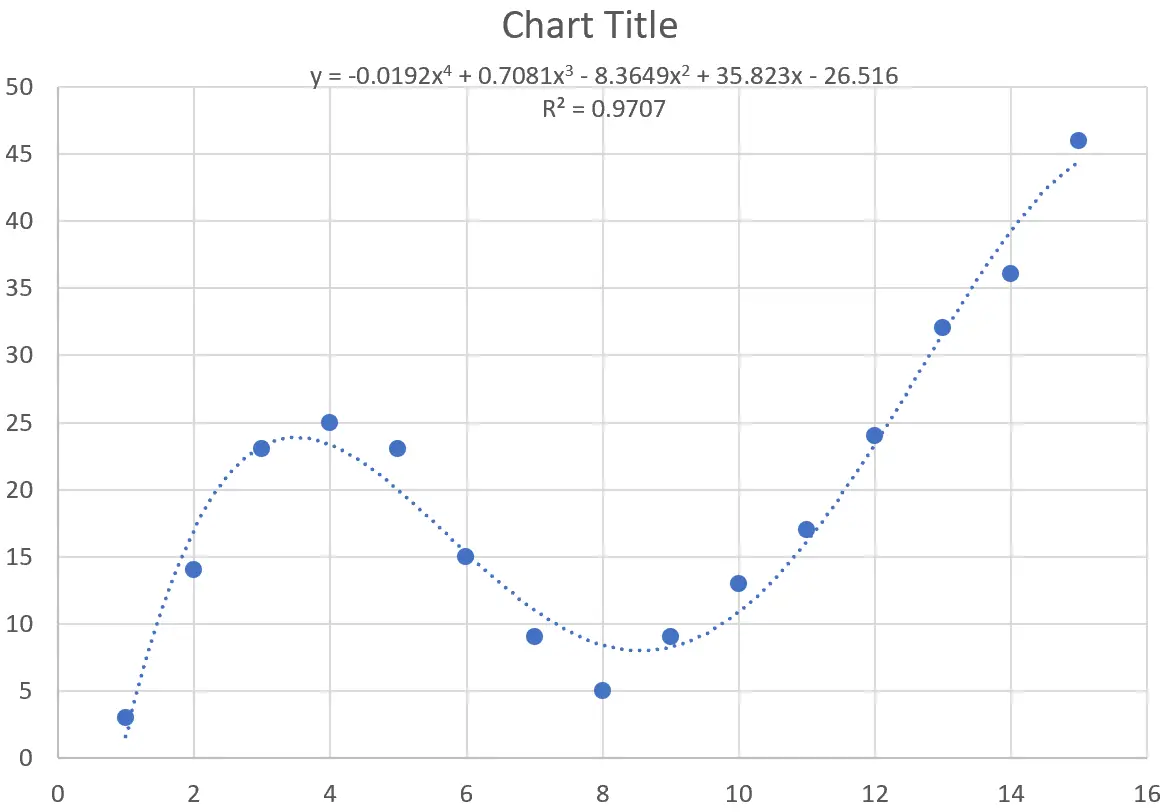
Die Gleichung der Kurve lautet wie folgt:

y = -0,0192x ⁴ + 0,7081x ³ – 8,3649x ² + 35,823x – 26,516

Das R-Quadrat für diese spezielle Kurve beträgt 0,9707 .

Dieses R-Quadrat ist erheblich höher als das der vorherigen Kurve, was darauf hindeutet, dass es viel besser mit dem Datensatz übereinstimmt.

Wir können diese Kurvengleichung auch verwenden, um den Wert der Antwortvariablen basierend auf der Prädiktorvariablen vorherzusagen. Wenn zum Beispiel x = 4, dann würden wir y = 23,34 vorhersagen:

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,3649(4) ² + 35,823(4) – 26,516 = 23,34

Weitere Excel-Tutorials finden Sie auf dieser Seite .